Date: June 27th, 2004
This chapter has three aims. First it shows how character table automorphisms can be utilized to construct certain character tables from others using the GAP system [GAP24]; the GAP functions used for that are part of the GAP Character Table Library [Bre25]. Second it documents several constructions of character tables which are contained in the GAP Character Table Library. Third it serves as a testfile for the involved GAP functions.
Several types of constructions of character tables of finite groups from known tables of smaller groups are described in Section 2.3. Selecting suitable character table automorphisms is an important ingredient of these constructions.
Section 2.2 collects the few representation theoretical facts on which these constructions are based.
The remaining sections show examples of the constructions in GAP. These examples use the GAP Character Table Library, therefore we load this package first.
gap> LoadPackage( "ctbllib", "1.1.4", false ); true
Let \(G\) be a finite group, \(Irr(G)\) be the matrix of ordinary irreducible characters of \(G\), \(Cl(G)\) be the set of conjugacy classes of elements in \(G\), \(g^G\) the \(G\)-conjugacy class of \(g \in G\), and let
\[ pow_p \colon Cl(G) \rightarrow Cl(G), g^G \mapsto (g^p)^G \]
be the \(p\)-th power map, for each prime integer \(p\).
A table automorphism of \(G\) is a permutation \(\sigma \colon Cl(G) \rightarrow Cl(G)\) with the properties that \(\chi \circ \sigma \in Irr(G)\) holds for all \(\chi \in Irr(G)\) and that \(\sigma\) commutes with \(pow_p\), for all prime integers \(p\) that divide the order of \(G\). Note that for prime integers \(p\) that are coprime to the order of \(G\), \(pow_p\) commutes with each \(\sigma\) that permutes \(Irr(G)\), since \(pow_p\) acts as a field automorphism on the character values.
In GAP, a character table covers the irreducible characters –a matrix \(M\) of character values– as well as the power maps of the underlying group –each power map \(pow_p\) being represented as a list \(pow_p^{\prime}\) of positive integers denoting the positions of the image classes. The group of table automorphisms of a character table is represented as a permutation group on the column positions of the table; it can be computed with the GAP function AutomorphismsOfTable (Reference: AutomorphismsOfTable).
In the following, we will mainly use that each group automorphism \(\sigma\) of \(G\) induces a table automorphism that maps the class of each element in \(G\) to the class of its image under \(\sigma\).
Two character tables with matrices \(M_1\), \(M_2\) of irreducibles and \(p\)-th power maps \(pow_{{1,p}}\), \(pow_{{2,p}}\) are permutation equivalent if permutations \(\psi\) and \(\pi\) of row and column positions of the \(M_i\) exist such that \([ M_1 ]_{{i,j}} = [ M_2 ]_{{i \psi, j \pi}}\) holds for all indices \(i\), \(j\), and such that \(\pi \cdot pow_{{2,p}}^{\prime} = pow_{{1,p}}^{\prime} \cdot \pi\) holds for all primes \(p\) that divide the (common) group order. The first condition is equivalent to the existence of a permutation \(\pi\) such that permuting the columns of \(M_1\) with \(\pi\) maps the set of rows of \(M_1\) to the set of rows of \(M_2\).
\(\pi\) is of course determined only up to table automorphisms of the two character tables, that is, two transforming permutations \(\pi_1\), \(\pi_2\) satisfy that \(\pi_1 \cdot \pi_2^{-1}\) is a table automorphism of the first table, and \(\pi_1^{-1} \cdot \pi_2\) is a table automorphism of the second.
Clearly two isomorphic groups have permutation equivalent character tables.
The GAP library function TransformingPermutationsCharacterTables (Reference: TransformingPermutationsCharacterTables) returns a record that contains transforming permutations of rows and columns if the two argument tables are permutation equivalent, and fail otherwise.
In the example sections, the following function for computing representatives from a list of character tables w.r.t. permutation equivalence will be used. More precisely, the input is either a list of character tables or a list of records which have a component table whose value is a character table, and the output is a sublist of the input.
gap> RepresentativesCharacterTables:= function( list ) > local reps, entry, r; > > reps:= []; > for entry in list do > if ForAll( reps, r -> ( IsCharacterTable( r ) and > TransformingPermutationsCharacterTables( entry, r ) = fail ) > or ( IsRecord( r ) and TransformingPermutationsCharacterTables( > entry.table, r.table ) = fail ) ) then > Add( reps, entry ); > fi; > od; > return reps; > end;;
For two groups \(H\), \(G\) such that \(H\) is isomorphic with a subgroup of \(G\), any embedding \(\iota \colon H \rightarrow G\) induces a class function
\[ fus_{\iota} \colon Cl(H) \rightarrow Cl(G), h^G \mapsto (\iota(h))^G \]
the class fusion of \(H\) in \(G\) via \(\iota\). Analogously, for a normal subgroup \(N\) of \(G\), any epimorphism \(\pi \colon G \rightarrow G/N\) induces a class function
\[ fus_{\pi} \colon Cl(G) \rightarrow Cl(G/N), g^G \mapsto (\pi(g))^G \]
the class fusion of \(G\) onto \(G/N\) via \(\pi\).
When one works only with character tables and not with groups, these class fusions are the objects that describe subgroup and factor group relations between character tables. Technically, class fusions are necessary for restricting, inducing, and inflating characters from one character table to another. If one is faced with the problem to compute the class fusion between the character tables of two groups \(H\) and \(G\) for which it is known that \(H\) can be embedded into \(G\) then one can use character-theoretic necessary conditions, concerning that the restriction of all irreducible characters of \(G\) to \(H\) (via the class fusion) must decompose into the irreducible characters of \(H\), and that the class fusion must commute with the power maps of \(H\) and \(G\).
With this character-theoretic approach, one can clearly determine possible class fusions only up to character table automorphisms. Note that one can interpret each character table automorphism of \(G\) as a class fusion from the table of \(G\) to itself.
If \(N\) is a normal subgroup in \(G\) then the class fusion of \(N\) in \(G\) determines the orbits of the conjugation action of \(G\) on the classes of \(N\). Often the knowledge of these orbits suffices to identify the subgroup of table automorphisms of \(N\) that corresponds to this action of \(G\); for example, this is always the case if \(N\) has index \(2\) in \(G\).
GAP library functions for dealing with class fusions, power maps, and character table automorphisms are described in the chapter Maps Concerning Character Tables
in the GAP Reference Manual.
As is stated in [CCN+85, p. xxiii], two groups \(G\), \(H\) are called isoclinic if they can be embedded into a group \(K\) such that \(K\) is generated by \(Z(K)\) and \(G\), and also by \(Z(K)\) and \(H\). In the following, two special cases of isoclinism will be used, where the character tables of the isoclinic groups are closely related.
\(G \cong 2 \times U\) for a group \(U\) that has a central subgroup \(N\) of order \(2\), and \(H\) is the central product of \(U\) and a cyclic group of order four. Here we can set \(K = 2 \times H\).
\(G \cong 2 \times U\) for a group \(U\) that has a normal subgroup \(N\) of index \(2\), and \(H\) is the subdirect product of \(U\) and a cyclic group of order four, Here we can set \(K = 4 \times U\).

Starting from the group \(K\) containing both \(G\) and \(H\), we first note that each irreducible representation of \(G\) or \(H\) extends to \(K\). More specifically, if \(\rho_G\) is an irreducible representation of \(G\) then we can define an extension \(\rho\) of \(K\) by defining it suitably on \(Z(K)\) and then form \(\rho_H\), the restriction of \(\rho\) to \(H\).
In our two cases, we set \(S = G \cap H\), so \(K = S \cup G \setminus S \cup H \setminus S \cup z S\) holds for some element \(z \in Z(K) \setminus ( G \cup H )\) of order four, and \(G = S \cup g S\) for some \(g \in G \setminus S\), and \(H = S \cup h S\) where \(h = z \cdot g \in H \setminus S\). For defining \(\rho_H\), it suffices to consider \(\rho(h) = \rho(z) \rho(g)\), where \(\rho(z) = \epsilon_{\rho}(z) \cdot I\) is a scalar matrix.
As for the character table heads of \(G\) and \(H\), we have \(s^G = s^H\) and \(z (g \cdot s)^G = (h \cdot s)^H\) for each \(s \in S\), so this defines a bijection of the conjugacy classes of \(G\) and \(H\). For a prime integer \(p\), \((h \cdot s)^p = (z \cdot g \cdot s)^p = z^p \cdot (g \cdot s)^p\) holds for all \(s \in S\), so the \(p\)-th power maps of \(G\) and \(H\) are related as follows: Inside \(S\) they coincide for any \(p\). If \(p \equiv 1 \bmod 4\) they coincide also outside \(S\), if \(p \equiv -1 \bmod 4\) the images differ by exchanging the classes of \((h \cdot s)^p\) and \(z^2 \cdot (h \cdot s)^p\) (if these elements lie in different classes), and for \(p = 2\) the images (which lie inside \(S\)) differ by exchanging the classes of \((h \cdot s)^2\) and \(z^2 \cdot (g \cdot s)^2\) (if these elements lie in different classes).
Let \(\rho\) be an irreducible representation of \(K\). Then \(\rho_G\) and \(\rho_H\) are related as follows: \(\rho_G(s) = \rho_H(s)\) and \(\rho(z) \cdot \rho_G(g \cdot s) = \rho_H(h \cdot s)\) for all \(s \in S\). If \(\chi_G\) and \(\chi_H\) are the characters afforded by \(\rho_G\) and \(\rho_H\), respectively, then \(\chi_G(s) = \chi_H(s)\) and \(\epsilon_{\rho}(z) \cdot \chi_G(g \cdot s) = \chi_H(h \cdot s)\) hold for all \(s \in S\). In the case \(\chi_G(z^2) = \chi(1)\) we have \(\epsilon_{\rho}(z) = \pm 1\), and both cases actually occur if one considers all irreducible representations of \(K\). In the case \(\chi_G(z^2) = - \chi(1)\) we have \(\epsilon_{\rho}(z) = \pm i\), and again both cases occur. So we obtain the irreducible characters of \(H\) from those of \(G\) by multiplying the values outside \(S\) in all those characters by \(i\) that do not have \(z^2\) in their kernels.
In GAP, the function CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) can be used for computing the character table of \(H\) from that of \(G\), and vice versa. (Note that in the above two cases, also the groups \(U\) and \(H\) are isoclinic by definition, but CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) does not transfer the character table of \(U\) to that of \(H\).)
One could construct the character tables mentioned above by forming the character tables of certain factor groups or normal subgroups of direct products. However, the construction via CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) has the advantage that the result stores from which sources it arose, and this information can be used to derive also the Brauer character tables, provided that the Brauer character tables of the source tables are known.
Since the release of GAP 4.11, CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) admits the construction of the character tables of the isoclinic variants of groups of the structure \(p.G.p\), also for odd primes \(p\).
This feature will be used in the construction of the character table of \(9.U_3(8).3_3\), in order to construct the table of the subgroup \(3.(3 \times U_3(8))\) and of the factor group \((3 \times U_3(8)).3_3\), see Section 2.4-16. These constructions are a straightforward generalization of those described in detail in Section 2.2-4.
There are several examples of Atlas groups of the structure \(3.G.3\). The character table of one such group is shown in the Atlas, the tables of their isoclinic variants can now be obtained from CharacterTableIsoclinic (Reference: CharacterTableIsoclinic).
For example, the group GL\((3,4)\) has the structure \(3.L_3(4).3\). There are three pairwise nonisomorphic isoclinic variants of groups of this structure.
gap> t:= CharacterTable( "3.L3(4).3" ); CharacterTable( "3.L3(4).3" ) gap> iso1:= CharacterTableIsoclinic( t ); CharacterTable( "Isoclinic(3.L3(4).3,1)" ) gap> iso2:= CharacterTableIsoclinic( t, rec( k:= 2 ) ); CharacterTable( "Isoclinic(3.L3(4).3,2)" ) gap> TransformingPermutationsCharacterTables( t, iso1 ); fail gap> TransformingPermutationsCharacterTables( t, iso2 ); fail gap> TransformingPermutationsCharacterTables( iso1, iso2 ); fail
The character table of GL\((3,4)\) is in fact the one which is shown in the Atlas.
gap> IsRecord( TransformingPermutationsCharacterTables( t, > CharacterTable( GL( 3, 4 ) ) ) ); true
The function CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) can also be used to switch between the character tables of double covers of groups of the type \(G.2\), where \(G\) is a perfect group, see [CCN+85, Section 6.7]. Typical examples are the double covers of symmetric groups.
Note that these double covers may be isomorphic. This happens for \(2.S_6\). More generally, this happens for all semilinear groups \(\Sigma\)L\((2,p^2)\), for odd primes \(p\). The smallest examples are \(\Sigma\)L\((2,9) = 2.A_6.2_1\) and \(\Sigma\)L\((2,25) = 2.L_2(25).2_2\). This implies that the character table and its isoclinic variant are permutation isomorphic.
gap> t:= CharacterTable( "2.A6.2_1" ); CharacterTable( "2.A6.2_1" ) gap> TransformingPermutationsCharacterTables( t, > CharacterTableIsoclinic( t ) ); rec( columns := (4,6)(5,7)(11,12)(14,16)(15,17), group := Group([ (16,17), (14,15) ]), rows := (3,5)(4,6)(10,11)(12,15,13,14) ) gap> t:= CharacterTable( "2.L2(25).2_2" ); CharacterTable( "2.L2(25).2_2" ) gap> TransformingPermutationsCharacterTables( t, > CharacterTableIsoclinic( t ) ); rec( columns := (7,9)(8,10)(20,21)(23,24)(25,27)(26,28), group := <permutation group with 4 generators>, rows := (3,5)(4,6)(14,15)(16,17)(19,22,20,21) )
For groups of the type \(4.G.2\), two different situations can occur. Either the distinguished central cyclic subgroup of order four in \(4.G\) is inverted by the elements in \(4.G.2 \setminus 4.G\), or this subgroup is central in \(4.G.2\). In the first case, calling CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) with the character table of \(4.G.2\) yields a character table with the same set of irreducibles, only the \(2\)-power map will in general differ from that of the input table. In the second case, the one argument version of CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) returns a permutation isomorphic table. By supplying additional arguments, there is a chance to construct tables of different groups.
We demonstrate this phenomenon with the various groups of the structure \(4.L_3(4).2\).
gap> tbls:= [];; gap> for m in [ "4_1", "4_2" ] do > for a in [ "2_1", "2_2", "2_3" ] do > Add( tbls, CharacterTable( Concatenation( m, ".L3(4).", a ) ) ); > od; > od; gap> tbls; [ CharacterTable( "4_1.L3(4).2_1" ), CharacterTable( "4_1.L3(4).2_2" ) , CharacterTable( "4_1.L3(4).2_3" ), CharacterTable( "4_2.L3(4).2_1" ), CharacterTable( "4_2.L3(4).2_2" ) , CharacterTable( "4_2.L3(4).2_3" ) ] gap> case1:= Filtered( tbls, t -> Size( ClassPositionsOfCentre( t ) ) = 2 ); [ CharacterTable( "4_1.L3(4).2_1" ), CharacterTable( "4_1.L3(4).2_2" ) , CharacterTable( "4_2.L3(4).2_1" ), CharacterTable( "4_2.L3(4).2_3" ) ] gap> case2:= Filtered( tbls, t -> Size( ClassPositionsOfCentre( t ) ) = 4 ); [ CharacterTable( "4_1.L3(4).2_3" ), CharacterTable( "4_2.L3(4).2_2" ) ]
The centres of the groups \(4_1.L_3(4).2_1\), \(4_1.L_3(4).2_2\), \(4_2.L_3(4).2_1\), and \(4_2.L_3(4).2_3\) have order two, that is, these groups belong to the first case. Each of these groups is not permutation equivalent to its isoclinic variant but has the same irreducible characters.
gap> isos1:= List( case1, CharacterTableIsoclinic );; gap> List( [ 1 .. 4 ], i -> Irr( case1[i] ) = Irr( isos1[i] ) ); [ true, true, true, true ] gap> List( [ 1 .. 4 ], > i -> TransformingPermutationsCharacterTables( case1[i], isos1[i] ) ); [ fail, fail, fail, fail ]
The groups \(4_1.L_3(4).2_3\) and \(4_2.L_3(4).2_2\) belong to the second case because their centres have order four.
gap> isos2:= List( case2, CharacterTableIsoclinic );; gap> List( [ 1, 2 ], > i -> TransformingPermutationsCharacterTables( case2[i], isos2[i] ) ); [ rec( columns := (26,27,28,29)(30,31,32,33)(38,39,40,41)(42,43,44,45) , group := <permutation group with 5 generators>, rows := (16,17)(18,19)(20,21)(22,23)(28,29)(32,33)(36,37)(40, 41) ), rec( columns := (28,29,30,31)(32,33)(34,35,36,37)(38,39,40,41)(42, 43,44,45)(46,47,48,49), group := <permutation group with 3 generators>, rows := (15,16)(17,18)(20,21)(22,23)(24,25)(26, 27)(28,29)(34,35)(38,39)(42,43)(46,47) ) ] gap> isos3:= List( case2, t -> CharacterTableIsoclinic( t, > ClassPositionsOfCentre( t ) ) );; gap> List( [ 1, 2 ], > i -> TransformingPermutationsCharacterTables( case2[i], isos3[i] ) ); [ fail, fail ]
Let \(G\) be a group and \(N\) be a normal subgroup of \(G\). We will need the following well-known facts about the relation between the irreducible characters of \(G\) and \(N\).
For an irreducible (Brauer) character \(\chi\) of \(N\) and \(g \in G\), we define \(\chi^g\) by \(\chi^g(n) = \chi(n^g)\) for all \(n \in N\), and set \(I_G(\chi) = \{ g \in G; \chi^g = \chi \}\) (see [Fei82, p. 86]).
If \(I_G(\chi) = N\) then the induced character \(\chi^G\) is an irreducible (Brauer) character of \(G\) (see [Fei82, Lemma III 2.11] or [Nav98, Theorem 8.9] or [LP10, Corollary 4.3.8]).
If \(G/N\) is cyclic and if \(I_G(\chi) = G\) then \(\chi = \psi_N\) for an irreducible (Brauer) character \(\psi\) of \(G\), and each irreducible (Brauer) character \(\theta\) with the property \(\chi = \theta_N\) is of the form \(\theta = \psi \cdot \epsilon\), where \(\epsilon\) is an irreducible (Brauer) character of \(G/N\) (see [Fei82, Theorem III 2.14] or [Nav98, Theorem 8.12] or [LP10, Theorem 3.6.13]).
Clifford's theorem ([Fei82, Theorem III 2.12] or [Nav98, Corollary 8.7] or [LP10, Theorem 3.6.2]) states that the restriction of an irreducible (Brauer) character of \(G\) to \(N\) has the form \(e \sum_{i=1}^t \varphi_i\) for a positive integer \(e\) and irreducible (Brauer) characters \(\varphi_i\) of \(N\), where \(t\) is the index of \(I_G(\varphi_1)\) in \(G\).
Now assume that \(G\) is a normal subgroup in a larger group \(H\), that \(G/N\) is an abelian chief factor of \(H\) and that \(\psi\) is an ordinary irreducible character of \(G\) such that \(I_H(\psi) = H\). Then either \(t = 1\) and \(e^2\) is one of \(1\), \(|G/N|\), or \(t = |G/N|\) and \(e = 1\) (see [Isa76, Theorem 6.18]).
(This kind of table construction is described in [Bre11].)
Let \(N\) denote a downward extension of the finite group \(G\) by a finite group \(M\), let \(H\) denote an automorphic (upward) extension of \(N\) by a finite cyclic group \(A\) such that \(M\) is normal in \(H\), and set \(F = H / M\). We consider the situation that each irreducible character of \(N\) that does not contain \(M\) in its kernel induces irreducibly to \(H\). Equivalently, the action of \(A = \langle a \rangle\) on the characters of \(N\), via \(\chi \mapsto \chi^a\), has only orbits of length exactly \(|A|\) on the set \(\{ \chi \in Irr(N); M \nsubseteq \ker(\chi) \}\).
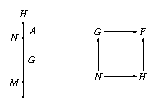
This occurs for example if \(M\) is central in \(N\) and \(A\) acts fixed-point freely on \(M\), we have \(|M| \equiv 1 \bmod |A|\) in this case. If \(M\) has prime order then it is sufficient that \(A\) does not centralize \(M\).
The ordinary (or \(p\)-modular) irreducible characters of \(H\) are then given by the ordinary (or \(p\)-modular) irreducible characters of \(F\) and \(N\), the class fusions from the table of \(N\) onto the table of \(G\) and from the table of \(G\) into that of \(F\), and the permutation \(\pi\) that is induced by the action of \(A\) on the conjugacy classes of \(N\).
In general, the action of \(A\) on the classes of \(M\) is not the right thing to look at, one really must consider the action on the relevant characters of \(M.G\). For example, take \(H\) the quaternion group or the dihedral group of order eight, \(N\) a cyclic subgroup of index two, and \(M\) the centre of \(H\); here \(A\) acts trivially on \(M\), but the relevant fact is that the action of \(A\) swaps those two irreducible characters of \(N\) that take the value \(-1\) on the involution in \(M\) –these are the faithful irreducible characters of \(N\).
If the orders of \(M\) and \(A\) are coprime then also the power maps of \(H\) can be computed from the above data. For each prime \(p\) that divides the orders of both \(M\) and \(A\), the \(p\)-th power map is in general not uniquely determined by these input data. In this case, we can compute the (finitely many) candidates for the character table of \(H\) that are described by these data. One possible reason for ambiguities is the existence of several isoclinic but nonisomorphic groups that can arise from the input tables (cf. Section 2.2-4, see Section 2.4-12 for an example).
With the GAP function PossibleActionsForTypeMGA (CTblLib: PossibleActionsForTypeMGA), one can compute the possible orbit structures induced by \(G.A\) on the classes of \(M.G\), and PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) computes the possible ordinary character tables for a given orbit structure. For constructing the \(p\)-modular Brauer table of a group \(H\) of the structure \(M.G.A\), the GAP function BrauerTableOfTypeMGA (CTblLib: BrauerTableOfTypeMGA) takes the ordinary character table of \(H\) and the \(p\)-modular tables of the subgroup \(M.G\) and the factor group \(G.A\) as its input. The \(p\)-modular table of \(G\) is not explicitly needed in the construction, it is implicitly given by the class fusions from \(M.G\) into \(M.G.A\) and from \(M.G.A\) onto \(G.A\); these class fusions must of course be available.
The GAP Character Table Library contains many tables of groups of the structure \(M.G.A\) as described above, which are encoded by references to the tables of the groups \(M.G\) and \(G.A\), plus the fusion and action information. This reduces the space needed for storing these character tables.
For examples, see Section 2.4.
Let \(G\) be a finite group, and \(H\) be an upward extension of \(G\) such that the factor group \(H / G\) is a Frobenius group \(F = K C\) with abelian kernel \(K\) and cyclic complement \(C\) of prime order \(c\). (Typical cases for \(F\) are the symmetric group \(S_3\) on three points and the alternating group \(A_4\) on four points.) Let \(N\) and \(U\) denote the preimages of \(K\) and \(C\) under the natural epimorphism from \(H\) onto \(F\).
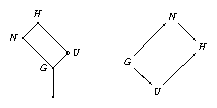
For certain isomorphism types of \(F\), the ordinary (or \(p\)-modular) character table of \(H\) can be computed from the ordinary (or \(p\)-modular) character tables of \(G\), \(U\), and \(N\), the class fusions from the table of \(G\) into those of \(U\) and \(N\), and the permutation \(\pi\) induced by \(H\) on the conjugacy classes of \(N\). This holds for example for \(F = S_3\) and in the ordinary case also for \(F = A_4\).
Each class of \(H\) is either a union of \(\pi\)-orbits or an \(H\)-class of \(U \setminus G\); the latter classes are in bijection with the \(U\)-classes of \(U \setminus G\), they are just \(|K|\) times larger since the \(|K|\) conjugates of \(U\) in \(H\) are fused. The power maps of \(H\) are uniquely determined from the power maps of \(U\) and \(N\), because each element in \(F\) lies in \(K\) or in an \(F\)-conjugate of \(C\).
Concerning the computation of the ordinary irreducible characters of \(H\), we could induce the irreducible characters of \(U\) and \(N\) to \(H\), and then take the union of the irreducible characters among those and the irreducible differences of those. (For the case \(F = S_3\), this approach has been described in the Appendix of [HL94].)
The GAP function CharacterTableOfTypeGS3 (CTblLib: CharacterTableOfTypeGS3) proceeds in a different way, which is suitable also for the construction of \(p\)-modular character tables of \(H\).
By the facts listed in Section 2.2-7, for an irreducible (Brauer) character \(\chi\) of \(N\), we have \(I_H(\chi)\) equal to either \(N\) or \(H\). In the former case, \(\chi\) induces irreducibly to \(H\). In the latter case, there are extensions \(\psi^{(i)}\), \(1 \leq i \leq |C|\) (or \(|C|_{p^\prime}\)), to \(H\), and we have the following possibilities, depending on the restriction \(\chi_G\).
If \(\chi_G = e \varphi\), for an irreducible character \(\varphi\) of \(G\), then \(I_U(\varphi) = U\) holds, hence the \(\psi^{(i)}_U\) are \(|C|\) (or \(|C|_{p^\prime}\)) extensions of \(\chi_G\) to \(U\). Moreover, we have either \(e = 1\) or \(e^2 = |K|\). In the case \(e = 1\), this determines the values of the \(\psi^{(i)}\) on the classes of \(U\) outside \(G\). In the case \(e ≠ 1\), we have the problem to combine \(e\) extensions of \(\varphi\) to a character of \(U\) that extends to \(H\).
(One additional piece of information in the case of ordinary character tables is that the norm of this linear combination equals \(1 + (|K|-1)/|C|\), which determines the \(\psi^{(i)}_U\) if \(F = A_4 \cong 2^2:3\) or \(F = 2^3:7\) holds; in the former case, the sum of each two out of the three different extensions of \(\varphi\) extends to \(U\); in the latter case, the sum of all different extensions plus one of the extensions extends. Note that for \(F = S_3\), the case \(e ≠ 1\) does not occur.)
The remaining case is that \(\chi_G\) is not a multiple of an irreducible character of \(G\). Then \(\chi_G = \varphi_1 + \varphi_2 + \ldots + \varphi_{|K|}\), for pairwise different irreducible characters \(\varphi_i\), \(1 \leq i \leq |K|\), of \(G\) with the property \(\varphi_i^N = \chi\). The action of \(U\) on \(G\) fixes at least one of the \(\varphi_i\), since \(|K| \equiv 1 \bmod |C|\). Without loss of generality, let \(I_U(\varphi_1) = U\), and let \(\varphi_1^{(i)}\), \(1 \leq i \leq |C|\), be the extensions of \(\varphi_1\) to \(U\). (In fact exactly \(\varphi_1\) is fixed by \(U\) since otherwise \(k \in K\) would exist with \(\varphi_1^k ≠ \varphi_1\) and such that also \(\varphi_1^k\) would be invariant in \(U\); but then \(\varphi_1\) would be invariant under both \(C\) and \(C^k\), which generate \(F\). So each of the \(|K|\) constituents is invariant in exactly one of the \(|K|\) subgroups of type \(U\) above \(G\).)
Then \(((\varphi_1^{(i)})^H)_N = \varphi_1^N = \chi\), hence the values of \(\psi^{(i)}\) on the classes of \(U \setminus G\) are given by those of \((\varphi_1^{(i)})^H\). (These are exactly the values of \(\varphi_1^{(i)}\). So in both cases, we take the values of \(\chi\) on \(N\), and on the classes of \(U \setminus G\) the values of the extensions of the unique extendible constituent of \(\chi_G\).)
For examples, see Section 2.5.
Let \(G\) be a finite group, and \(H\) be an upward extension of \(G\) such that the factor group \(H / G\) is a Klein four group. We assume that the ordinary character tables of \(G\) and of the three index two subgroups \(U_1\), \(U_2\), and \(U_3\) (of the structures \(G.2_1\), \(G.2_2\), and \(G.2_3\), respectively) of \(H\) above \(G\) are known, as well as the class fusions of \(G\) into these groups. The idea behind the method that is described in this section is that in this situation, there are only few possibilities for the ordinary character table of \(H\).
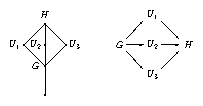
Namely, the action of \(H\) on the classes of \(G.2_i\) is given by a table automorphism \(\pi_i\) of \(G.2_i\), and \(H\) realizes compatible choices of such automorphisms \(\pi_1\), \(\pi_2\), \(\pi_3\) in the sense that the orbits of all three \(\pi_i\) on the classes of \(G\) inside the groups \(G.2_i\) coincide. Furthermore, if \(G.2_i\) has \(n_i\) conjugacy classes then an action \(\pi_i\) that is a product of \(f_i\) disjoint transpositions leads to a character table candidate for \(G.2^2\) that has \(2 n_i - 3 f_i\) classes, so also the \(f_i\) must be compatible.
Taking the inner
classes, i.e., the orbit sums of the classes inside \(G\) under the \(\pi_i\), plus the union of the \(\pi_i\)-orbits of the classes of \(G.2_i \setminus G\) gives a possibility for the classes of \(H\). Furthermore, the power maps of the groups \(G.2_i\) determine the power maps of the candidate table constructed this way.
Concerning the computation of the irreducible characters of \(H\), we consider also the case of \(p\)-modular characters tables, where we assume that the ordinary character table of \(H\) is already known and the only task is to compute the irreducible \(p\)-modular Brauer characters.
Let \(\chi\) be an irreducible (\(p\)-modular Brauer) character of \(G\). By the facts that are listed in Section 2.2-7, there are three possibilities.
\(I_H(\chi) = G\); then \(\chi^H\) is irreducible.
\(I_H(\chi) = G.2_i\) for \(i\) one of \(1\), \(2\), \(3\); then \(I_{G.2_i}(\chi) = G.2_i\) for this \(i\), so \(\chi\) extends to \(G.2_i\); none of these extensions extends to \(H\) (because otherwise \(\chi\) would be invariant in \(H\)), so they induce irreducible characters of \(H\).
\(I_H(\chi) = H\); then \(\chi\) extends to each of the three groups \(G.2_i\), and either all these extensions induce the same character of \(H\) (which vanishes on \(H \setminus G\)) or they are invariant in \(H\) and thus extend to \(H\).
In the latter part of case 3. (except if \(p = 2\)), the problem is to combine the values of six irreducible characters of the groups \(G.2_i\) to four characters of \(H\). This yields essentially two choices, and we try to exclude one possibility by forming scalar products with the \(2\)-nd symmetrizations of the known irreducibles. If several possibilities remain then we get several possible tables.
So we end up with a list of possible character tables of \(H\). The first step is to specify a list of possible triples \((\pi_1, \pi_2, \pi_3)\), using the table automorphisms of the groups \(G.2_i\); this can be done using the GAP function PossibleActionsForTypeGV4 (CTblLib: PossibleActionsForTypeGV4). Then the GAP function PossibleCharacterTablesOfTypeGV4 (CTblLib: PossibleCharacterTablesOfTypeGV4) can be used for computing the character table candidates for each given triple of permutations; it may of course happen that some triples of automorphisms are excluded in this second step.
For examples, see Section 2.6.
Let \(G\) be a finite group, and \(H\) be a central extension of \(G\) by a Klein four group \(Z = \langle z_1, z_2 \rangle\); set \(z_3 = z_1 z_2\) and \(Z_i = \langle z_i \rangle\), for \(1 \leq i \leq 3\). We assume that the ordinary character tables of the three factor groups \(2_i.G = H / Z_i\) of \(H\) are known, as well as the class fusions from these groups to \(G\). The idea behind the method described in this section is that in this situation, there are only few possibilities for the ordinary character table of \(H\).
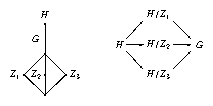
Namely, the irreducible (\(p\)-modular) characters of \(H\) are exactly the inflations of the irreducible (\(p\)-modular) characters of the three factor groups \(H / Z_i\). (Note that for any noncyclic central subgroup \(C\) of \(H\) and any \(\chi \in Irr(H)\), we have \(|\ker(\chi) \cap C| > 1\). To see this, let \(N = \ker(\chi)\). Then clearly \(|N| > 1\), and \(\chi\) can be regarded as a faithful irreducible character of \(H/N\). If \(N \cap C\) would be trivial then \(N C / N \cong C\) would be a noncyclic central subgroup of \(H/N\). This cannot happen by [Isa76, Thm. 2.32 (a)], so the statement can be regarded as an obvious refinement of this theorem.) So all we have to construct is the character table head of \(H\) –classes and power maps– and the factor fusions from \(H\) to these groups.
For fixed \(h \in H\), we consider the question in which \(H\)-classes the elements \(h\), \(h z_1\), \(h z_2\), and \(h z_3\) lie. There are three possibilities.
The four elements are all conjugate in \(H\). Then in each of the three groups \(H/Z_i\), the two preimages of \(h Z \in H/Z\) are conjugate.
We are not in case 1. but two of the four elements are conjugate in \(H\), i. e., \(g^{-1} h g = h z_i\) for some \(g \in H\) and some \(i\); then \(g^{-1} h z_j g = h z_i z_j\) for each \(j\), so the four elements lie in exactly two \(H\)-classes. This implies that for \(i ≠ j\), the elements \(h\) and \(h z_j\) are not \(H\)-conjugate, so \(h Z_i\) is not conjugate to \(h z_j Z_i\) in \(H/Z_i\) and \(h Z_j\) is conjugate to \(h z_i Z_j\) in \(H/Z_j\).
The four elements are pairwise nonconjugate in \(H\). Then in each of the three groups \(H/Z_i\), the two preimages of \(h Z \in H/Z\) are nonconjugate.
We observe that the question which case actually applies for \(h \in H\) can be decided from the three factor fusions from \(H/Z_i\) to \(G\). So we attempt to construct the table head of \(H\) and the three factor fusions from \(H\) to the groups \(H/Z_i\), as follows. Each class \(g^G\) of \(G\) yields either one or two or four preimage classes in \(H\).
In case 1., we get one preimage class in \(H\), and have no choice for the factor fusions.
In case 2., we get two preimage classes, there is exactly one group \(H/Z_i\) in which \(g^G\) has two preimage classes –which are in bijection with the two preimage classes of \(H\)– and for the other two groups \(H/Z_j\), the factor fusions from \(H\) map the two classes of \(H\) to the unique preimage class of \(g^G\). (In the following picture, this is shown for \(i = 1\).)
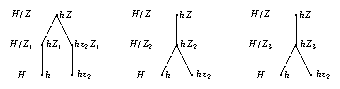
In case 3., the three factor fusions are in general not uniquely determined: We get four classes, which are defined as two pairs of preimages of the two preimages of \(g^G\) in \(H/Z_1\) and in \(H/Z_2\) –so we choose the relevant images in the two factor fusions to \(H/Z_1\) and \(H/Z_2\), respectively. Note that the class of \(h\) in \(H\) is the unique class that maps to the class of \(h Z_1\) in \(H/Z_1\) and to the class of \(h Z_2\) in \(H/Z_2\), and so on, and we define four classes of \(H\) via the four possible combinations of image classes in \(H/Z_1\) and \(H/Z_2\) (see the picture below).
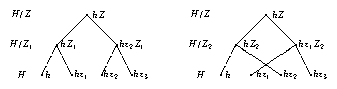
Due to the fact that in general we do not know which of the two preimage classes of \(g^G\) in \(H/Z_3\) is the class of \(h Z_3\), there are in general the following two possibilities for the fusion from \(H\) to \(H/Z_3\).
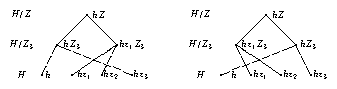
This means that we can inflate the irreducible characters of \(H/Z_1\) and of \(H/Z_2\) to \(H\) but that for the inflations of those irreducible characters of \(H/Z_3\) to \(H\) that are not characters of \(G\), the values on classes where case 3. applies are determined only up to sign.
The GAP function PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G) computes the candidates for the table of \(H\) from the tables of the groups \(H/Z_i\) by setting up the character table head of \(H\) using the class fusions from \(H/Z_1\) and \(H/Z_2\) to \(G\), and then forming the possible class fusions from \(H\) to \(H/Z_3\).
If case 3. applies for a class \(g^G\) with \(g\) of odd element order then exactly one preimage class in \(H\) has odd element order, and we can identify this class in the groups \(H/Z_i\), which resolves the ambiguity in this situation. More generally, if \(g = k^2\) holds for some \(k \in G\) then all preimages of \(k^G\) in \(H\) square to the same class of \(H\), so again this class can be identified. In fact PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G) checks whether the \(p\)-th power maps of the candidate table for \(H\) and the \(p\)-th power map of \(H/Z_3\) together with the fusion candidate form a commutative diagram.
An additional criterion used by PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G) is given by the property that the product of two characters inflated from \(H/Z_1\) and \(H/Z_2\), respectively, that are not characters of \(G\) is a character of \(H\) that contains \(Z_3\) in its kernel, so it is checked whether the scalar products of these characters with all characters that are inflated from \(H/Z_3\) via the candidate fusion are nonnegative integers.
Once the fusions from \(H\) to the groups \(H/Z_i\) are known, the computation of the irreducible \(p\)-modular characters of \(H\) from those of the groups \(H/Z_i\) is straightforward.
The only open question is why this construction is described in this note. That is, how is it related to table automorphisms?
The answer is that in several interesting cases, the three subgroups \(Z_1\), \(Z_2\), \(Z_3\) are conjugate under an order three automorphism \(\sigma\), say, of \(H\). In this situation, the three factor groups \(2_i.G = H/Z_i\) are isomorphic, and we can describe the input tables and fusions by the character table of \(2_1.G\), the factor fusion from this group to \(G\), and the automorphism \(\sigma'\) of \(G\) that is induced by \(\sigma\). Assume that \(\sigma(Z_1) = Z_2\) holds, and choose \(h \in H\). Then \(\sigma(h Z_1) = \sigma(h) Z_2\) is mapped to \(\sigma(h) Z = \sigma'(h Z)\) under the factor fusion from \(2_2.G\) to \(G\). Let us start with the character table of \(2_1.G\), and fix the class fusion to the character table of \(G\). We may choose the identity map as isomorphism from the table of \(2_1.G\) to the tables of \(2_2.G\) and \(2_3.G\), which implies that the class of \(h Z_1\) is identified with the class of \(h Z_2\) and in turn the class fusion from the table of \(2_2.G\) to that of \(G\) can be chosen as the class fusion from the table of \(2_1.G\) followed by the permutation of classes of \(G\) induced by \(\sigma'\); analogously, the fusion from the table of \(2_3.G\) is obtained by applying this permutation twice to the class fusion from the table of \(2_1.G\).
For examples, see Section 2.7.
Let \(G\) be a finite group, and \(H\) be an upward extension of \(G\) by an automorphism of prime order \(p\), say. \(H\) induces a table automorphism of the \(p\)-modular character table of \(G\); let \(\pi\) denote the corresponding permutation of classes of \(G\). The columns of the \(p\)-modular character table of \(H\) are given by the orbits of \(\pi\), and the irreducible Brauer characters of \(H\) are exactly the orbit sums of \(\pi\) on the irreducible Brauer characters of \(G\).
Note that for computing the \(p\)-modular character table of \(H\) from that of \(G\), it is sufficient to know the orbits of \(\pi\) and not \(\pi\) itself. Also the ordinary character table of \(H\) is not needed, but since GAP stores Brauer character tables relative to their ordinary tables, we are interested mainly in cases where the ordinary character tables of \(G\) and \(H\) and the \(p\)-modular character table of \(G\) are known. Assuming that the class fusion between the ordinary tables of \(G\) and \(H\) is stored on the table of \(G\), the orbits of the action of \(H\) on the \(p\)-regular classes of \(G\) can be read off from it.
The GAP function IBrOfExtensionBySingularAutomorphism (CTblLib: IBrOfExtensionBySingularAutomorphism) can be used to compute the \(p\)-modular irreducibles of \(H\).
For examples, see Section 2.8.
Let \(C_2\) denote the cyclic group of order two, let \(G_1\), \(G_2\) be two finite groups, and for \(i \in \{ 1, 2 \}\), let \(\varphi_i\colon G_i \rightarrow C_2\) be an epimorphism with kernel \(H_i\). Let \(G\) be the subdirect product (pullback) of \(G_1\) and \(G_2\) w.r.t. the epimorphisms \(\varphi_i\), i.e.,
\[ G = \{ (g_1, g_2) \in G_1 \times G_2; \varphi_1(g_1) = \varphi_2(g_2) \} . \]
The group \(G\) has index two in the direct product \(G_1 \times G_2\), and \(G\) contains \(H_1 \times H_2\) as a subgroup of index two.
In the following, we describe how the ordinary (or \(p\)-modular) character table of \(G\) can be computed from the ordinary (or \(p\)-modular) character tables of the groups \(G_i\) and \(H_i\), and the class fusions from \(H_i\) to \(G_i\).
(For the case that one of the groups \(G_i\) is a cyclic group of order four, an alternative way to construct the character table of \(G\) is described in Section 2.2-4. For the case that one of the groups \(G_i\) acts fixed point freely on the nontrivial irreducible characters of \(H_i\), an alternative construction is described in Section 2.3-1.)
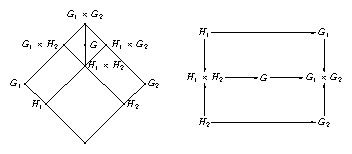
Each conjugacy class of \(G\) is either contained in \(H_1 \times H_2\) or not. In the former case, let \(h_i \in H_i\) and \(g_i \in G_i \setminus H_i\); in particular, \((g_1, g_2) \in G\) because both \(\varphi_1(g_1)\) and \(\varphi_2(g_2)\) are not the identity. There are four possibilities.
If \(h_1^{{H_1}} = h_1^{{G_1}}\) and \(h_2^{{H_2}} = h_2^{{G_2}}\) then \((h_1, h_2)^{{H_1 \times H_2}} = (h_1, h_2)^{{G_1 \times G_2}}\) holds, hence this class is equal to \((h_1, h_2)^G\).
If \(h_1^{{H_1}} ≠ h_1^{{G_1}}\) and \(h_2^{{H_2}} ≠ h_2^{{G_2}}\) then the four \(H_1 \times H_2\)-classes with the representatives \((h_1, h_2)\), \((h_1^{{g_1}}, h_2)\), \((h_1, h_2^{{g_2}})\), and \((h_1^{{g_1}}, h_2^{{g_2}})\) fall into two \(G\)-classes, where \((h_1, h_2)\) is \(G\)-conjugate with \((h_1^{{g_1}}, h_2^{{g_2}})\), and \((h_1^{{g_1}}, h_2)\) is \(G\)-conjugate with \((h_1, h_2^{{g_2}})\).
If \(h_1^{{H_1}} = h_1^{{G_1}}\) and \(h_2^{{H_2}} ≠ h_2^{{G_2}}\) then the two \(H_1 \times H_2\)-classes with the representatives \((h_1, h_2)\) and \((h_1, h_2^{{g_2}})\) fuse in \(G\); note that there is \(\tilde{g}_1 \in C_{{G_1}}(h_1) \setminus H_1\), so \((\tilde{g}_1, g_2) \in G\) holds.
The case of \(h_1^{{H_1}} ≠ h_1^{{G_1}}\) and \(h_2^{{H_2}} = h_2^{{G_2}}\) is analogous to case 3.
It remains to deal with the \(G\)-classes that are not contained in \(H_1 \times H_2\). Each such class is in fact a conjugacy class of \(G_1 \times G_2\). Note that two elements \(g_1, g_2 \in G_1 \setminus H_1\) are \(G_1\)-conjugate if and only if they are \(H_1\)-conjugate. (If \(g_1^x = g_2\) for \(x \in G_1 \setminus H_1\) then \(g_1^{{g_1 x}} = g_2\) holds, and \(g_1 x \in H_1\).) This implies \((g_1, g_2)^{{G_1 \times G_2}} = (g_1, g_2)^{{H_1 \times H_2}}\), and thus this class is equal to \((g_1, g_2)^G\).
The (ordinary or \(p\)-modular) irreducible characters of \(G\) are given by the restrictions \(\chi_G\) of all those irreducible characters \(\chi\) of \(G_1 \times G_2\) whose restriction to \(H_1 \times H_2\) is irreducible, plus the induced characters \(\varphi^G\), where \(\varphi\) runs over all those irreducible characters of \(H_1 \times H_2\) that do not occur as restrictions of characters of \(G_1 \times G_2\).
In other words, no irreducible character of \(H_1 \times H_2\) has inertia subgroup \(G\) inside \(G_1 \times G_2\). This can be seen as follows. Let \(\varphi\) be an irreducible character of \(H_1 \times H_2\). Then \(\varphi = \varphi_1 \cdot \varphi_2\), where \(\varphi_1\), \(\varphi_2\) are irreducible characters of \(H_1 \times H_2\) with the properties that \(H_2 \subseteq \ker(\varphi_1)\) and \(H_1 \subseteq \ker(\varphi_2)\). Sloppy speaking, \(\varphi_i\) is an irreducible character of \(H_i\).
There are four possibilities.
If \(\varphi_1\) extends to \(G_1\) and \(\varphi_2\) extends to \(G_2\) then \(\varphi\) extends to \(G\), so \(\varphi\) has inertia subgroup \(G_1 \times G_2\).
If \(\varphi_1\) does not extend to \(G_1\) and \(\varphi_2\) does not extend to \(G_2\) then \(\varphi^{{G_1 \times G_2}}\) is irreducible, so \(\varphi\) has inertia subgroup \(H_1 \times H_2\).
If \(\varphi_1\) extends to \(G_1\) and \(\varphi_2\) does not extend to \(G_2\) then \(\varphi\) extends to \(G_1 \times H_2\) but not to \(G_1 \times G_2\), so \(\varphi\) has inertia subgroup \(G_1 \times H_2\).
The case that \(\varphi_1\) does not extend to \(G_1\) and \(\varphi_2\) extends to \(G_2\) is analogous to case 3, \(\varphi\) has inertia subgroup \(H_1 \times G_2\).
For examples, see Section 2.9.
Let \(n = 2^k \cdot m\) where \(k\) is a nonnegative integer and \(m\) is an odd integer, and consider the dihedral group \(D_{2n}\) of order \(2n\). Let \(N\) denote the derived subgroup of \(D_{2n}\).
If \(k = 0\) then \(D_{2n}\) has the structure \(M.G.A\), with \(M = N\) and \(G\) the trivial group, and \(A\) a cyclic group of order two that inverts each element of \(N\) and hence acts fixed-point freely on \(N\). The smallest nontrivial example is of course that of \(D_6 \cong S_3\).
gap> tblMG:= CharacterTable( "Cyclic", 3 );; gap> tblG:= CharacterTable( "Cyclic", 1 );; gap> tblGA:= CharacterTable( "Cyclic", 2 );; gap> StoreFusion( tblMG, [ 1, 1, 1 ], tblG ); gap> StoreFusion( tblG, [ 1 ], tblGA ); gap> elms:= Elements( AutomorphismsOfTable( tblMG ) ); [ (), (2,3) ] gap> orbs:= [ [ 1 ], [ 2, 3 ] ];; gap> new:= PossibleCharacterTablesOfTypeMGA( tblMG, tblG, tblGA, orbs, > "S3" ); [ rec( MGfusMGA := [ 1, 2, 2 ], table := CharacterTable( "S3" ) ) ] gap> Display( new[1].table ); S3 2 1 . 1 3 1 1 . 1a 3a 2a 2P 1a 3a 1a 3P 1a 1a 2a X.1 1 1 1 X.2 1 1 -1 X.3 2 -1 .
If \(k > 0\) then \(D_{2n}\) has the structure \(M.G.A\), with \(M = N\) and \(G\) a cyclic group of order two such that \(M.G\) is cyclic, and \(A\) is a cyclic group of order two that inverts each element of \(M.G\) and hence acts fixed-point freely on \(M.G\). The smallest nontrivial example is of course that of \(D_8\).
gap> tblMG:= CharacterTable( "Cyclic", 4 );; gap> tblG:= CharacterTable( "Cyclic", 2 );; gap> tblGA:= CharacterTable( "2^2" );; gap> OrdersClassRepresentatives( tblMG ); [ 1, 4, 2, 4 ] gap> StoreFusion( tblMG, [ 1, 2, 1, 2 ], tblG ); gap> StoreFusion( tblG, [ 1, 2 ], tblGA ); gap> elms:= Elements( AutomorphismsOfTable( tblMG ) ); [ (), (2,4) ] gap> orbs:= Orbits( Group( elms[2] ), [ 1 ..4 ] );; gap> new:= PossibleCharacterTablesOfTypeMGA( tblMG, tblG, tblGA, orbs, > "order8" ); [ rec( MGfusMGA := [ 1, 2, 3, 2 ], table := CharacterTable( "order8" ) ), rec( MGfusMGA := [ 1, 2, 3, 2 ], table := CharacterTable( "order8" ) ) ]
Here we get two possible tables, which are the character tables of the dihedral and the quaternion group of order eight, respectively.
gap> List( new, x -> OrdersClassRepresentatives( x.table ) ); [ [ 1, 4, 2, 2, 2 ], [ 1, 4, 2, 4, 4 ] ] gap> Display( new[1].table ); order8 2 3 2 3 2 2 1a 4a 2a 2b 2c 2P 1a 2a 1a 1a 1a X.1 1 1 1 1 1 X.2 1 1 1 -1 -1 X.3 1 -1 1 1 -1 X.4 1 -1 1 -1 1 X.5 2 . -2 . .
For each \(k > 1\) and \(m = 1\), we get two possible tables this way, that of the dihedral group of order \(2^{k+1}\) and that of the generalized quaternion group of order \(2^{k+1}\).
The Sylow \(7\) normalizer in the symmetric group \(S_{12}\) has the structure \(7:6 \times S_5\), its intersection \(N\) with the alternating group \(A_{12}\) is of index two, it has the structure \((7:3 \times A_5):2\).
Let \(M\) denote the normal subgroup of order \(7\) in \(N\), let \(G\) denote the normal subgroup of the type \(3 \times A_5\) in \(F = N/M \cong 3 \times S_5\), and \(A = F/G\), the cyclic group of order two. Then \(N\) has the structure \(M.G.A\), where \(A\) acts fixed-point freely on the irreducible characters of \(M.G = 7:3 \times A_5\) that do not contain \(M\) in their kernels, hence the character table of \(N\) is determined by the character tables of \(M.G\) and \(F\), and the action of \(A\) on \(M.G\).
Note that in this example, the group \(M\) is not central in \(M.G\), unlike in most of our examples.
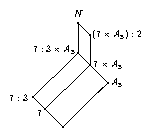
gap> tblMG:= CharacterTable( "7:3" ) * CharacterTable( "A5" );; gap> nsg:= ClassPositionsOfNormalSubgroups( tblMG ); [ [ 1 ], [ 1, 6 .. 11 ], [ 1 .. 5 ], [ 1, 6 .. 21 ], [ 1 .. 15 ], [ 1 .. 25 ] ] gap> List( nsg, x -> Sum( SizesConjugacyClasses( tblMG ){ x } ) ); [ 1, 7, 60, 21, 420, 1260 ] gap> tblG:= tblMG / nsg[2];; gap> tblGA:= CharacterTable( "Cyclic", 3 ) * CharacterTable( "A5.2" );; gap> GfusGA:= PossibleClassFusions( tblG, tblGA ); [ [ 1, 2, 3, 4, 4, 8, 9, 10, 11, 11, 15, 16, 17, 18, 18 ], [ 1, 2, 3, 4, 4, 15, 16, 17, 18, 18, 8, 9, 10, 11, 11 ] ] gap> reps:= RepresentativesFusions( Group(()), GfusGA, tblGA ); [ [ 1, 2, 3, 4, 4, 8, 9, 10, 11, 11, 15, 16, 17, 18, 18 ] ] gap> StoreFusion( tblG, reps[1], tblGA ); gap> acts:= PossibleActionsForTypeMGA( tblMG, tblG, tblGA ); [ [ [ 1 ], [ 2 ], [ 3 ], [ 4, 5 ], [ 6, 11 ], [ 7, 12 ], [ 8, 13 ], [ 9, 15 ], [ 10, 14 ], [ 16 ], [ 17 ], [ 18 ], [ 19, 20 ], [ 21 ], [ 22 ], [ 23 ], [ 24, 25 ] ] ] gap> poss:= PossibleCharacterTablesOfTypeMGA( tblMG, tblG, tblGA, > acts[1], "A12N7" ); [ rec( MGfusMGA := [ 1, 2, 3, 4, 4, 5, 6, 7, 8, 9, 5, 6, 7, 9, 8, 10, 11, 12, 13, 13, 14, 15, 16, 17, 17 ], table := CharacterTable( "A12N7" ) ) ]
Let us compare the result table with the table of the Sylow \(7\) normalizer in \(A_{12}\).
gap> g:= AlternatingGroup( 12 );; gap> IsRecord( TransformingPermutationsCharacterTables( poss[1].table, > CharacterTable( Normalizer( g, SylowSubgroup( g, 7 ) ) ) ) ); true
Since July 2007, an alternative way to construct the character table of \(N\) from other character tables is to exploit its structure as a subdirect product of index two in the group \(7:6 \times S_5\), see Section 2.3-6.
gap> tblh1:= CharacterTable( "7:3" );; gap> tblg1:= CharacterTable( "7:6" );; gap> tblh2:= CharacterTable( "A5" );; gap> tblg2:= CharacterTable( "A5.2" );; gap> subdir:= CharacterTableOfIndexTwoSubdirectProduct( tblh1, tblg1, > tblh2, tblg2, "(7:3xA5).2" );; gap> IsRecord( TransformingPermutationsCharacterTables( poss[1].table, > subdir.table ) ); true
For storing the table of \(N\) in the GAP Character Table Library, the construction as a subdirect product is more suitable, since the auxiliary table
of the direct product \(7:3 \times A_5\) need not be stored in the library.
We show the construction of some character tables of groups of the type \(M.G.A\) that are contained in the GAP Character Table Library. Each entry in the following input list contains the names of the library character tables of \(M.G\), \(G\), \(G.A\), and \(M.G.A\).
First we consider the situation where \(G\) is a simple group or a central extension of a simple group whose character table is shown in the Atlas, and \(M\) and \(A\) are cyclic groups such that \(M\) is central in \(M.G\).
In the following cases, the character tables are uniquely determined by the input tables. Note that in each of these cases, \(|A|\) and \(|M|\) are coprime.
gap> listMGA:= [ > [ "3.A6", "A6", "A6.2_1", "3.A6.2_1" ], > [ "3.A6", "A6", "A6.2_2", "3.A6.2_2" ], > [ "6.A6", "2.A6", "2.A6.2_1", "6.A6.2_1" ], > [ "6.A6", "2.A6", "2.A6.2_2", "6.A6.2_2" ], > [ "3.A7", "A7", "A7.2", "3.A7.2" ], > [ "6.A7", "2.A7", "2.A7.2", "6.A7.2" ], > [ "3.L3(4)", "L3(4)", "L3(4).2_2", "3.L3(4).2_2" ], > [ "3.L3(4)", "L3(4)", "L3(4).2_3", "3.L3(4).2_3" ], > [ "6.L3(4)", "2.L3(4)", "2.L3(4).2_2", "6.L3(4).2_2" ], > [ "6.L3(4)", "2.L3(4)", "2.L3(4).2_3", "6.L3(4).2_3" ], > [ "12_1.L3(4)", "4_1.L3(4)", "4_1.L3(4).2_2", "12_1.L3(4).2_2" ], > [ "12_1.L3(4)", "4_1.L3(4)", "4_1.L3(4).2_3", "12_1.L3(4).2_3" ], > [ "12_2.L3(4)", "4_2.L3(4)", "4_2.L3(4).2_2", "12_2.L3(4).2_2" ], > [ "12_2.L3(4)", "4_2.L3(4)", "4_2.L3(4).2_3", "12_2.L3(4).2_3" ], > [ "3.U3(5)", "U3(5)", "U3(5).2", "3.U3(5).2" ], > [ "3.M22", "M22", "M22.2", "3.M22.2" ], > [ "6.M22", "2.M22", "2.M22.2", "6.M22.2" ], > [ "12.M22", "4.M22", "4.M22.2", "12.M22.2" ], > [ "3.L3(7)", "L3(7)", "L3(7).2", "3.L3(7).2" ], > [ "3_1.U4(3)", "U4(3)", "U4(3).2_1", "3_1.U4(3).2_1" ], > [ "3_1.U4(3)", "U4(3)", "U4(3).2_2'", "3_1.U4(3).2_2'" ], > [ "3_2.U4(3)", "U4(3)", "U4(3).2_1", "3_2.U4(3).2_1" ], > [ "3_2.U4(3)", "U4(3)", "U4(3).2_3'", "3_2.U4(3).2_3'" ], > [ "6_1.U4(3)", "2.U4(3)", "2.U4(3).2_1", "6_1.U4(3).2_1" ], > [ "6_1.U4(3)", "2.U4(3)", "2.U4(3).2_2'", "6_1.U4(3).2_2'" ], > [ "6_2.U4(3)", "2.U4(3)", "2.U4(3).2_1", "6_2.U4(3).2_1" ], > [ "6_2.U4(3)", "2.U4(3)", "2.U4(3).2_3'", "6_2.U4(3).2_3'" ], > [ "12_1.U4(3)", "4.U4(3)", "4.U4(3).2_1", "12_1.U4(3).2_1" ], > [ "12_2.U4(3)", "4.U4(3)", "4.U4(3).2_1", "12_2.U4(3).2_1" ], > [ "3.G2(3)", "G2(3)", "G2(3).2", "3.G2(3).2" ], > [ "3.U3(8)", "U3(8)", "U3(8).2", "3.U3(8).2" ], > [ "3.U3(8).3_1", "U3(8).3_1", "U3(8).6", "3.U3(8).6" ], > [ "3.J3", "J3", "J3.2", "3.J3.2" ], > [ "3.U3(11)", "U3(11)", "U3(11).2", "3.U3(11).2" ], > [ "3.McL", "McL", "McL.2", "3.McL.2" ], > [ "3.O7(3)", "O7(3)", "O7(3).2", "3.O7(3).2" ], > [ "6.O7(3)", "2.O7(3)", "2.O7(3).2", "6.O7(3).2" ], > [ "3.U6(2)", "U6(2)", "U6(2).2", "3.U6(2).2" ], > [ "6.U6(2)", "2.U6(2)", "2.U6(2).2", "6.U6(2).2" ], > [ "3.Suz", "Suz", "Suz.2", "3.Suz.2" ], > [ "6.Suz", "2.Suz", "2.Suz.2", "6.Suz.2" ], > [ "3.ON", "ON", "ON.2", "3.ON.2" ], > [ "3.Fi22", "Fi22", "Fi22.2", "3.Fi22.2" ], > [ "6.Fi22", "2.Fi22", "2.Fi22.2", "6.Fi22.2" ], > [ "3.2E6(2)", "2E6(2)", "2E6(2).2", "3.2E6(2).2" ], > [ "6.2E6(2)", "2.2E6(2)", "2.2E6(2).2", "6.2E6(2).2" ], > [ "3.F3+", "F3+", "F3+.2", "3.F3+.2" ], > ];;
(We need not consider groups \(3.U_3(8).6'\) and \(3.U_3(8).6'\), see Section 2.4-7.)
Note that the groups of the types \(12_1.L_3(4).2_1\) and \(12_2.L_3(4).2_1\) have central subgroups of order six, so we cannot choose \(G\) equal to \(4_1.L_3(4)\) and \(4_2.L_3(4)\), respectively, in these cases. See Section 2.4-4 for the construction of these tables.
Also in the following cases, \(|A|\) and \(|M|\) are coprime, we have \(|M| = 3\) and \(|A| = 2\). The group \(M.G\) has a central subgroup of the type \(2^2 \times 3\), and \(A\) acts on this group by inverting the elements in the subgroup of order \(3\) and by swapping two involutions in the Klein four group.
gap> Append( listMGA, [ > [ "(2^2x3).L3(4)", "2^2.L3(4)", "2^2.L3(4).2_2", "(2^2x3).L3(4).2_2" ], > [ "(2^2x3).L3(4)", "2^2.L3(4)", "2^2.L3(4).2_3", "(2^2x3).L3(4).2_3" ], > [ "(2^2x3).U6(2)", "2^2.U6(2)", "2^2.U6(2).2", "(2^2x3).U6(2).2" ], > [ "(2^2x3).2E6(2)", "2^2.2E6(2)", "2^2.2E6(2).2", "(2^2x3).2E6(2).2" ], > ] );
Additionally, there are a few cases where \(A\) has order two, and \(G.A\) has a factor group of the type \(2^2\), and a few cases where \(M\) has the type \(2^2\) and \(A\) is of order three and acts transitively on the involutions in \(M\).
gap> Append( listMGA, [ > [ "3.A6.2_3", "A6.2_3", "A6.2^2", "3.A6.2^2" ], > [ "3.L3(4).2_1", "L3(4).2_1", "L3(4).2^2", "3.L3(4).2^2" ], > [ "3_1.U4(3).2_2", "U4(3).2_2", "U4(3).(2^2)_{122}", > "3_1.U4(3).(2^2)_{122}" ], > [ "3_2.U4(3).2_3", "U4(3).2_3", "U4(3).(2^2)_{133}", > "3_2.U4(3).(2^2)_{133}" ], > [ "3^2.U4(3).2_3'", "3_2.U4(3).2_3'", "3_2.U4(3).(2^2)_{133}", > "3^2.U4(3).(2^2)_{133}" ], > [ "2^2.L3(4)", "L3(4)", "L3(4).3", "2^2.L3(4).3" ], > [ "(2^2x3).L3(4)", "3.L3(4)", "3.L3(4).3", "(2^2x3).L3(4).3" ], > [ "2^2.L3(4).2_1", "L3(4).2_1", "L3(4).6", "2^2.L3(4).6" ], > [ "2^2.Sz(8)", "Sz(8)", "Sz(8).3", "2^2.Sz(8).3" ], > [ "2^2.U6(2)", "U6(2)", "U6(2).3", "2^2.U6(2).3" ], > [ "(2^2x3).U6(2)", "3.U6(2)", "3.U6(2).3", "(2^2x3).U6(2).3" ], > [ "2^2.O8+(2)", "O8+(2)", "O8+(2).3", "2^2.O8+(2).3" ], > [ "2^2.O8+(3)", "O8+(3)", "O8+(3).3", "2^2.O8+(3).3" ], > [ "2^2.2E6(2)", "2E6(2)", "2E6(2).3", "2^2.2E6(2).3" ], > ] );
The constructions of the character tables of groups of the types \(4_2.L_3(4).2_3\), \(12_2.L_3(4).2_3\), \(12_1.U_4(3).2_2'\) and \(12_2.U_4(3).2_3'\) is described in Section 2.4-5 and 2.4-6, in these cases the GAP functions return several possible tables.
The construction of the various character table of groups of the types \(4_1.L_3(4).2^2\) and \(4_2.L_3(4).2^2\) are described in Section 2.6-7.
The following function takes the ordinary character tables of the groups \(M.G\), \(G\), and \(G.A\), a string to be used as the Identifier (Reference: Identifier for tables of marks) value of the character table of \(M.G.A\), and the character table of \(M.G.A\) that is contained in the GAP Character Table Library; the function first computes the possible actions of \(G.A\) on the classes of \(M.G\), using the function PossibleActionsForTypeMGA (CTblLib: PossibleActionsForTypeMGA), then computes the union of possible character tables for these actions, and then representatives up to permutation equivalence; if there is only one solution then the result table is compared with the library table.
gap> ConstructOrdinaryMGATable:= function( tblMG, tblG, tblGA, name, lib ) > local acts, poss, trans; > > acts:= PossibleActionsForTypeMGA( tblMG, tblG, tblGA ); > poss:= Concatenation( List( acts, pi -> > PossibleCharacterTablesOfTypeMGA( tblMG, tblG, tblGA, pi, > name ) ) ); > poss:= RepresentativesCharacterTables( poss ); > if Length( poss ) = 1 then > # Compare the computed table with the library table. > if not IsCharacterTable( lib ) then > List( poss, x -> AutomorphismsOfTable( x.table ) ); > Print( "#I no library table for ", name, "\n" ); > else > trans:= TransformingPermutationsCharacterTables( poss[1].table, > lib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " differ\n" ); > fi; > # Compare the computed fusion with the stored one. > if OnTuples( poss[1].MGfusMGA, trans.columns ) > <> GetFusionMap( tblMG, lib ) then > Print( "#E computed and stored fusion for ", name, > " differ\n" ); > fi; > fi; > elif Length( poss ) = 0 then > Print( "#E no solution for ", name, "\n" ); > else > Print( "#E ", Length( poss ), " possibilities for ", name, "\n" ); > fi; > return poss; > end;;
The following function takes the ordinary character tables of the groups \(M.G\), \(G.A\), and \(M.G.A\), and tries to construct the \(p\)-modular character tables of \(M.G.A\) from the \(p\)-modular character tables of the first two of these tables, for all prime divisors \(p\) of the order of \(M.G.A\). Note that the tables of \(G\) are not needed in the construction, only the class fusions from \(M.G\) to \(M.G.A\) and from \(M.G.A\) to \(G.A\) must be stored.
gap> ConstructModularMGATables:= function( tblMG, tblGA, ordtblMGA ) > local name, poss, p, modtblMG, modtblGA, modtblMGA, modlib, trans; > > name:= Identifier( ordtblMGA ); > poss:= []; > for p in PrimeDivisors( Size( ordtblMGA ) ) do > modtblMG := tblMG mod p; > modtblGA := tblGA mod p; > if ForAll( [ modtblMG, modtblGA ], IsCharacterTable ) then > modtblMGA:= BrauerTableOfTypeMGA( modtblMG, modtblGA, ordtblMGA ); > Add( poss, modtblMGA ); > modlib:= ordtblMGA mod p; > if IsCharacterTable( modlib ) then > trans:= TransformingPermutationsCharacterTables( modtblMGA.table, > modlib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " mod ", p, " differ\n" ); > fi; > else > AutomorphismsOfTable( modtblMGA.table ); > Print( "#I no library table for ", name, " mod ", p, "\n" ); > fi; > else > Print( "#I not all input tables for ", name, " mod ", p, > " available\n" ); > fi; > od; > > return poss; > end;;
Now we run the constructions for the cases in the list. Note that in order to avoid conflicts of the class fusions that arise in the construction with the class fusions that are already stored on the library tables, we choose identifiers for the result tables that are different from the identifiers of the library tables.
gap> for input in listMGA do > tblMG := CharacterTable( input[1] ); > tblG := CharacterTable( input[2] ); > tblGA := CharacterTable( input[3] ); > name := Concatenation( "new", input[4] ); > lib := CharacterTable( input[4] ); > poss:= ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib ); > if 1 <> Length( poss ) then > Print( "#I ", Length( poss ), " possibilities for ", name, "\n" ); > elif lib = fail then > Print( "#I no library table for ", input[4], "\n" ); > else > ConstructModularMGATables( tblMG, tblGA, lib ); > fi; > od; #I not all input tables for 3.2E6(2).2 mod 2 available #I not all input tables for 3.2E6(2).2 mod 3 available #I not all input tables for 3.2E6(2).2 mod 5 available #I not all input tables for 3.2E6(2).2 mod 7 available #I not all input tables for 3.2E6(2).2 mod 11 available #I not all input tables for 3.2E6(2).2 mod 13 available #I not all input tables for 3.2E6(2).2 mod 17 available #I not all input tables for 3.2E6(2).2 mod 19 available #I not all input tables for 6.2E6(2).2 mod 2 available #I not all input tables for 6.2E6(2).2 mod 3 available #I not all input tables for 6.2E6(2).2 mod 5 available #I not all input tables for 6.2E6(2).2 mod 7 available #I not all input tables for 6.2E6(2).2 mod 11 available #I not all input tables for 6.2E6(2).2 mod 13 available #I not all input tables for 6.2E6(2).2 mod 17 available #I not all input tables for 6.2E6(2).2 mod 19 available #I not all input tables for 3.F3+.2 mod 2 available #I not all input tables for 3.F3+.2 mod 3 available #I not all input tables for 3.F3+.2 mod 5 available #I not all input tables for 3.F3+.2 mod 7 available #I not all input tables for 3.F3+.2 mod 13 available #I not all input tables for 3.F3+.2 mod 17 available #I not all input tables for 3.F3+.2 mod 29 available #I not all input tables for (2^2x3).2E6(2).2 mod 2 available #I not all input tables for (2^2x3).2E6(2).2 mod 3 available #I not all input tables for (2^2x3).2E6(2).2 mod 5 available #I not all input tables for (2^2x3).2E6(2).2 mod 7 available #I not all input tables for (2^2x3).2E6(2).2 mod 11 available #I not all input tables for (2^2x3).2E6(2).2 mod 13 available #I not all input tables for (2^2x3).2E6(2).2 mod 17 available #I not all input tables for (2^2x3).2E6(2).2 mod 19 available #I not all input tables for 3^2.U4(3).(2^2)_{133} mod 2 available #I not all input tables for 3^2.U4(3).(2^2)_{133} mod 5 available #I not all input tables for 3^2.U4(3).(2^2)_{133} mod 7 available #I not all input tables for 2^2.O8+(3).3 mod 5 available #I not all input tables for 2^2.O8+(3).3 mod 7 available #I not all input tables for 2^2.O8+(3).3 mod 13 available #I not all input tables for 2^2.2E6(2).3 mod 2 available #I not all input tables for 2^2.2E6(2).3 mod 3 available #I not all input tables for 2^2.2E6(2).3 mod 5 available #I not all input tables for 2^2.2E6(2).3 mod 7 available #I not all input tables for 2^2.2E6(2).3 mod 11 available #I not all input tables for 2^2.2E6(2).3 mod 13 available #I not all input tables for 2^2.2E6(2).3 mod 17 available #I not all input tables for 2^2.2E6(2).3 mod 19 available
We do not get any unexpected output, so the character tables in question are determined by the inputs.
Alternative constructions of the character tables of \(3.A_6.2^2\), \(3.L_3(4).2^2\), and \(3_2.U_4(3).(2^2)_{133}\) can be found in Section 2.6-2.
In the following situations, we have \(|A| = 2\), and \(|M|\) is a multiple of \(2\). The result turns out to be unique up to isoclinism, see Section 2.3-1.
First, there are some cases where the centre of \(M.G\) is a cyclic group of order four, and \(|M| = 2\) holds.
gap> listMGA2:= [ > [ "4_1.L3(4)", "2.L3(4)", "2.L3(4).2_1", "4_1.L3(4).2_1" ], > [ "4_1.L3(4)", "2.L3(4)", "2.L3(4).2_2", "4_1.L3(4).2_2" ], > [ "4_2.L3(4)", "2.L3(4)", "2.L3(4).2_1", "4_2.L3(4).2_1" ], > [ "4.M22", "2.M22", "2.M22.2", "4.M22.2" ], > [ "4.U4(3)", "2.U4(3)", "2.U4(3).2_2", "4.U4(3).2_2" ], > [ "4.U4(3)", "2.U4(3)", "2.U4(3).2_3", "4.U4(3).2_3" ], > ];;
Note that the groups \(4_1.L3(4).2_3\) and \(4_2.L3(4).2_2\) and their isoclinic variants have centres of order four, so they do not appear here. The construction of the character table of \(4_2.L_3(4).2_3\) is more involved, it is described in Section 2.4-5.
Also in the following cases, we have \(|M| = 2\), but the situation is different because \(M.G\) has a central subgroup of the type \(2^2\) containing a unique subgroup of order \(2\) that is central in \(M.G.A\).
gap> Append( listMGA2, [ > [ "2^2.L3(4)", "2.L3(4)", "2.L3(4).2_2", "2^2.L3(4).2_2" ], > [ "2^2.L3(4)", "2.L3(4)", "2.L3(4).2_3", "2^2.L3(4).2_3" ], > [ "2^2.L3(4).2_1", "2.L3(4).2_1", "2.L3(4).(2^2)_{123}", "2^2.L3(4).2^2" ], > [ "2^2.O8+(2)", "2.O8+(2)", "2.O8+(2).2", "2^2.O8+(2).2" ], > [ "2^2.U6(2)", "2.U6(2)", "2.U6(2).2", "2^2.U6(2).2" ], > [ "2^2.2E6(2)", "2.2E6(2)", "2.2E6(2).2", "2^2.2E6(2).2" ], > ] );
Next there are two constructions for \(G = 6.L_3(4)\), with \(|M| = 12\) and \(|A| = 2\). Note that the groups \(12_1.L3(4).2_1\) and \(12_2.L3(4).2_1\) have central subgroups of the order six, so we cannot use the factor groups \(4_1.L3(4).2_1\) and \(4_2.L3(4).2_1\), respectively, for the constructions.
gap> Append( listMGA2, [ > [ "12_1.L3(4)", "6.L3(4)", "6.L3(4).2_1", "12_1.L3(4).2_1" ], > [ "12_2.L3(4)", "6.L3(4)", "6.L3(4).2_1", "12_2.L3(4).2_1" ], > ] );
Next there are alternative constructions for tables which have been constructed in Section 2.4-3. There we had viewed the groups of the structure \(12.S.2\), for a simple group \(S\), as \(3.G.2\) with \(G = 4.S\). Here we view these groups as \(2.G.2\) with \(G = 6.S\), which means that we do not prescribe the \(4.S.2\) type factor group. So it is not surprising that we get more than one solution, and that the computation of the \(2\)-power map of \(12.S.2\) is more involved. Note that the construction of the character table of \(12_2.L_3(4).2_3\) is more involved, it is described in Section 2.4-5.
gap> Append( listMGA2, [ > [ "12.M22", "6.M22", "6.M22.2", "12.M22.2" ], > [ "12_1.L3(4)", "6.L3(4)", "6.L3(4).2_2", "12_1.L3(4).2_2" ], > [ "12_1.U4(3)", "6_1.U4(3)", "6_1.U4(3).2_2", "12_1.U4(3).2_2" ], > [ "12_2.U4(3)", "6_2.U4(3)", "6_2.U4(3).2_3", "12_2.U4(3).2_3" ], > ] );
Finally, there are alternative constructions for the cases where the group \(M.G\) has a central subgroup of the type \(2^2 \times 3\), and \(A\) acts on this group by inverting the elements in the subgroup of order \(3\) and by swapping two involutions in the Klein four group.
gap> Append( listMGA2, [ > [ "(2^2x3).L3(4)", "6.L3(4)", "6.L3(4).2_2", "(2^2x3).L3(4).2_2" ], > [ "(2^2x3).L3(4)", "6.L3(4)", "6.L3(4).2_3", "(2^2x3).L3(4).2_3" ], > [ "(2^2x3).U6(2)", "6.U6(2)", "6.U6(2).2", "(2^2x3).U6(2).2" ], > [ "(2^2x3).2E6(2)", "6.2E6(2)", "6.2E6(2).2", "(2^2x3).2E6(2).2" ], > ] );
Now we run the constructions for the cases in the list.
gap> for input in listMGA2 do > tblMG := CharacterTable( input[1] ); > tblG := CharacterTable( input[2] ); > tblGA := CharacterTable( input[3] ); > name := Concatenation( "new", input[4] ); > lib := CharacterTable( input[4] ); > poss:= ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib ); > if Length( poss ) = 2 then > iso:= CharacterTableIsoclinic( poss[1].table ); > if IsRecord( TransformingPermutationsCharacterTables( poss[2].table, > iso ) ) then > Unbind( poss[2] ); > fi; > elif Length( poss ) = 1 then > Print( "#I unique up to permutation equivalence: ", name, "\n" ); > fi; > if 1 <> Length( poss ) then > Print( "#I ", Length( poss ), " possibilities for ", name, "\n" ); > elif lib = fail then > Print( "#I no library table for ", input[4], "\n" ); > else > ConstructModularMGATables( tblMG, tblGA, lib ); > fi; > od; #E 2 possibilities for new4_1.L3(4).2_1 #E 2 possibilities for new4_1.L3(4).2_2 #E 2 possibilities for new4_2.L3(4).2_1 #E 2 possibilities for new4.M22.2 #E 2 possibilities for new4.U4(3).2_2 #E 2 possibilities for new4.U4(3).2_3 #I unique up to permutation equivalence: new2^2.L3(4).2_2 #I unique up to permutation equivalence: new2^2.L3(4).2_3 #I unique up to permutation equivalence: new2^2.L3(4).2^2 #I unique up to permutation equivalence: new2^2.O8+(2).2 #I unique up to permutation equivalence: new2^2.U6(2).2 #I unique up to permutation equivalence: new2^2.2E6(2).2 #I not all input tables for 2^2.2E6(2).2 mod 2 available #I not all input tables for 2^2.2E6(2).2 mod 3 available #I not all input tables for 2^2.2E6(2).2 mod 5 available #I not all input tables for 2^2.2E6(2).2 mod 7 available #E 2 possibilities for new12_1.L3(4).2_1 #E 2 possibilities for new12_2.L3(4).2_1 #E 2 possibilities for new12.M22.2 #E 2 possibilities for new12_1.L3(4).2_2 #E 2 possibilities for new12_1.U4(3).2_2 #E 2 possibilities for new12_2.U4(3).2_3 #I unique up to permutation equivalence: new(2^2x3).L3(4).2_2 #I unique up to permutation equivalence: new(2^2x3).L3(4).2_3 #I unique up to permutation equivalence: new(2^2x3).U6(2).2 #I unique up to permutation equivalence: new(2^2x3).2E6(2).2 #I not all input tables for (2^2x3).2E6(2).2 mod 2 available #I not all input tables for (2^2x3).2E6(2).2 mod 3 available #I not all input tables for (2^2x3).2E6(2).2 mod 5 available #I not all input tables for (2^2x3).2E6(2).2 mod 7 available #I not all input tables for (2^2x3).2E6(2).2 mod 11 available #I not all input tables for (2^2x3).2E6(2).2 mod 13 available #I not all input tables for (2^2x3).2E6(2).2 mod 17 available #I not all input tables for (2^2x3).2E6(2).2 mod 19 available
Again, we do not get any unexpected output, so the character tables in question are determined up to isoclinism by the inputs.
In the construction of the character table of \(M.G.A = 4_2.L_3(4).2_3\) from the tables of \(M.G = 4_2.L_3(4)\) and \(G.A = 2.L_3(4).2_3\), the action of \(A\) on the classes of \(M.G\) is uniquely determined, but we get four possible character tables.
gap> tblMG := CharacterTable( "4_2.L3(4)" );; gap> tblG := CharacterTable( "2.L3(4)" );; gap> tblGA := CharacterTable( "2.L3(4).2_3" );; gap> name := "new4_2.L3(4).2_3";; gap> lib := CharacterTable( "4_2.L3(4).2_3" );; gap> poss := ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib ); #E 4 possibilities for new4_2.L3(4).2_3 [ rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 7, 9, 10, 11, 10, 12, 12, 13, 14, 15, 14, 16, 17, 18, 17, 19, 20, 21, 22, 19, 22, 21, 20 ], table := CharacterTable( "new4_2.L3(4).2_3" ) ), rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 7, 9, 10, 11, 10, 12, 12, 13, 14, 15, 14, 16, 17, 18, 17, 19, 20, 21, 22, 19, 22, 21, 20 ], table := CharacterTable( "new4_2.L3(4).2_3" ) ), rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 7, 9, 10, 11, 10, 12, 12, 13, 14, 15, 14, 16, 17, 18, 17, 19, 20, 21, 22, 19, 22, 21, 20 ], table := CharacterTable( "new4_2.L3(4).2_3" ) ), rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 7, 9, 10, 11, 10, 12, 12, 13, 14, 15, 14, 16, 17, 18, 17, 19, 20, 21, 22, 19, 22, 21, 20 ], table := CharacterTable( "new4_2.L3(4).2_3" ) ) ]
The centre of \(4_2.L_3(4)\) is inverted by the action of the outer automorphism, so the existence of two possible tables can be expected because two isoclinic groups of the type \(4_2.L_3(4).2_3\) exist, see Section 2.2-6.
Indeed the result consists of two pairs of isoclinic tables, so we have to decide which pair of tables belongs to the groups of the type \(4_2.L_3(4).2_3\).
gap> IsRecord( TransformingPermutationsCharacterTables( poss[1].table, > CharacterTableIsoclinic( poss[4].table ) ) ); true gap> IsRecord( TransformingPermutationsCharacterTables( poss[2].table, > CharacterTableIsoclinic( poss[3].table ) ) ); true
The possible tables differ only w.r.t. the \(2\)-power map and perhaps the element orders. The Atlas prints the table of the split extension of \(M.G\), this table is one of the first two possibilities.
gap> List( poss, x -> PowerMap( x.table, 2 ) ); [ [ 1, 3, 1, 1, 3, 6, 8, 6, 4, 4, 4, 5, 16, 18, 16, 13, 15, 13, 19, 21, 19, 21, 1, 1, 6, 6, 9, 9, 11, 11, 16, 16, 13, 13 ], [ 1, 3, 1, 1, 3, 6, 8, 6, 4, 4, 4, 5, 16, 18, 16, 13, 15, 13, 19, 21, 19, 21, 1, 1, 6, 6, 11, 11, 9, 9, 16, 16, 13, 13 ], [ 1, 3, 1, 1, 3, 6, 8, 6, 4, 4, 4, 5, 16, 18, 16, 13, 15, 13, 19, 21, 19, 21, 3, 3, 8, 8, 9, 9, 11, 11, 18, 18, 15, 15 ], [ 1, 3, 1, 1, 3, 6, 8, 6, 4, 4, 4, 5, 16, 18, 16, 13, 15, 13, 19, 21, 19, 21, 3, 3, 8, 8, 11, 11, 9, 9, 18, 18, 15, 15 ] ]
The \(2\)-power map is not determined by the irreducible characters (and by the \(2\)-power map of the factor group \(2.L_3(4).2_3\)). We determine this map using the embedding of \(4_2.L_3(4).2_3\) into \(4.U_4(3).2_3\). Note that \(L_3(4).2_3\) is a maximal subgroup of \(U_4(3).2_3\) (see [CCN+85, p. 52]), and that the subgroup \(L_3(4)\) of \(U_4(3)\) lifts to \(4_2.L_3(4)\) in \(4.U_4(3)\) because no embedding of \(L_3(4)\), \(2.L_3(4)\), or \(4_1.L_3(4)\) into \(4.U_4(3)\) is possible.
gap> PossiblePowerMaps( poss[1].table, 2 ); [ [ 1, 3, 1, 1, 3, 6, 8, 6, 4, 4, 4, 5, 16, 18, 16, 13, 15, 13, 19, 21, 19, 21, 1, 1, 6, 6, 11, 11, 9, 9, 16, 16, 13, 13 ], [ 1, 3, 1, 1, 3, 6, 8, 6, 4, 4, 4, 5, 16, 18, 16, 13, 15, 13, 19, 21, 19, 21, 1, 1, 6, 6, 9, 9, 11, 11, 16, 16, 13, 13 ] ] gap> t:= CharacterTable( "4.U4(3)" );; gap> List( [ "L3(4)", "2.L3(4)", "4_1.L3(4)", "4_2.L3(4)" ], name -> > Length( PossibleClassFusions( CharacterTable( name ), t ) ) ); [ 0, 0, 0, 4 ]
So the split extension \(4_2.L_3(4).2_3\) of \(4_2.L_3(4)\) is a subgroup of the split extension \(4.U_4(3).2_3\) of \(4.U_4(3)\), and only one of the two possible tables of \(4_2.L_3(4).2_3\) admits a class fusion into the Atlas table of \(4.U_3(4).2_3\); the construction of the latter table is shown in Section 2.4-3.
gap> t2:= CharacterTable( "4.U4(3).2_3" );; gap> List( poss, x -> Length( PossibleClassFusions( x.table, t2 ) ) ); [ 0, 16, 0, 0 ]
I do not know a character theoretic argument that would disprove the existence of a group whose character table is the other candidate (or its isoclinic variant). For example, the table passes the tests from Section 2.4-17.
(It is straightforward to compute all extensions of \(4_2.L_3(4)\) by an automorphism of order two. The extensions with \(34\) conjugacy classes belong to the second candidate and its isoclinic variant.)
The correct table is the one that is contained in the GAP Character Table Library.
gap> IsRecord( TransformingPermutationsCharacterTables( poss[2].table, > lib ) ); true gap> ConstructModularMGATables( tblMG, tblGA, lib );;
In the construction of the character table of \(12_2.L_3(4).2_3\), the same ambiguity arises. We resolve it using the fact that \(4_2.L_3(4).2_3\) occurs as a factor group, modulo the unique normal subgroup of order three.
gap> tblMG := CharacterTable( "12_2.L3(4)" );; gap> tblG := CharacterTable( "6.L3(4)" );; gap> tblGA := CharacterTable( "6.L3(4).2_3" );; gap> name := "new12_2.L3(4).2_3";; gap> lib := CharacterTable( "12_2.L3(4).2_3" );; gap> poss := ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib );; #E 4 possibilities for new12_2.L3(4).2_3 gap> Length( poss ); 4 gap> nsg:= ClassPositionsOfNormalSubgroups( poss[1].table ); [ [ 1 ], [ 1, 5 ], [ 1, 7 ], [ 1, 4 .. 7 ], [ 1, 3 .. 7 ], [ 1 .. 7 ], [ 1 .. 50 ], [ 1 .. 62 ] ] gap> List( nsg, x -> Sum( SizesConjugacyClasses( poss[1].table ){ x } ) ); [ 1, 3, 2, 4, 6, 12, 241920, 483840 ] gap> factlib:= CharacterTable( "4_2.L3(4).2_3" );; gap> List( poss, x -> IsRecord( TransformingPermutationsCharacterTables( > x.table / [ 1, 5 ], factlib ) ) ); [ false, true, false, false ] gap> IsRecord( TransformingPermutationsCharacterTables( poss[2].table, > lib ) ); true gap> ConstructModularMGATables( tblMG, tblGA, lib );;
In the construction of the character table of \(M.G.A = 12_1.U_4(3).2_2'\) from the tables of \(M.G = 12_1.U_4(3)\) and \(G.A = 2.U_4(3).2_2'\), the action of \(A\) on the classes of \(M.G\) is uniquely determined, but we get two possible character tables.
(Note that the groups \(2.U_4(3).2_2\) and \(2.U_4(3).2_2'\) are isomorphic, but we have to take the latter one because the stored factor fusion from \(12_1.U_4(3)\) to \(2.U_4(3)\) must be combined with the class fusion from \(2.U_4(3)\) to \(2.U_4(3).2_2'\); using the library table of \(2.U_4(3).2_2\) would be technically more involved.)
gap> tblMG := CharacterTable( "12_1.U4(3)" );; gap> tblG := CharacterTable( "2.U4(3)" );; gap> tblGA := CharacterTable( "2.U4(3).2_2'" );; gap> name := "new12_1.U4(3).2_2'";; gap> lib := CharacterTable( "12_1.U4(3).2_2'" );; gap> poss := ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib );; #E 2 possibilities for new12_1.U4(3).2_2' gap> ConstructModularMGATables( tblMG, tblGA, lib );;
This is not surprising, the two tables involve the two isoclinic variants of \(4.U_4(3).2_2'\) (which is isomorphic with \(4.U_4(3).2_2\)) as tables of factor groups. The irreducible characters of the two tables are equal, only the \(2\)-power map and the element orders are different.
gap> Irr( poss[1].table ) = Irr( poss[2].table ); true gap> iso:= CharacterTableIsoclinic( poss[1].table );; gap> TransformingPermutationsCharacterTables( iso, poss[2].table ); rec( columns := (), group := <permutation group with 5 generators>, rows := () )
The same phenomenon occurs in the construction of the character table of \(M.G.A = 12_2.U_4(3).2_3'\) from the tables of \(M.G = 12_2.U_4(3)\) and \(G.A = 2.U_4(3).2_3'\).
gap> tblMG := CharacterTable( "12_2.U4(3)" );; gap> tblG := CharacterTable( "2.U4(3)" );; gap> tblGA := CharacterTable( "2.U4(3).2_3'" );; gap> name := "new12_2.U4(3).2_3'";; gap> lib := CharacterTable( "12_2.U4(3).2_3'" );; gap> poss := ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib );; #E 2 possibilities for new12_2.U4(3).2_3' gap> ConstructModularMGATables( tblMG, tblGA, lib );; gap> iso:= CharacterTableIsoclinic( poss[1].table );; gap> TransformingPermutationsCharacterTables( iso, poss[2].table ); rec( columns := (), group := <permutation group with 8 generators>, rows := () )
The list of Improvements to the Atlas of Finite Groups [BN95] states the following, concerning the group \(G = U_3(8)\).
There is a unique group of type \(3.G.6\) which contains the group of type \(3.G.3\) shown. But the (unique) groups of type \(3.G.6'\) and \(3.G.6''\) contain not this \(3.G.3\) but its isoclines.
In this section we will show that this statement is not correct, in the sense that the three isoclinic variants of groups of the structure \(3.U_3(8).3_1\) are in fact isomorphic.
As a consequence, there is a unique group of the structure \(3.U_3(8).6\), up to isomorphism. Note that otherwise the strange situation of nonisomorphic groups \(3.G.6\), \(3.G.6'\), and \(3.G.6''\) would happen, which would be also not isoclinic because their centres are trivial.
A group of the structure \(3.U_3(8).3_1\) can be obtained as the semidirect product \(G\), say, of the group SU\((3,8)\) with the automorphism of the field with \(64\) elements that raises each field element to its fourth power. Note that the semidirect product of SU\((3,8)\) with the field automorphism that squares each field element yields a group of the structure \(3.U_3(8).6\).
First we create a permutation representation of \(G\).
gap> s:= SU(3,8);; gap> gens:= GeneratorsOfGroup( s );; gap> imgs1:= List( gens, m -> List( m, v -> List( v, x -> x^4 ) ) );; gap> imgs2:= List( gens, m -> List( m, v -> List( v, x -> x^16 ) ) );; gap> f:= GF(64);; gap> mats:= List( gens, m -> IdentityMat( 9, f ) );; gap> for i in [ 1 .. Length( gens ) ] do > mats[i]{ [ 1 .. 3 ] }{ [ 1 .. 3 ] }:= gens[i]; > mats[i]{ [ 4 .. 6 ] }{ [ 4 .. 6 ] }:= imgs1[i]; > mats[i]{ [ 7 .. 9 ] }{ [ 7 .. 9 ] }:= imgs2[i]; > od; gap> fieldaut:= NullMat( 9, 9, f );; gap> fieldaut{ [ 4 .. 6 ] }{ [ 1 .. 3 ] }:= IdentityMat( 3, f );; gap> fieldaut{ [ 7 .. 9 ] }{ [ 4 .. 6 ] }:= IdentityMat( 3, f );; gap> fieldaut{ [ 1 .. 3 ] }{ [ 7 .. 9 ] }:= IdentityMat( 3, f );; gap> v:= [ 1, 0, 0, 1, 0, 0, 1, 0, 0 ] * One( f );; gap> g:= Group( Concatenation( mats, [ fieldaut ] ) );; gap> orb:= Orbit( g, v );; gap> Length( orb ); 32319 gap> act:= Action( g, orb );; gap> Size( act ) = 3 * Size( s ); true gap> sm:= SmallerDegreePermutationRepresentation( act );; gap> NrMovedPoints( Image( sm ) ); 4617 gap> g:= Image( sm );;
The next step is the construction of the central product of \(G\) and a cyclic group of order nine, of the structure \(3.(3 \times U_3(8).3_1)\). We could try to create the factor group of \(9 \times 3.U_3(8).3_1\) modulo a diagonal subgroup of order three, by just applying the / operation. Since GAP would need too much time for that, and since we know better in which situation we are, we create the desired action directly on suitable sets on pairs.
gap> c:= CyclicGroup( IsPermGroup, 9 );; gap> dp:= DirectProduct( g, c );; gap> u:= Image( Embedding( dp, 1 ) );; gap> c:= Image( Embedding( dp, 2 ) );; gap> c3:= c.1^3; (4618,4621,4624)(4619,4622,4625)(4620,4623,4626) gap> z:= Centre( u );; gap> Size( z ); Length( GeneratorsOfGroup( z ) ); 3 1 gap> diag:= Subgroup( dp, [ c3 * z.1 ] );; gap> orb:= Orbit( dp, [ 1, 4618 ], OnPairs );; gap> Length( orb ); 41553 gap> orb:= Set( orb );; gap> orbs:= List( OrbitsDomain( diag, orb, OnSets ), Set );; gap> Length( orbs ); 13851 gap> cp:= Action( dp, orbs, OnSetsSets );; gap> Size( cp ); 148925952
The three isoclinic variants of the structure \(3.U_3(8).3_1\) appear as subgroups of index three in this central product. (The fourth subgroup of index three is of course a central product of the structure \(3.(3 \times U_3(8))\).)
gap> der:= DerivedSubgroup( cp );; gap> Index( cp, der ); 9 gap> inter:= IntermediateSubgroups( cp, der ).subgroups;; gap> z:= Centre( cp );; gap> Size( z ); 9 gap> inter:= Filtered( inter, x -> not IsSubset( x, z ) );; gap> List( inter, Size ); [ 49641984, 49641984, 49641984 ]
Finally, we check that the three groups are isomorphic.
gap> IsomorphismGroups( inter[1], inter[2] ) <> fail; true gap> IsomorphismGroups( inter[1], inter[3] ) <> fail; true
Remark:
An indication that the groups might be isomorphic is the fact that their character tables are equivalent, which can be shown much easier, as follows.
gap> t1:= CharacterTable( "3.U3(8).3_1" );; gap> t2:= CharacterTableIsoclinic( t1, rec( k:= 1 ) );; gap> t3:= CharacterTableIsoclinic( t1, rec( k:= 2 ) );; gap> TransformingPermutationsCharacterTables( t1, t2 ) <> fail; true gap> TransformingPermutationsCharacterTables( t1, t3 ) <> fail; true
The sporadic simple group \(B\) contains a maximal subgroup \(\overline{N}\) of the type \((2^2 \times F_4(2)):2\), which is the normalizer of a 2C element \(\overline{x}\) in \(B\) (see [CCN+85, p. 217]).
We will see below that the normal Klein four group \(V\) in \(\overline{N}\) contains two 2A elements in \(B\). The 2A centralizer in \(B\), a group of the structure \(2.{}^2E_6(2).2\), contains maximal subgroups of the type \(2^2 \times F_4(2)\). So the two 2A type subgroups \(C_1\), \(C_2\) in \(V\) are conjugate in \(\overline{N}\), and \(Z = \langle x \rangle\) is the centre of \(\overline{N}\).
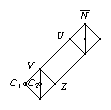
We start with computing the class fusion of the \(2^2 \times F_4(2)\) type subgroup \(U\) of \(\overline{N}\) into \(B\); in order to speed this up, we first compute the class fusion of the \(F_4(2)\) subgroup of \(U\) into \(B\) (which is unique), and use it and the stored embedding into \(U\) for prescribing an approximation of the desired class fusion. Additionally, we prescribe (without loss of generality) that the first involution class in \(V\) is mapped to the class 2C of \(B\).
gap> f42:= CharacterTable( "F4(2)" );; gap> v4:= CharacterTable( "2^2" );; gap> dp:= v4 * f42; CharacterTable( "V4xF4(2)" ) gap> b:= CharacterTable( "B" );; gap> f42fusb:= PossibleClassFusions( f42, b );; gap> Length( f42fusb ); 1 gap> f42fusdp:= GetFusionMap( f42, dp );; gap> comp:= CompositionMaps( f42fusb[1], InverseMap( f42fusdp ) ); [ 1, 3, 3, 3, 5, 6, 6, 7, 9, 9, 9, 9, 14, 14, 13, 13, 10, 14, 14, 12, 14, 17, 15, 18, 22, 22, 22, 22, 26, 26, 22, 22, 27, 27, 28, 31, 31, 39, 39, 36, 36, 33, 33, 39, 39, 35, 41, 42, 47, 47, 49, 49, 49, 58, 58, 56, 56, 66, 66, 66, 66, 58, 58, 66, 66, 69, 69, 60, 72, 72, 75, 79, 79, 81, 81, 85, 86, 83, 83, 91, 91, 94, 94, 104, 104, 109, 109, 116, 116, 114, 114, 132, 132, 140, 140 ] gap> v4fusdp:= GetFusionMap( v4, dp ); [ 1, 96 .. 286 ] gap> comp[ v4fusdp[2] ]:= 4;; gap> dpfusb:= PossibleClassFusions( dp, b, rec( fusionmap:= comp ) );; gap> Length( dpfusb ); 4 gap> Set( dpfusb, x -> x{ v4fusdp } ); [ [ 1, 4, 2, 2 ] ]
As announced above, we see that \(V\) contains two 2A involutions.
Set \(G = U / Z\), \(M.G = U\), and \(G.A = \overline{N} / Z\). The latter group is the direct product of \(F_4(2).2\) and a cyclic group of order \(2\). Next we compute the class fusion from \(G\) into \(G.A\).
gap> tblG:= dp / v4fusdp{ [ 1, 2 ] };; gap> tblMG:= dp;; gap> c2:= CharacterTable( "Cyclic", 2 );; gap> tblGA:= c2 * CharacterTable( "F4(2).2" ); CharacterTable( "C2xF4(2).2" ) gap> GfusGA:= PossibleClassFusions( tblG, tblGA );; gap> Length( GfusGA ); 4 gap> Length( RepresentativesFusions( tblG, GfusGA, tblGA ) ); 1
In principle, we have to be careful which of these equivalent maps we choose, since the underlying symmetries may be broken in the central extension \(M.G \rightarrow G\), for which we choose the default factor fusion.
However, in this situation the fusion \(G\) into \(G.A\) is unique already up to table automorphisms of the table of \(G.A\), so we are free to choose one map.
gap> Length( RepresentativesFusions( Group( () ), GfusGA, tblGA ) ); 1 gap> StoreFusion( tblG, GfusGA[1], tblGA );
The tables involved determine the character table of \(M.G.A \cong \overline{N}\) uniquely.
gap> elms:= PossibleActionsForTypeMGA( tblMG, tblG, tblGA );; gap> Length( elms ); 1 gap> poss:= PossibleCharacterTablesOfTypeMGA( tblMG, tblG, tblGA, elms[1], > "(2^2xF4(2)):2" );; gap> Length( poss ); 1 gap> tblMGA:= poss[1].table;;
Finally, we compare the table we constructed with the one that is contained in the GAP Character Table Library.
gap> IsRecord( TransformingPermutationsCharacterTables( tblMGA, > CharacterTable( "(2^2xF4(2)):2" ) ) ); true
The sporadic simple group \(B\) contains a maximal subgroup \(\overline{M}\) of type \(S_3 \times Fi_{22}.2\). In order to compute the character table of its preimage \(M\) in the Schur cover \(2.B\), we first analyse the structure of \(M\) and then describe the construction of the character table from known character tables.
Let \(Z\) denote the centre of \(2.B\). We start with \(\overline{M} = M/Z\). Its class fusion into \(B\) is uniquely determined by the character tables.
gap> s3:= CharacterTable( "Dihedral", 6 );; gap> fi222:= CharacterTable( "Fi22.2" );; gap> tblMbar:= s3 * fi222;; gap> b:= CharacterTable( "B" );; gap> Mbarfusb:= PossibleClassFusions( tblMbar, b );; gap> Length( Mbarfusb ); 1
The subgroup of type \(Fi_{22}\) lifts to the double cover \(2.Fi_{22}\) (that is, a group that is not a direct product \(2 \times Fi_{22}\)) in \(2.B\) since \(2.B\) admits no class fusion from \(Fi_{22}\).
gap> 2b:= CharacterTable( "2.B" );; gap> PossibleClassFusions( CharacterTable( "Fi22" ), 2b ); [ ]
So the preimage of \(Fi_{22}.2\) is one of the two nonisomorphic but isoclinic groups of type \(2.Fi_{22}.2\), and we have to decide which one really occurs. For that, we consider the subgroup of type \(3 \times Fi_{22}.2\) in \(B\), which is a 3A centralizer in \(B\). Its preimage has the structure \(3 \times 2.Fi_{22}.2\) because the preimage of the central group of order \(3\) is a cyclic group of order \(6\) and thus contains a normal complement of the \(2.Fi_{22}\) type subgroup. And a class fusion into \(2.B\) is possible only from the direct product containing the \(2.Fi_{22}.2\) group that is printed in the Atlas.
gap> c3:= CharacterTable( "Cyclic", 3 );; gap> 2fi222:= CharacterTable( "2.Fi22.2" );; gap> PossibleClassFusions( c3 * CharacterTableIsoclinic( 2fi222 ), 2b ); [ ]
Next we note that the involutions in the normal subgroup \(\overline{S}\) of type \(S_3\) in \(\overline{M}\) lift to involutions in \(2.B\).
gap> s3inMbar:= GetFusionMap( s3, tblMbar ); [ 1, 113 .. 225 ] gap> s3inb:= Mbarfusb[1]{ s3inMbar }; [ 1, 6, 2 ] gap> 2bfusb:= GetFusionMap( 2b, b );; gap> 2s3in2B:= InverseMap( 2bfusb ){ s3inb }; [ [ 1, 2 ], [ 8, 9 ], 3 ] gap> CompositionMaps( OrdersClassRepresentatives( 2b ), 2s3in2B ); [ [ 1, 2 ], [ 3, 6 ], 2 ]
Thus the preimage \(S\) of \(\overline{S}\) contains elements of order \(6\) but no elements of order \(4\), which implies that \(S\) is a direct product \(2 \times S_3\).
The two complements \(C_1\), \(C_2\) of \(Z\) in \(S\) are normal in the preimage \(N\) of \(\overline{N} = S_3 \times Fi_{22}\), which is thus of type \(S_3 \times 2.Fi_{22}\). However, they are conjugate under the action of \(2.Fi_{22}.2\), as no class fusion from \(S_3 \times 2.Fi_{22}.2\) into \(2.B\) is possible.
gap> PossibleClassFusions( s3 * 2fi222, 2b ); [ ]
(More specifically, the classes of element order \(36\) in \(2.Fi_{22}.2\) have centralizer orders \(36\) and \(72\), so their centralizer orders in \(S_3 \times 2.Fi_{22}.2\) are \(216\) and \(432\); but the centralizers of order \(36\) elements in \(2.B\) have centralizer order at most \(216\).)
Now let us see how the character table of \(M\) can be constructed.
Let \(Y\) denote the normal subgroup of order \(3\) in \(M\), and \(U\) its centralizer in \(M\), which has index \(2\) in \(M\). Then the character table of \(M\) is determined by the tables of \(M/Y\), \(U\), \(U/Y \cong 2.Fi_{22}.2\), and the action of \(M\) on the classes of \(U\).
As for \(M/Y\), consider the normal subgroup \(N = N_M(C_1)\) of index \(2\) in \(M\). In particular, \(S/Y\) is central in \(N/Y\) but not in \(M/Y\), so the character table of \(M/Y\) is determined by the tables of \(M/(YZ)\), \(N/Y \cong 2 \times 2.Fi_{22}\), \(N/(YZ) \cong 2 \times Fi_{22}\), and the action of \(M/Y\) on the classes of \(N/Y\).
Thus we proceed in two steps, starting with the computation of the character table of \(M/Y\), for which we choose the name according to the structure \(2^2.Fi_{22}.2\).
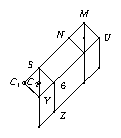
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> 2fi22:= CharacterTable( "2.Fi22" );; gap> tblNmodY:= c2 * 2fi22;; gap> centre:= GetFusionMap( 2fi22, tblNmodY ){ > ClassPositionsOfCentre( 2fi22 ) }; [ 1, 2 ] gap> tblNmod6:= tblNmodY / centre;; gap> tblMmod6:= c2 * fi222;; gap> fus:= PossibleClassFusions( tblNmod6, tblMmod6 );; gap> Length( fus ); 1 gap> StoreFusion( tblNmod6, fus[1], tblMmod6 ); gap> elms:= PossibleActionsForTypeMGA( tblNmodY, tblNmod6, tblMmod6 );; gap> Length( elms ); 1 gap> poss:= PossibleCharacterTablesOfTypeMGA( tblNmodY, tblNmod6, tblMmod6, > elms[1], "2^2.Fi22.2" );; gap> Length( poss ); 1 gap> tblMmodY:= poss[1].table; CharacterTable( "2^2.Fi22.2" )
So we found a unique solution for the character table of \(M/Y\). Now we compute the table of \(M\). For that, we have to specify the class fusion of \(U/Y\) into \(M/Y\); it is unique up to table automorphisms of \(M/Y\).
gap> tblU:= c3 * 2fi222;; gap> tblUmodY:= tblU / GetFusionMap( c3, tblU );; gap> fus:= PossibleClassFusions( tblUmodY, tblMmodY );; gap> Length( RepresentativesFusions( Group( () ), fus, tblMmodY ) ); 1 gap> StoreFusion( tblUmodY, fus[1], tblMmodY ); gap> elms:= PossibleActionsForTypeMGA( tblU, tblUmodY, tblMmodY );; gap> Length( elms ); 1 gap> poss:= PossibleCharacterTablesOfTypeMGA( tblU, tblUmodY, tblMmodY, > elms[1], "(S3x2.Fi22).2" );; gap> Length( poss ); 1 gap> tblM:= poss[1].table; CharacterTable( "(S3x2.Fi22).2" ) gap> mfus2b:= PossibleClassFusions( tblM, 2b );; gap> Length( RepresentativesFusions( tblM, mfus2b, 2b ) ); 1
We did not construct \(M\) as a central extension of \(\overline{M}\), so we verify that the tables fit together; note that this way we get also the class fusion from \(M\) onto \(\overline{M}\).
gap> Irr( tblM / ClassPositionsOfCentre( tblM ) ) = Irr( tblMbar ); true
Finally, we compare the table we constructed with the one that is contained in the GAP Character Table Library.
gap> IsRecord( TransformingPermutationsCharacterTables( tblM, > CharacterTable( "(S3x2.Fi22).2" ) ) ); true
The automorphism group \(Fi_{24}\) of the sporadic simple group \(Fi_{24}^{\prime}\) contains a maximal subgroup \(N\) of the type \((2 \times 2.Fi_{22}):2\), whose intersection with \(Fi_{24}^{\prime}\) is \(2.Fi_{22}.2\) (see [CCN+85, p. 207]).
The normal Klein four group \(V\) in \(N\) contains two 2C elements in \(Fi_{24}\), because the 2C centralizer in \(Fi_{24}\), a group of the structure \(2 \times Fi_{23}\), contains maximal subgroups of the type \(2 \times 2.Fi_{22}\), and so the two 2C type subgroups \(C_1\), \(C_2\) in \(V\) are conjugate in \(N\), and \(Z = Z(N)\) is the centre of \(N \cap Fi_{24}^{\prime}\).
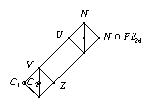
With \(U = C_N(C_1)\), a group of the type \(2 \times 2.Fi_{22}\), we set \(G = U / Z\), \(M.G = U\), and \(G.A = N / Z\). The latter group is the direct product of \(Fi_{22}.2\) and a cyclic group of order \(2\).
This is exactly the situation of the construction of the character table of the group that is called \(2^2.Fi_{22}.2\) in Section 2.4-9, where this group occurs as \(M/Y\)
. Since the character table is uniquely determined by the input data, it is the table we are interested in here.
So all we have to do is to compute the class fusion from this table into that of \(Fi_{24}\).
gap> fi24:= CharacterTable( "Fi24" );; gap> t:= CharacterTable( "2^2.Fi22.2" );; gap> fus:= PossibleClassFusions( t, fi24 );; gap> Length( fus ); 4 gap> Length( RepresentativesFusions( t, fus, fi24 ) ); 1
(It should be noted that we did not need the character table of the \(2.Fi_{22}.2\) type subgroup of \(N\) in the above construction, only the tables of \(2.Fi_{22}\) and \(Fi_{22}.2\) were used.)
The fact that the character table of a factor of a subgroup of \(2.B\) occurs as the character table of a subgroup of \(Fi_{24}\) is not a coincidence. In fact, the groups \(3.Fi_{24}\) and \(2.B\) are subgroups of the Monster group \(M\), and the subgroup \(U = 2.(S_3 \times Fi_{22}.2)\) of \(2.B\) normalizes an element of order three. The full normalizer of this element in \(M\) is \(3.Fi_{24}\), which means that we have established \(U\) as a (maximal) subgroup of \(3.Fi_{24}\). Note that we have constructed the character table of \(U\) in Section 2.4-9.
Let us compute the class fusion of \(U\) into \(3.Fi_{24}\).
gap> t:= CharacterTable( "(S3x2.Fi22).2" );; gap> 3fi24:= CharacterTable( "3.Fi24" );; gap> fus:= PossibleClassFusions( t, 3fi24 );; gap> Length( fus ); 16 gap> Length( RepresentativesFusions( t, fus, 3fi24 ) ); 1 gap> GetFusionMap( t, 3fi24 ) in fus; true
Moreover, \(U\) turns out to be the full normalizer of a 6A element in \(M\),
gap> m:= CharacterTable( "M" );; gap> tfusm:= PossibleClassFusions( t, m );; gap> Length( tfusm ); 4 gap> Length( RepresentativesFusions( t, tfusm, m ) ); 1 gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = 6 ); [ [ 1, 2, 142, 143 ] ] gap> Set( tfusm, x -> x{ nsg[1] } ); [ [ 1, 2, 4, 13 ] ] gap> OrdersClassRepresentatives( t ){ nsg[1] }; [ 1, 2, 3, 6 ] gap> PowerMap( m, -1 )[13]; 13 gap> Size( t ) = 2 * SizesCentralizers( m )[13]; true
(Thus \(U\) is also the full normalizer of an element of order six in \(2.B\) and in \(3.Fi_{24}\).)
The sporadic simple Fischer group \(Fi_{22}\) contains a maximal subgroup \(\overline{M}\) of type \(S_3 \times U_4(3).2_2\) (see [CCN+85, p. 163]). We claim that the preimage \(M\) of \(\overline{M}\) in the central extension \(2.Fi_{22}\) has the structure \(S_3 \times 2.U_4(3).2_2\), where the factor of type \(2.U_4(3).2_2\) is the one printed in the Atlas.
For that, we first note that the normal subgroup \(\overline{S}\) of type \(S_3\) in \(\overline{M}\) lifts to a group \(S\) which has the structure \(2 \times S_3\). This follows from the fact that all involutions in \(Fi_{22}\) lift to involutions in \(2.Fi_{22}\) or, equivalently, the central involution in \(2.Fi_{22}\) is not a square.
gap> 2Fi22:= CharacterTable( "2.Fi22" );; gap> ClassPositionsOfCentre( 2Fi22 ); [ 1, 2 ] gap> 2 in PowerMap( 2Fi22, 2 ); false
Second, the normal subgroup \(\overline{U} \cong U_4(3).2_2\) of \(Fi_{22}\) lifts to a nonsplit extension \(U\) in \(2.Fi_{22}\), since \(2.Fi_{22}\) contains no \(U_4(3)\) type subgroup. Furthermore, \(U\) is the \(2.U_4(3).2_2\) type group printed in the Atlas because the isoclinic variant does not admit a class fusion into \(2.Fi_{22}\).
gap> PossibleClassFusions( CharacterTable( "U4(3)" ), 2Fi22 ); [ ] gap> tblU:= CharacterTable( "2.U4(3).2_2" );; gap> iso:= CharacterTableIsoclinic( tblU ); CharacterTable( "Isoclinic(2.U4(3).2_2)" ) gap> PossibleClassFusions( iso, 2Fi22 ); [ ]
Now there are just two possibilities. Either the two \(S_3\) type subgroups in \(S\) are normal in \(M\) (and thus \(M\) is the direct product of any such \(S_3\) with the preimage of the \(U_4(3).2_2\) type subgroup), or they are conjugate in \(M\).
Suppose we are in the latter situation, let \(z\) be a generator of the centre of \(2.Fi_{22}\), and let \(\tau\), \(\sigma\) be an involution and an order three element respectively, in one of the \(S_3\) type subgroups.
Each element \(g \in U \setminus U^{\prime}\) conjugates \(\tau\) to an involution in the other \(S_3\) type subgroup of \(S\), so \(g^{-1} \tau g = \tau \sigma^{i} z\) for some \(i \in \{ 0, 1, 2 \}\). Furthermore, it is possible to choose \(g\) as an involution.
gap> derpos:= ClassPositionsOfDerivedSubgroup( tblU );; gap> outer:= Difference( [ 1 .. NrConjugacyClasses( tblU ) ], derpos );; gap> 2 in OrdersClassRepresentatives( tblU ){ outer }; true
With this choice, \((g \tau)^2 = \tau \sigma^{i} z \tau = \sigma^{-i} z\) holds, which means that \((g \tau)^3\) squares to \(z\). As we have seen above, this is impossible, hence \(M\) is a direct product, as claimed.
The class fusion of \(M\) into \(2.Fi_{22}\) is determined by the character tables, up to table automorphisms.
gap> tblM:= CharacterTable( "Dihedral", 6 ) * tblU;; gap> fus:= PossibleClassFusions( tblM, 2Fi22 );; gap> Length( RepresentativesFusions( tblM, fus, 2Fi22 ) ); 1 gap> IsRecord( TransformingPermutationsCharacterTables( tblM, > CharacterTable( "2.Fi22M8" ) ) ); true
The maximal subgroup \(U\) of type \(2.HS.2\) in the sporadic simple group \(HN\) extends to a group \(N\) of structure \(4.HS.2\) in the automorphism group \(HN.2\) of \(HN\) (see [CCN+85, p. 166]).
\(N\) is the normalizer of a 4D element \(g \in HN.2 \setminus HN\). The centralizer \(C\) of \(g\) is of type \(4.HS\), which is the central product of \(2.HS\) and the cyclic group \(\langle g \rangle\) of order \(4\). We have \(Z = Z(N) = \langle g^2 \rangle\). Since \(U/Z \cong HS.2\) is a complement of \(\langle g \rangle / Z\) in \(N/Z\), the factor group \(N/Z\) is a direct product of \(HS.2\) and a cyclic group of order \(2\).
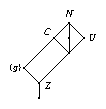
Thus \(N\) has the structure \(2.G.2\), the normal subgroup \(2.G\) being \(C\), the factor group \(G.2\) being \(2 \times HS.2\), and \(G\) being \(2 \times HS\). Each element in \(N \setminus C\) inverts \(g\), so \(N\) acts fixed point freely on the faithful irreducible characters of \(C\). Hence we can use PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) for constructing the character table of \(N\) from the tables of \(C\) and \(N/Z\) and the action of \(N\) on the classes of \(C\).
We start with the table of the central product \(C\). It can be viewed as an isoclinic table of the direct product of \(2.HS\) and a cyclic group of order \(2\), see 2.2-4.
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> tblC:= CharacterTableIsoclinic( CharacterTable( "2.HS" ) * c2 );;
The table of \(G\) is given as that of the factor group by the unique normal subgroup of \(C\) that consists of two conjugacy classes.
gap> ord2:= Filtered( ClassPositionsOfNormalSubgroups( tblC ), > x -> Length( x ) = 2 ); [ [ 1, 3 ] ] gap> tblCbar:= tblC / ord2[1];;
Finally, we construct the table of the extension \(G.2\) and the class fusion of \(G\) into this table (which is uniquely determined by the character tables).
gap> tblNbar:= CharacterTable( "HS.2" ) * c2;; gap> fus:= PossibleClassFusions( tblCbar, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 29, 30, 31, 32, 33, 34, 35, 36, 35, 36, 37, 38, 39, 40, 41, 42, 41, 42 ] ] gap> StoreFusion( tblCbar, fus[1], tblNbar );
Now we compute the table automorphisms of the table of \(C\) that are compatible with the extension \(N\); we get two solutions.
gap> elms:= PossibleActionsForTypeMGA( tblC, tblCbar, tblNbar ); [ [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6, 8 ], [ 7 ], [ 9 ], [ 10 ], [ 11 ], [ 12, 14 ], [ 13 ], [ 15 ], [ 16, 18 ], [ 17 ], [ 19 ], [ 20 ], [ 21 ], [ 22 ], [ 23 ], [ 24, 26 ], [ 25 ], [ 27 ], [ 28, 30 ], [ 29 ], [ 31 ], [ 32, 34 ], [ 33 ], [ 35 ], [ 36, 38 ], [ 37 ], [ 39 ], [ 40, 42 ], [ 41 ], [ 43 ], [ 44, 46 ], [ 45 ], [ 47 ], [ 48, 50 ], [ 49 ], [ 51, 53 ], [ 52, 54 ], [ 55 ], [ 56, 58 ], [ 57 ], [ 59 ], [ 60 ], [ 61, 65 ], [ 62, 68 ], [ 63, 67 ], [ 64, 66 ], [ 69 ], [ 70, 72 ], [ 71 ], [ 73 ], [ 74, 76 ], [ 75 ], [ 77, 81 ], [ 78, 84 ], [ 79, 83 ], [ 80, 82 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6, 8 ], [ 7 ], [ 9 ], [ 10 ], [ 11 ], [ 12, 14 ], [ 13 ], [ 15, 17 ], [ 16 ], [ 18 ], [ 19 ], [ 20 ], [ 21 ], [ 22 ], [ 23 ], [ 24, 26 ], [ 25 ], [ 27 ], [ 28, 30 ], [ 29 ], [ 31 ], [ 32, 34 ], [ 33 ], [ 35, 37 ], [ 36 ], [ 38 ], [ 39 ], [ 40, 42 ], [ 41 ], [ 43 ], [ 44, 46 ], [ 45 ], [ 47, 49 ], [ 48 ], [ 50 ], [ 51, 53 ], [ 52, 54 ], [ 55 ], [ 56, 58 ], [ 57 ], [ 59 ], [ 60 ], [ 61, 65 ], [ 62, 68 ], [ 63, 67 ], [ 64, 66 ], [ 69, 71 ], [ 70 ], [ 72 ], [ 73 ], [ 74, 76 ], [ 75 ], [ 77, 83 ], [ 78, 82 ], [ 79, 81 ], [ 80, 84 ] ] ]
We compute the possible character tables arising from these two actions.
gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblCbar, tblNbar, pi, "4.HS.2" ) );; gap> List( poss, Length ); [ 0, 2 ]
So one of the two table automorphisms turned out to be impossible; the reason is that the corresponding character table
would not admit a \(2\)-power map. (Alternatively, we could exclude this action on \(C\) by the fact that it is not compatible with the action of \(2.HS.2\) on its subgroup \(2.HS\), which occurs here as the restriction of the action of \(N\) on \(C\) to that of \(U\) on \(C \cap U\).)
The other table automorphism leads to two possible character tables. This is not surprising since \(N\) contains a subgroup of type \(2.HS.2\), and the above setup does not determine which of the two isoclinism types of this group occurs. Let us look at the possible class fusions from these tables into that of \(HN.2\):
gap> result:= poss[2];; gap> hn2:= CharacterTable( "HN.2" );; gap> possfus:= List( result, r -> PossibleClassFusions( r.table, hn2 ) );; gap> List( possfus, Length ); [ 32, 0 ] gap> RepresentativesFusions( result[1].table, possfus[1], hn2 ); [ [ 1, 46, 2, 2, 47, 3, 7, 45, 4, 58, 13, 6, 46, 47, 6, 47, 7, 48, 10, 62, 20, 9, 63, 21, 12, 64, 24, 27, 49, 50, 13, 59, 14, 16, 70, 30, 18, 53, 52, 17, 54, 20, 65, 22, 36, 56, 26, 76, 39, 77, 28, 59, 58, 31, 78, 41, 34, 62, 35, 65, 2, 45, 3, 45, 6, 48, 7, 47, 17, 54, 13, 49, 13, 50, 14, 50, 18, 53, 18, 52, 21, 56, 25, 57, 27, 59, 30, 60, 44, 72, 34, 66, 35, 66, 41, 71 ] ]
Only one of the candidates admits an embedding, and the class fusion is unique up to table automorphisms. So we are done.
Finally, we compare the table we have constructed with the one that is contained in the GAP Character Table Library.
gap> libtbl:= CharacterTable( "4.HS.2" );; gap> IsRecord( TransformingPermutationsCharacterTables( result[1].table, > libtbl ) ); true
(The following paragraphs have been added in May 2006.)
The Brauer tables of \(N = 2.G.2\) can be constructed as in Section 2.4-3. Note that the Brauer tables of \(C = 2.G\) and of \(N / Z = G.2\) are automatically available because the ordinary tables constructed above arose as a direct product and as an isoclinic table of a direct product, and the GAP Character Table Library contains the Brauer tables of the direct factors involved.
gap> StoreFusion( tblC, result[1].MGfusMGA, result[1].table ); gap> ForAll( PrimeDivisors( Size( result[1].table ) ), > p -> IsRecord( TransformingPermutationsCharacterTables( > BrauerTableOfTypeMGA( tblC mod p, tblNbar mod p, > result[1].table ).table, libtbl mod p ) ) ); true
Here it is advantageous that the Brauer table of \(C / Z = G\) is not needed in the construction, since GAP does not know how to compute the \(p\)-modular table of the ordinary table of \(G\) constructed above. Of course we have \(G \cong 2 \times HS\), and the \(p\)-modular table of \(HS\) is known, but in the construction of the table of \(G\) as a factor of the table of \(2.G\), the information is missing that the nonsolvable simple direct factor of \(2.G\) corresponds to the library table of \(HS\).
For the broken box
cases in the Atlas (see [CCN+85, p. xxiv]), the character tables can be constructed with the \(M.G.A\) construction method from Section 2.3-1. (The situation with \(9.U_3(8).3_3\) is more complicated, this group will be considered in Section 2.4-16.)
The group \(N = 4.A_6.2_3\) (see [CCN+85, p. 5]) can be described as an upward extension of the normal subgroup \(C \cong 4.A_6\) –which is a central product of \(U = 2.A_6\) and a cyclic group \(\langle g \rangle\) of order \(4\)– by a cyclic group of order \(2\), such that the factor group of \(N\) by the central subgroup \(Z = \langle g^2 \rangle\) of order \(2\) is isomorphic to a subdirect product \(\overline{N}\) of \(M_{10} = A_6.2_3\) and a cyclic group of order \(4\) and that \(N\) acts nontrivially on its normal subgroup \(\langle g \rangle\).
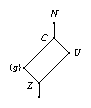
Thus \(N\) has the structure \(2.G.2\), with \(2.G = C\) and \(G.2 = \overline{N}\). These two groups are isoclinic variants of \(2 \times 2.A_6\) and of \(2 \times M_{10}\), respectively. Each element in \(N \setminus C\) inverts \(g\), so it acts fixed point freely on the faithful irreducible characters of \(C\). Hence we can use PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) for constructing the character table of \(N\) from the tables of \(C\) and \(N/Z\) and the action of \(N\) on the classes of \(C\).
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> 2a6:= CharacterTable( "2.A6" );; gap> tblC:= CharacterTableIsoclinic( 2a6 * c2 );; gap> ord2:= Filtered( ClassPositionsOfNormalSubgroups( tblC ), > x -> Length( x ) = 2 ); [ [ 1, 3 ] ] gap> tblG:= tblC / ord2[1];; gap> tblNbar:= CharacterTableIsoclinic( CharacterTable( "A6.2_3" ) * c2 );; gap> fus:= PossibleClassFusions( tblG, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 5, 6, 7, 8, 9, 10, 9, 10 ] ] gap> StoreFusion( tblG, fus[1], tblNbar ); gap> elms:= PossibleActionsForTypeMGA( tblC, tblG, tblNbar ); [ [ [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ], [ 6 ], [ 7, 11 ], [ 8, 12 ], [ 9, 13 ], [ 10, 14 ], [ 15, 17 ], [ 16, 18 ], [ 19, 23 ], [ 20, 24 ], [ 21, 25 ], [ 22, 26 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6 ], [ 7, 11 ], [ 8, 14 ], [ 9, 13 ], [ 10, 12 ], [ 15 ], [ 16, 18 ], [ 17 ], [ 19, 23 ], [ 20, 26 ], [ 21, 25 ], [ 22, 24 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6 ], [ 7, 11 ], [ 8, 14 ], [ 9, 13 ], [ 10, 12 ], [ 15, 17 ], [ 16 ], [ 18 ], [ 19, 23 ], [ 20, 26 ], [ 21, 25 ], [ 22, 24 ] ] ] gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblG, tblNbar, pi, "4.A6.2_3" ) ); [ [ ], [ ], [ rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 9, 6, 9, 8, 7, 10, 11, 10, 12, 13, 14, 15, 16, 13, 16, 15, 14 ], table := CharacterTable( "4.A6.2_3" ) ) ] ]
So we get a unique solution. It coincides with the character table of \(4.A_6.2_3\) that is stored in the GAP Character Table Library.
gap> t:= poss[3][1].table;; gap> IsRecord( TransformingPermutationsCharacterTables( t, > CharacterTable( "4.A6.2_3" ) ) ); true
Note that the first two candidates for the action lead to tables that do not admit a \(2\)-power map. In fact the \(2\)-power map of the character table of \(4.A_6.2_3\) is not uniquely determined by the matrix of character values. However, the \(2\)-power map is unique up to automorphisms of this matrix; the function PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) takes this into account, and returns only representatives, in this case one table.
As is mentioned in the Atlas (see [CCN+85, Section 6.7]), the group \(\Gamma L(2,9)\) contains subgroups of the structure \(4.A_6.2_3\). We can find them as follows.
gap> g:= GammaL(2,9);; gap> phi:= IsomorphismPermGroup( g );; gap> img:= Image( phi );; gap> der:= DerivedSubgroup( img );; gap> derder:= DerivedSubgroup( der );; gap> Index( img, derder ); 16 gap> inter:= Filtered( IntermediateSubgroups( img, derder ).subgroups, > s -> Size( s ) = 4 * Size( derder ) and > IsCyclic( CommutatorFactorGroup( s ) ) and > Size( Centre( s ) ) = 2 );; gap> Length( inter ); 2 gap> ForAll( inter, x -> IsConjugate( img, inter[1], x ) ); true gap> IsRecord( TransformingPermutationsCharacterTables( t, > CharacterTable( inter[1] ) ) ); true
The Atlas states in [CCN+85, Section 6.7] that there is a group of the structure \(2^2.A_6.2_3\) that is isoclinic with \(4.A_6.2_3\). We construct also the character table of the \(2^2.A_6.2_3\) type group with the \(M.G.A\) construction method from Section 2.3-1.
The group \(N = 2^2.A_6.2_3\) can be described as an upward extension of the normal subgroup \(C \cong 2 \times 2.A_6\) by a cyclic group of order \(2\), such that the factor group of \(N\) by the central subgroup \(Z\) of order \(2\) that is contained in \(U = C' \cong 2.A_6\) is isomorphic to a subdirect product \(\overline{N}\) of \(M_{10} = A_6.2_3\) and a cyclic group of order \(4\) and that \(N\) acts nontrivially on the centre of \(C\), which is a Klein four group.
Thus \(N\) has the structure \(2.G.2\), with \(2.G = C\) and \(G.2 = \overline{N}\). These latter group is an isoclinic variant of \(2 \times M_{10}\), as in the construction of \(4.A_6.2_3\). Each element in \(N \setminus C\) swaps the two involutions in \(Z(C) \setminus Z\), so it acts fixed point freely on those irreducible characters of \(C\) whose kernels do not contain \(Z\). Hence we can use PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) for constructing the character table of \(N\) from the tables of \(C\) and \(N/Z\) and the action of \(N\) on the classes of \(C\).
gap> tblC:= 2a6 * c2;; gap> z:= GetFusionMap( 2a6, tblC ){ ClassPositionsOfCentre( 2a6 ) }; [ 1, 3 ] gap> tblG:= tblC / z;; gap> tblNbar:= CharacterTableIsoclinic( CharacterTable( "A6.2_3" ) * c2 );; gap> fus:= PossibleClassFusions( tblG, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 5, 6, 7, 8, 9, 10, 9, 10 ] ] gap> StoreFusion( tblG, fus[1], tblNbar ); gap> elms:= PossibleActionsForTypeMGA( tblC, tblG, tblNbar ); [ [ [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ], [ 6 ], [ 7, 11 ], [ 8, 12 ], [ 9, 13 ], [ 10, 14 ], [ 15, 17 ], [ 16, 18 ], [ 19, 23 ], [ 20, 24 ], [ 21, 25 ], [ 22, 26 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6 ], [ 7, 11 ], [ 8, 14 ], [ 9, 13 ], [ 10, 12 ], [ 15 ], [ 16, 18 ], [ 17 ], [ 19, 23 ], [ 20, 26 ], [ 21, 25 ], [ 22, 24 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6 ], [ 7, 11 ], [ 8, 14 ], [ 9, 13 ], [ 10, 12 ], [ 15, 17 ], [ 16 ], [ 18 ], [ 19, 23 ], [ 20, 26 ], [ 21, 25 ], [ 22, 24 ] ] ] gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblG, tblNbar, pi, "2^2.A6.2_3" ) ); [ [ ], [ ], [ rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 9, 6, 9, 8, 7, 10, 11, 10, 12, 13, 14, 15, 16, 13, 16, 15, 14 ], table := CharacterTable( "2^2.A6.2_3" ) ) ] ]
So we get a unique solution.
The group \(N = 12.A_6.2_3\) (see [CCN+85, p. 5]) can be described as an upward extension of the normal subgroup \(C \cong 12.A_6\) –which is a central product of \(U = 6.A_6\) and a cyclic group \(\langle g \rangle\) of order \(4\)– by a cyclic group of order \(2\), such that the factor group of \(N\) by the central subgroup \(Z = \langle g^2 \rangle\) of order \(2\) is isomorphic to a subdirect product \(\overline{N}\) of \(3.M_{10} = 3.A_6.2_3\) and a cyclic group of order \(4\) and that \(N\) acts nontrivially on its normal subgroup \(\langle g \rangle\).
Note that \(N\) has a central subgroup \(Y\), say, of order \(3\), so the situation here differs from that for groups of the type \(12.G.2\) with \(G\) one of \(L_3(4)\), \(U_4(3)\), where the action on the normal subgroup of order three is nontrivial.
Thus \(N\) has the structure \(2.G.2\), with \(2.G = C\) and \(G.2 = \overline{N}\). These two groups are isoclinic variants of \(2 \times 6.A_6\) and of \(2 \times 3.M_{10}\), respectively. Each element in \(N \setminus C\) inverts \(g\), so it acts fixed point freely on the faithful irreducible characters of \(C\). Hence we can use PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) for constructing the character table of \(N\) from the tables of \(C\) and \(N/Z\) and the action of \(N\) on the classes of \(C\).
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> tblC:= CharacterTableIsoclinic( CharacterTable( "6.A6" ) * c2 );; gap> ord2:= Filtered( ClassPositionsOfNormalSubgroups( tblC ), > x -> Length( x ) = 2 ); [ [ 1, 7 ] ] gap> tblG:= tblC / ord2[1];; gap> tblNbar:= CharacterTableIsoclinic( CharacterTable( "3.A6.2_3" ) * c2 );; gap> fus:= PossibleClassFusions( tblG, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 21, 22, 23, 24, 25, 26 ] , [ 1, 2, 5, 6, 3, 4, 7, 8, 11, 12, 9, 10, 13, 14, 13, 14, 15, 16, 19, 20, 17, 18, 21, 22, 25, 26, 23, 24, 21, 22, 25, 26, 23, 24 ] ] gap> rep:= RepresentativesFusions( Group( () ), fus, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 21, 22, 23, 24, 25, 26 ] ] gap> StoreFusion( tblG, rep[1], tblNbar ); gap> elms:= PossibleActionsForTypeMGA( tblC, tblG, tblNbar ); [ [ [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ], [ 6 ], [ 7 ], [ 8 ], [ 9 ], [ 10 ], [ 11 ], [ 12 ], [ 13 ], [ 14 ], [ 15 ], [ 16 ], [ 17 ], [ 18 ], [ 19, 23 ], [ 20, 24 ], [ 21, 25 ], [ 22, 26 ], [ 27, 33 ], [ 28, 34 ], [ 29, 35 ], [ 30, 36 ], [ 31, 37 ], [ 32, 38 ], [ 39, 51 ], [ 40, 52 ], [ 41, 53 ], [ 42, 54 ], [ 43, 55 ], [ 44, 56 ], [ 45, 57 ], [ 46, 58 ], [ 47, 59 ], [ 48, 60 ], [ 49, 61 ], [ 50, 62 ] ], [ [ 1 ], [ 2, 8 ], [ 3 ], [ 4, 10 ], [ 5 ], [ 6, 12 ], [ 7 ], [ 9 ], [ 11 ], [ 13 ], [ 14 ], [ 15 ], [ 16 ], [ 17 ], [ 18 ], [ 19, 23 ], [ 20, 26 ], [ 21, 25 ], [ 22, 24 ], [ 27 ], [ 28, 34 ], [ 29 ], [ 30, 36 ], [ 31 ], [ 32, 38 ], [ 33 ], [ 35 ], [ 37 ], [ 39, 51 ], [ 40, 58 ], [ 41, 53 ], [ 42, 60 ], [ 43, 55 ], [ 44, 62 ], [ 45, 57 ], [ 46, 52 ], [ 47, 59 ], [ 48, 54 ], [ 49, 61 ], [ 50, 56 ] ], [ [ 1 ], [ 2, 8 ], [ 3 ], [ 4, 10 ], [ 5 ], [ 6, 12 ], [ 7 ], [ 9 ], [ 11 ], [ 13 ], [ 14 ], [ 15 ], [ 16 ], [ 17 ], [ 18 ], [ 19, 23 ], [ 20, 26 ], [ 21, 25 ], [ 22, 24 ], [ 27, 33 ], [ 28 ], [ 29, 35 ], [ 30 ], [ 31, 37 ], [ 32 ], [ 34 ], [ 36 ], [ 38 ], [ 39, 51 ], [ 40, 58 ], [ 41, 53 ], [ 42, 60 ], [ 43, 55 ], [ 44, 62 ], [ 45, 57 ], [ 46, 52 ], [ 47, 59 ], [ 48, 54 ], [ 49, 61 ], [ 50, 56 ] ] ] gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblG, tblNbar, pi, "12.A6.2_3" ) ); [ [ ], [ ], [ rec( MGfusMGA := [ 1, 2, 3, 4, 5, 6, 7, 2, 8, 4, 9, 6, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 16, 19, 18, 17, 20, 21, 22, 23, 24, 25, 20, 26, 22, 27, 24, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 29, 36, 31, 38, 33, 40, 35, 30, 37, 32, 39, 34 ], table := CharacterTable( "12.A6.2_3" ) ) ] ]
So we get again a unique solution. It coincides with the character table that is stored in the GAP Character Table Library.
gap> IsRecord( TransformingPermutationsCharacterTables( poss[3][1].table, > CharacterTable( "12.A6.2_3" ) ) ); true
The construction of the character table of \(4.L_2(25).2_3\) is analogous to that of the table of \(4.A_6.2_3\). We get a unique table that coincides with the table in the GAP library.
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> tblC:= CharacterTableIsoclinic( CharacterTable( "2.L2(25)" ) * c2 );; gap> ord2:= Filtered( ClassPositionsOfNormalSubgroups( tblC ), > x -> Length( x ) = 2 ); [ [ 1, 3 ] ] gap> tblG:= tblC / ord2[1];; gap> tblNbar:= CharacterTableIsoclinic( CharacterTable( "L2(25).2_3" ) * c2 );; gap> fus:= PossibleClassFusions( tblG, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 10, 11, 12, 13, 14, 13, 14, 15, 16, 15, 16, 17, 18, 17, 18, 19, 20, 19, 20 ], [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 10, 11, 12, 13, 14, 13, 14, 17, 18, 17, 18, 19, 20, 19, 20, 15, 16, 15, 16 ], [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 10, 11, 12, 13, 14, 13, 14, 19, 20, 19, 20, 15, 16, 15, 16, 17, 18, 17, 18 ] ] gap> rep:= RepresentativesFusions( Group( () ), fus, tblNbar ); [ [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 10, 11, 12, 13, 14, 13, 14, 15, 16, 15, 16, 17, 18, 17, 18, 19, 20, 19, 20 ] ] gap> StoreFusion( tblG, rep[1], tblNbar ); gap> elms:= PossibleActionsForTypeMGA( tblC, tblG, tblNbar ); [ [ [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ], [ 6 ], [ 7 ], [ 8 ], [ 9 ], [ 10 ], [ 11, 13 ], [ 12, 14 ], [ 15, 19 ], [ 16, 20 ], [ 17, 21 ], [ 18, 22 ], [ 23, 25 ], [ 24, 26 ], [ 27, 33 ], [ 28, 34 ], [ 29, 31 ], [ 30, 32 ], [ 35, 39 ], [ 36, 40 ], [ 37, 41 ], [ 38, 42 ], [ 43, 47 ], [ 44, 48 ], [ 45, 49 ], [ 46, 50 ], [ 51, 55 ], [ 52, 56 ], [ 53, 57 ], [ 54, 58 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6 ], [ 7 ], [ 8, 10 ], [ 9 ], [ 11 ], [ 12, 14 ], [ 13 ], [ 15, 19 ], [ 16, 22 ], [ 17, 21 ], [ 18, 20 ], [ 23, 25 ], [ 24 ], [ 26 ], [ 27, 31 ], [ 28, 34 ], [ 29, 33 ], [ 30, 32 ], [ 35, 39 ], [ 36, 42 ], [ 37, 41 ], [ 38, 40 ], [ 43, 47 ], [ 44, 50 ], [ 45, 49 ], [ 46, 48 ], [ 51, 55 ], [ 52, 58 ], [ 53, 57 ], [ 54, 56 ] ], [ [ 1 ], [ 2, 4 ], [ 3 ], [ 5 ], [ 6 ], [ 7 ], [ 8, 10 ], [ 9 ], [ 11, 13 ], [ 12 ], [ 14 ], [ 15, 19 ], [ 16, 22 ], [ 17, 21 ], [ 18, 20 ], [ 23, 25 ], [ 24 ], [ 26 ], [ 27, 33 ], [ 28, 32 ], [ 29, 31 ], [ 30, 34 ], [ 35, 39 ], [ 36, 42 ], [ 37, 41 ], [ 38, 40 ], [ 43, 47 ], [ 44, 50 ], [ 45, 49 ], [ 46, 48 ], [ 51, 55 ], [ 52, 58 ], [ 53, 57 ], [ 54, 56 ] ] ] gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblG, tblNbar, pi, "4.L2(25).2_3" ) ); [ [ ], [ ], [ rec( MGfusMGA := [ 1, 2, 3, 2, 4, 5, 6, 7, 8, 7, 9, 10, 9, 11, 12, 13, 14, 15, 12, 15, 14, 13, 16, 17, 16, 18, 19, 20, 21, 22, 21, 20, 19, 22, 23, 24, 25, 26, 23, 26, 25, 24, 27, 28, 29, 30, 27, 30, 29, 28, 31, 32, 33, 34, 31, 34, 33, 32 ], table := CharacterTable( "4.L2(25).2_3" ) ) ] ] gap> IsRecord( TransformingPermutationsCharacterTables( poss[3][1].table, > CharacterTable( "4.L2(25).2_3" ) ) ); true
Note that the group \(\Gamma L(2,25)\) does not contain subgroups of the structure \(4.L_2(25).2_3\), since \(\Gamma L(2,25)\) acts on its subgroup of scalar matrices via mapping each element to its fifth power, thus the central subgroup of order four in GL\((2,25)\) is central also in \(\Gamma L(2,25)\).
gap> g:= GammaL(2,25);; gap> phi:= IsomorphismPermGroup( g );; gap> img:= Image( phi );; gap> der:= DerivedSubgroup( img );; gap> derder:= DerivedSubgroup( der );; gap> Index( img, derder ); 48 gap> inter:= Filtered( IntermediateSubgroups( img, derder ).subgroups, > s -> Size( s ) = 4 * Size( derder ) and > IsCyclic( CommutatorFactorGroup( s ) ) and > Size( Centre( s ) ) = 2 ); [ ]
In order to construct a representation of a group of the structure \(4.L_2(25).2_3\), we can use the function CyclicExtensions from the GAP package GrpConst. We start from the index two subgroup \(4.L_2(25)\), which is a central product of \(SL(2,25)\) and a cyclic group of order four, and find exactly one upwards extension by a cyclic group of order two, up to isomorphism, with the required properties.
gap> c:= Centralizer( img, derder );; gap> Size( c ); IsCyclic( c ); 24 true gap> cgen:= MinimalGeneratingSet( c );; gap> four:= cgen[1]^6;; gap> s:= ClosureGroup( derder, four );; gap> LoadPackage( "GrpConst", false ); true gap> filt:= Filtered( CyclicExtensions( s, 2 ), > x -> Size( Centre( x ) ) = 2 and > IsCyclic( CommutatorFactorGroup( x ) ) );; gap> Length( filt ); 2 gap> IsomorphismGroups( filt[1], filt[2] ) <> fail; true
The character table of this group coincides with the library table.
gap> TransformingPermutationsCharacterTables( CharacterTable( filt[1] ), > CharacterTable( "4.L2(25).2_3" ) ) <> fail; true
The character tables of the simple group \(L_2(49)\) and of its extensions do not appear in the Atlas of Finite Groups [CCN+85], but they may be regarded as Atlas tables because a data file in the format used to produce the Atlas has been available for a long time, as is stated in [JLPW95, Appendix 2].
Analogous to \(L_2(9) \cong A_6\) and \(L_2(25)\), see Section 2.4-13, the Atlas map for \(G = L_2(49)\) shows a broken box
, since there is no group of the form \(2.G.2_3\), and a group of the structure \(4.G.2_3\) can be considered instead, which has a normal subgroup isomorphic with \(2.(2 \times G)\) and a factor group isomorphic with \((2 \times G).2_3\), see Section 2.4-13. Having its character table available has the effect that the functions DisplayAtlasMap (CTblLib: DisplayAtlasMap for the name of a simple group) and BrowseAtlasTable (CTblLib: BrowseAtlasTable) work with input "L2(49)".
We construct the character table of \(4.L_2(49).2_3\) in the same way as for the extensions of \(L_2(9)\) and \(L_2(25)\). There is a unique solution.
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> 2l:= CharacterTable( "2.L2(49)" );; gap> tblC:= CharacterTableIsoclinic( 2l * c2 );; gap> ord2:= Filtered( ClassPositionsOfNormalSubgroups( tblC ), > x -> Length( x ) = 2 ); [ [ 1, 3 ] ] gap> tblG:= tblC / ord2[1];; gap> tblNbar:= CharacterTableIsoclinic( > CharacterTable( "L2(49).2_3" ) * c2 );; gap> fus:= PossibleClassFusions( tblG, tblNbar );; gap> Length( fus ); 10 gap> StoreFusion( tblG, fus[1], tblNbar ); gap> elms:= PossibleActionsForTypeMGA( tblC, tblG, tblNbar );; gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblG, tblNbar, pi, "4.L2(49).2_3" ) );; gap> List( poss, Length ); [ 0, 0, 1 ] gap> t:= poss[3][1].table; CharacterTable( "4.L2(49).2_3" )
Analogous to the situation with \(L_2(9)\), a group of the desired structure can be found inside the semilinear group \(\Gamma\)L\((2,49)\). In fact, there is a unique class of subgroups in \(\Gamma\)L\((2,49)\) that contain SL\((2,49) \cong 2.G\), have the right order, have cyclic commutator factor group, and centre of order \(2\).
gap> g:= GammaL(2,49);; gap> phi:= IsomorphismPermGroup( g );; gap> img:= Image( phi );; gap> der:= DerivedSubgroup( img );; gap> derder:= DerivedSubgroup( der );; gap> Index( img, derder ); 96 gap> inter:= Filtered( IntermediateSubgroups( img, derder ).subgroups, > s -> Size( s ) = 4 * Size( derder ) and > IsCyclic( CommutatorFactorGroup( s ) ) and > Size( Centre( s ) ) = 2 );; gap> Length( inter ); 4 gap> ForAll( inter, x -> IsConjugate( img, inter[1], x ) ); true
The character tables of these groups coincide with the table constructed above, and with the library table.
gap> TransformingPermutationsCharacterTables( t, > CharacterTable( inter[1] ) ) <> fail; true gap> TransformingPermutationsCharacterTables( t, > CharacterTable( "4.L2(49).2_3" ) ) <> fail; true
We start with the character-theoretic construction of this table, analogous to the cases of \(L_2(9)\), \(L_2(25)\), \(L_2(49)\).
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> 2l:= CharacterTable( "2.L2(81)" );; gap> tblC:= CharacterTableIsoclinic( 2l * c2 );; gap> ord2:= Filtered( ClassPositionsOfNormalSubgroups( tblC ), > x -> Length( x ) = 2 ); [ [ 1, 3 ] ] gap> tblG:= tblC / ord2[1];; gap> tblNbar:= CharacterTableIsoclinic( > CharacterTable( "L2(81).2_3" ) * c2 );; gap> fus:= PossibleClassFusions( tblG, tblNbar );; gap> Length( fus ); 40 gap> fusreps:= RepresentativesFusions( tblG, fus, tblNbar );; gap> Length( fusreps ); 1 gap> StoreFusion( tblG, fusreps[1], tblNbar ); gap> elms:= PossibleActionsForTypeMGA( tblC, tblG, tblNbar );; gap> poss:= List( elms, pi -> PossibleCharacterTablesOfTypeMGA( > tblC, tblG, tblNbar, pi, "4.L2(81).2_3" ) );; gap> List( poss, Length ); [ 0, 0, 1 ] gap> TransformingPermutationsCharacterTables( poss[3][1].table, > CharacterTable( "4.L2(81).2_3" ) ) <> fail; true
Like in the case of \(L_2(25)\), there are no \(4.L_2(81).2_3\) type subgroups in \(\Gamma L(2,81)\).
gap> g:= GammaL(2,81);; gap> phi:= IsomorphismPermGroup( g );; gap> img:= Image( phi );; gap> der:= DerivedSubgroup( img );; gap> derder:= DerivedSubgroup( der );; gap> Index( img, derder ); 320 gap> inter:= Filtered( IntermediateSubgroups( img, derder ).subgroups, > s -> Size( s ) = 4 * Size( derder ) and > IsCyclic( CommutatorFactorGroup( s ) ) and > Size( Centre( s ) ) = 2 );; gap> ForAll( inter, x -> IsConjugate( img, inter[1], x ) ); true gap> NrConjugacyClasses( inter[1] ); 52 gap> NrConjugacyClasses( CharacterTable( "4.L2(81).2_3" ) ); 112
The subgroups of \(\Gamma L(2,81)\) constructed above have the structure \(2.L_2(81).4_1\).
gap> t:= CharacterTable( "2.L2(81).4_1" );; gap> NrConjugacyClasses( t ); 52 gap> TransformingPermutationsCharacterTables( t, > CharacterTable( inter[1] ) ) <> fail; true
Like in the case of \(L_2(25)\), we can construct a group with the structure \(4.L_2(81).2_3\) via the function CyclicExtensions from the GAP package GrpConst.
gap> c:= Centralizer( img, derder );; gap> Size( c ); IsCyclic( c ); 80 true gap> cgen:= MinimalGeneratingSet( c );; gap> four:= cgen[1]^20;; gap> s:= ClosureGroup( derder, four );; gap> LoadPackage( "GrpConst", false ); true gap> filt:= Filtered( CyclicExtensions( s, 2 ), > x -> Size( Centre( x ) ) = 2 and > IsCyclic( CommutatorFactorGroup( x ) ) );; gap> Length( filt ); 2 gap> IsomorphismGroups( filt[1], filt[2] ) <> fail; true gap> TransformingPermutationsCharacterTables( CharacterTable( filt[1] ), > CharacterTable( "4.L2(81).2_3" ) ) <> fail; true
The group that is called \(9.U_3(8).3_3\) in the Atlas of Finite Groups occurs as a subgroup of \(\Gamma\)U\((3, 8)\). Note that GU\((3, 8)\) has the structure \(3.(3 \times U_3(8)).3_2\) (see [CCN+85, p. 66]), and extending the subgroup \(C = 3.(3 \times U_3(8))\) by the product of an element outside \(C\) with the field automorphism of order three of GF\((64)\) yields a group \(N\) of the structure \(3.(3 \times U_3(8)).3_3\) whose centre has order three.
The character table of \(N\) can be constructed with the \(M.G.A\) construction method from Section 2.3-1. The situation is similar to that with \(4.A_6.2_3\), see Section 2.4-13, in particular the situation is described by the same picture that is shown for \(4.A_6.2_3\) in this section, just the subgroups \(Z\) and \(\langle g \rangle\) have the orders three and nine, respectively, and \(C\) has index three in \(N\).
The normal subgroup \(C \cong 9.U_3(8)\) is a central product of \(U = 3.U_3(8)\) and a cyclic group \(\langle g \rangle\) of order \(9\), and the factor group of \(N\) by the central subgroup \(Z = \langle g^3 \rangle\) of order \(3\) is isomorphic to a subdirect product \(\overline{N}\) of \(U_3(8).3_3\) and a cyclic group of order \(9\), such that \(N\) acts nontrivially on its normal subgroup \(\langle g \rangle\).
Thus \(N\) has the structure \(3.G.3\), with \(3.G = C\) and \(G.3 = \overline{N}\). Each element in \(N \setminus C\) raises \(g\) to its fourth or seventh power, so it acts fixed point freely on the faithful irreducible characters of \(C\). Hence we can use PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) for constructing the character table of \(N\) from the tables of \(C\) and \(N/Z\) and the action of \(N\) on the classes of \(C\).
Since we want to construct also Brauer tables of \(N\), we have to choose the class fusion that describes the embedding of \(C / Z\) into \(\overline{N}\) compatibly with the known Brauer tables of \(U_3(8)\) and \(U_3(8).3_3\). Note that the \(2\)-modular tables of these groups impose additional conditions on the class fusion.
gap> s:= CharacterTable( "U3(8)" );; gap> s3:= CharacterTable( "U3(8).3_3" );; gap> poss:= PossibleClassFusions( s, s3 );; gap> Length( poss ); 4 gap> Length( RepresentativesFusions( s, poss, s3 ) ); 1 gap> smod2:= s mod 2;; gap> s3mod2:= s3 mod 2;; gap> good:= [];; modmap:= 0;; gap> for map in poss do > modmap:= CompositionMaps( InverseMap( GetFusionMap( s3mod2, s3 ) ), > CompositionMaps( map, GetFusionMap( smod2, s ) ) ); > rest:= List( Irr( s3mod2 ), x -> x{ modmap } ); > if not fail in Decomposition( Irr( smod2 ), rest, "nonnegative" ) then > Add( good, map ); > fi; > od; gap> Length( good ); 2
The class fusion from \(U_3(8)\) to \(U_3(8).3_3\) is determined up to complex conjugation by the \(2\)-modular Brauer tables. We choose the fusion that is stored on the library tables.
gap> good[2] = CompositionMaps( PowerMap( s3, -1 ), good[1] ); true gap> GetFusionMap( s, s3 ) in good; true gap> sfuss3:= GetFusionMap( s, s3 );;
In the next step, we construct the character tables of \(C / Z \cong U_3(8) \times 3\) and \(N / Z \cong (U_3(8) \times 3).3_3\), and those class fusions between the two tables that are compatible with the fusion between the factors that was chosen above (w. r. t. the stored factor fusions).
In order not to leave out some candidates, we have to consider also the table of \(N/Z\) that is obtained from the other
construction as an isoclinic table of \(3 \times U_3(8).3_3\).
(This may look complicated. It would perhaps be more natural to construct the ordinary tables first, by considering the possible fusions, and later to adjust the choices to the conditions that are imposed by the Brauer tables. However, the technical complications of that construction would not be smaller in the end.)
We get four candidates, two for each of the two tables of \(N/Z\).
gap> c3:= CharacterTable( "Cyclic", 3 );; gap> tblG:= s * c3;; gap> dp:= s3 * c3;; gap> tblGA1:= CharacterTableIsoclinic( dp, rec( k:= 1 ) );; gap> tblGA2:= CharacterTableIsoclinic( dp, rec( k:= 2 ) );; gap> good:= [];; gap> tblGmod2:= tblG mod 2;; gap> for tblGA in [ tblGA1, tblGA2 ] do > tblGAmod2:= tblGA mod 2; > for map in PossibleClassFusions( tblG, tblGA ) do > modmap:= CompositionMaps( > InverseMap( GetFusionMap( tblGAmod2, tblGA ) ), > CompositionMaps( map, GetFusionMap( tblGmod2, tblG ) ) ); > rest:= List( Irr( tblGAmod2 ), x -> x{ modmap } ); > if not fail in Decomposition( Irr( tblGmod2 ), rest, > "nonnegative" ) and > CompositionMaps( GetFusionMap( tblGA, s3 ), map ) = > CompositionMaps( sfuss3, GetFusionMap( tblG, s ) ) then > Add( good, [ tblGA, map ] ); > fi; > od; > od; gap> List( good, x -> x[1] ); [ CharacterTable( "Isoclinic(U3(8).3_3xC3,1)" ), CharacterTable( "Isoclinic(U3(8).3_3xC3,1)" ), CharacterTable( "Isoclinic(U3(8).3_3xC3,2)" ), CharacterTable( "Isoclinic(U3(8).3_3xC3,2)" ) ]
The character table of \(C\) can be constructed with CharacterTableIsoclinic (Reference: CharacterTableIsoclinic) from the character table of \(3 \times 3.U_3(8)\). (Here we need to consider only one variant of the table.)
gap> 3s:= CharacterTable( "3.U3(8)" );; gap> dp:= 3s * c3;; gap> tblMG:= CharacterTableIsoclinic( dp );;
The construction of this table does not automatically yield a factor fusion to the table of \(C/Z\). We form the relevant factor table, which has the same ordering of irreducible characters, and use the factor fusion to this table.
gap> GetFusionMap( tblMG, tblG ); fail gap> cen:= ClassPositionsOfCentre( tblMG ); [ 1, 2, 3, 4, 5, 6, 7, 8, 9 ] gap> OrdersClassRepresentatives( tblMG ){ cen }; [ 1, 9, 9, 3, 9, 9, 3, 9, 9 ] gap> facttbl:= tblMG / [ 1, 4, 7 ];; gap> tr:= TransformingPermutationsCharacterTables( facttbl, tblG );; gap> tr.rows; tr.columns; () () gap> StoreFusion( tblMG, GetFusionMap( tblMG, facttbl ), tblG );
Now we compute the orbits of the possible actions of \(N\) on the classes of \(C\), and the resulting candidates for the character table of \(N\).
gap> posstbls:= [];; gap> for pair in good do > tblGA:= pair[1]; > GfusGA:= pair[2]; > tblG:= s * c3; > StoreFusion( tblG, GfusGA, tblGA ); > for pi in PossibleActionsForTypeMGA( tblMG, tblG, tblGA ) do > for cand in PossibleCharacterTablesOfTypeMGA( > tblMG, tblG, tblGA, pi, "test" ) do > Add( posstbls, [ tblGA, cand ] ); > od; > od; > od; gap> Length( posstbls ); 32
Now we discard all those candidates that are not compatible with the \(2\)-modular character tables.
gap> compatible:= [];; r:= 0;; modr:= 0;; gap> for pair in posstbls do > tblGA:= pair[1]; > r:= pair[2]; > comp:= ComputedClassFusions( tblMG ); > pos:= PositionProperty( comp, x -> x.name = Identifier( r.table ) ); > if pos = fail then > StoreFusion( tblMG, r.MGfusMGA, r.table ); > else > comp[ pos ]:= ShallowCopy( comp[ pos ] ); > comp[ pos ].map:= r.MGfusMGA; > fi; > Unbind( ComputedBrauerTables( tblMG )[2] ); > modr:= BrauerTableOfTypeMGA( tblMG mod 2, tblGA mod 2, r.table ); > rest:= List( Irr( modr.table ), x -> x{ modr.MGfusMGA } ); > dec:= Decomposition( Irr( tblMG mod 2 ), rest, "nonnegative" ); > if not fail in dec then > Add( compatible, pair ); > fi; > od; gap> Length( compatible ); 8
The remaining candidates fall into two equivalence classes.
gap> tbls:= [];; gap> for pair in compatible do > if ForAll( tbls, t -> TransformingPermutationsCharacterTables( > t, pair[2].table ) = fail ) then > Add( tbls, pair[2].table ); > fi; > od; gap> Length( tbls ); 2
The two tables can be distinguished by their element orders one contains the element order \(54\) and the other does not or by their \(4\)th power maps the classes of element order \(171\) in one table are not fixed by the \(4\)th power map, the corresponding classes in the other table are fixed.
gap> Set( OrdersClassRepresentatives( tbls[1] ) ); [ 1, 2, 3, 4, 6, 7, 9, 12, 18, 19, 21, 27, 36, 54, 57, 63, 171 ] gap> Set( OrdersClassRepresentatives( tbls[2] ) ); [ 1, 2, 3, 4, 6, 7, 9, 12, 18, 19, 21, 27, 36, 57, 63, 171 ] gap> pos171:= Positions( OrdersClassRepresentatives( tbls[1] ), 171 );; gap> pow4:= PowerMap( tbls[1], 4 );; gap> ForAny( [ 1 .. Length( pos171 ) ], > i -> pos171[i] = pow4[ pos171[i] ] ); false gap> pos171:= Positions( OrdersClassRepresentatives( tbls[2] ), 171 );; gap> PowerMap( tbls[2], 4 ){ pos171 } = pos171; true
Thus we can use the group \(N\) to decide which table is correct. For that, we construct a permutation representation of \(N\).
gap> gu:= GU(3,8);; gap> orbs:= OrbitsDomain( gu, Elements( GF(64)^3 ) );; gap> List( orbs, Length ); [ 1, 32319, 32832, 32832, 32832, 32832, 32832, 32832, 32832 ] gap> orb:= SortedList( First( orbs, x -> Length( x ) = 32319 ) );; gap> actgu:= Action( gu, orb, OnRight );; gap> Size( actgu ) = Size( gu ); true gap> cen:= Centre( actgu );; gap> Size( cen ); 9 gap> u:= ClosureGroup( DerivedSubgroup( actgu ), cen );; gap> aut:= v -> List( v, x -> x^4 );; gap> pi:= PermList( List( orb, v -> PositionSorted( orb, aut( v ) ) ) );; gap> outer:= First( GeneratorsOfGroup( actgu ), x -> not x in u );; gap> g:= ClosureGroup( u, pi * outer );;
Before we perform computations with the group, we reduce the degree of the representation by a factor of \(7\).
gap> g:= Group( SmallGeneratingSet( g ) );; gap> allbl:= AllBlocks( g );; gap> List( allbl, Length ); [ 3, 21, 63, 9, 7 ] gap> orb:= Orbit( g, First( allbl, x -> Length( x ) = 7 ), OnSets );; gap> act:= Action( g, orb, OnSets );; gap> Size( act ) = Size( g ); true gap> NrMovedPoints( act ); 4617
Now we test whether an element of order \(171\) in \(N\) is conjugate in \(N\) to its fourth power.
gap> repeat x:= PseudoRandom( act ); until Order( x ) = 171; gap> IsConjugate( act, x, x^4 ); true
This means that the second of the candidate tables constructed above is the right one. The character table with the identifier "9.U3(8).3_3" in the character table library is equivalent to this table.
gap> lib:= CharacterTable( "9.U3(8).3_3" );; gap> IsRecord( TransformingPermutationsCharacterTables( tbls[2], lib ) ); true
GAP's currently available methods for the automatic computation of character tables would require too much space when called with this permutation group. Using interactive methods, one can compute the character table with GAP. The table obtained this way is equivalent to the library character table with the identifier "9.U3(8).3_3".
I do not know how to disprove the other candidate with character-theoretic arguments. Thus this table provides an example of a pseudo character table, see Section 2.4-17.
With the construction method for character tables of groups of the type \(M.G.A\), one can construct tables that have many properties of character tables but that are not character tables of groups, cf. [Gag86]. For example, the group \(3.A_6.2_3\) has a central subgroup of order \(3\), so it is not of the type \(M.G.A\) with fixed-point free action on the faithful characters of \(M.G\).
However, if we apply the \(M.G.A\) construction
to the groups \(M.G = 3.A_6\), \(G = A_6\), and \(G.A = A_6.2_3\) then we get a (in this case unique) result.
gap> tblMG := CharacterTable( "3.A6" );; gap> tblG := CharacterTable( "A6" );; gap> tblGA := CharacterTable( "A6.2_3" );; gap> elms:= PossibleActionsForTypeMGA( tblMG, tblG, tblGA ); [ [ [ 1 ], [ 2, 3 ], [ 4 ], [ 5, 6 ], [ 7, 8 ], [ 9 ], [ 10, 11 ], [ 12, 15 ], [ 13, 17 ], [ 14, 16 ] ] ] gap> poss:= PossibleCharacterTablesOfTypeMGA( > tblMG, tblG, tblGA, elms[1], "pseudo" ); [ rec( MGfusMGA := [ 1, 2, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 10, 8, 10, 9 ], table := CharacterTable( "pseudo" ) ) ]
Such a table automatically satisfies the orthogonality relations, and the tensor product of two irreducible characters
of which at least one is a row from \(G.A\) decomposes into a sum of the irreducible characters
, where the coefficients are nonnegative integers.
In this example, any tensor product decomposes with nonnegative integral coefficients, \(n\)-th symmetrizations of irreducible characters
decompose, for \(n \leq 5\), and the class multiplication coefficients
are nonnegative integers.
gap> pseudo:= poss[1].table; CharacterTable( "pseudo" ) gap> Display( pseudo ); pseudo 2 4 3 4 3 . 3 2 . . . 2 3 3 3 3 3 1 1 2 1 1 1 1 1 . . . 5 1 1 . . . . . 1 1 1 . . . 1a 3a 2a 6a 3b 4a 12a 5a 15a 15b 4b 8a 8b 2P 1a 3a 1a 3a 3b 2a 6a 5a 15a 15b 2a 4a 4a 3P 1a 1a 2a 2a 1a 4a 4a 5a 5a 5a 4b 8a 8b 5P 1a 3a 2a 6a 3b 4a 12a 1a 3a 3a 4b 8b 8a X.1 1 1 1 1 1 1 1 1 1 1 1 1 1 X.2 1 1 1 1 1 1 1 1 1 1 -1 -1 -1 X.3 10 10 2 2 1 -2 -2 . . . . . . X.4 16 16 . . -2 . . 1 1 1 . . . X.5 9 9 1 1 . 1 1 -1 -1 -1 1 -1 -1 X.6 9 9 1 1 . 1 1 -1 -1 -1 -1 1 1 X.7 10 10 -2 -2 1 . . . . . . B -B X.8 10 10 -2 -2 1 . . . . . . -B B X.9 6 -3 -2 1 . 2 -1 1 A /A . . . X.10 6 -3 -2 1 . 2 -1 1 /A A . . . X.11 12 -6 4 -2 . . . 2 -1 -1 . . . X.12 18 -9 2 -1 . 2 -1 -2 1 1 . . . X.13 30 -15 -2 1 . -2 1 . . . . . . A = -E(15)-E(15)^2-E(15)^4-E(15)^8 = (-1-Sqrt(-15))/2 = -1-b15 B = E(8)+E(8)^3 = Sqrt(-2) = i2 gap> IsInternallyConsistent( pseudo ); true gap> irr:= Irr( pseudo );; gap> test:= Concatenation( List( [ 2 .. 5 ], > n -> Symmetrizations( pseudo, irr, n ) ) );; gap> Append( test, Set( Tensored( irr, irr ) ) ); gap> fail in Decomposition( irr, test, "nonnegative" ); false gap> if ForAny( Tuples( [ 1 .. NrConjugacyClasses( pseudo ) ], 3 ), > t -> not ClassMultiplicationCoefficient( pseudo, t[1], t[2], t[3] ) > in NonnegativeIntegers ) then > Error( "contradiction" ); > fi;
I do not know a character-theoretic argument for showing that this table is not the character table of a group, but we can use the following group-theoretic argument. Suppose that the group \(G\), say, has the above character table. Then \(G\) has a unique composition series with factors of the orders \(3\), \(360\), and \(2\), respectively. Let \(N\) denote the normal subgroup of order \(3\) in \(G\). The factor group \(F = G/N\) is an automorphic extension of \(A_6\), and according to [CCN+85, p. 4] it is isomorphic with \(M_{10} = A_6.2_3\) and has Sylow \(3\) normalizers of the structure \(3^2 : Q_8\). Since the Sylow \(3\) subgroup of \(G\) is a self-centralizing nonabelian group of order \(3^3\) and of exponent \(3\), the Sylow \(3\) normalizers in \(G\) have the structure \(3^{{1+2}}_+ : Q_8\), but the \(Q_8\) type subgroups of Aut\(( 3^{{1+2}}_+ )\) act trivially on the centre of \(3^{{1+2}}_+\), contrary to the situation in the above table.
In general, this construction need not produce tables for which all symmetrizations of irreducible characters decompose properly. For example, applying PossibleCharacterTablesOfTypeMGA (CTblLib: PossibleCharacterTablesOfTypeMGA) to the case \(M.G = 3.L_3(4)\) and \(G.A = L_3(4).2_1\) does not yield a table because the function suppresses tables that do not admit \(p\)-th power maps, for prime divisors \(p\) of the order of \(M.G.A\), and in this case no compatible \(2\)-power map exists.
gap> tblMG := CharacterTable( "3.L3(4)" );; gap> tblG := CharacterTable( "L3(4)" );; gap> tblGA := CharacterTable( "L3(4).2_1" );; gap> elms:= PossibleActionsForTypeMGA( tblMG, tblG, tblGA ); [ [ [ 1 ], [ 2, 3 ], [ 4 ], [ 5, 6 ], [ 7 ], [ 8 ], [ 9, 10 ], [ 11 ], [ 12, 13 ], [ 14 ], [ 15, 16 ], [ 17, 20 ], [ 18, 22 ], [ 19, 21 ], [ 23, 26 ], [ 24, 28 ], [ 25, 27 ] ] ] gap> PossibleCharacterTablesOfTypeMGA( tblMG, tblG, tblGA, elms[1], "?" ); [ ]
Also, it may happen that already PossibleActionsForTypeMGA (CTblLib: PossibleActionsForTypeMGA) returns an empty list. Examples are \(M.G = 3_1.U_4(3)\), \(G.A = U_4(3).2_2\) and \(M.G = 3_2.U_4(3)\), \(G.A = U_4(3).2_3\).
gap> tblG := CharacterTable( "U4(3)" );; gap> tblMG := CharacterTable( "3_1.U4(3)" );; gap> tblGA := CharacterTable( "U4(3).2_2" );; gap> PossibleActionsForTypeMGA( tblMG, tblG, tblGA ); [ ] gap> tblMG:= CharacterTable( "3_2.U4(3)" );; gap> tblGA:= CharacterTable( "U4(3).2_3" );; gap> PossibleActionsForTypeMGA( tblMG, tblG, tblGA ); [ ]
Also the sections 2.4-5 and 2.4-16 provide examples of pseudo character tables. If one does not use the arguments about Brauer tables then the latter section presents in fact several pseudo character tables.
For a group \(M.G.A\) in the sense of Section 2.3-1 such that not all ordinary irreducible characters \(\chi\) have the property that \(M\) is contained in the kernel of \(\chi\) or \(\chi\) is induced from \(M.G\), it may happen that there are primes \(p\) such that all irreducible \(p\)-modular characters have this property. This happens if and only if the preimages in \(M.G.A\) of each \(p\)-regular conjugacy class in \(G.A \setminus G\) form one conjugacy class.
The following function can be used to decide whether this situation applies to a character table in the GAP Character Table Library; here we assume that for the library table of a group with the structure \(M.G.A\), the class fusions from \(M.G\) and to \(G.A\) are stored.
gap> FindExtraordinaryCase:= function( tblMGA ) > local result, der, nsg, tblMGAclasses, orders, tblMG, > tblMGfustblMGA, tblMGclasses, pos, M, Mimg, tblMGAfustblGA, tblGA, > outer, inv, filt, other, primes, p; > result:= []; > der:= ClassPositionsOfDerivedSubgroup( tblMGA ); > nsg:= ClassPositionsOfNormalSubgroups( tblMGA ); > tblMGAclasses:= SizesConjugacyClasses( tblMGA ); > orders:= OrdersClassRepresentatives( tblMGA ); > if Length( der ) < NrConjugacyClasses( tblMGA ) then > # Look for tables of normal subgroups of the form $M.G$. > for tblMG in Filtered( List( NamesOfFusionSources( tblMGA ), > CharacterTable ), x -> x <> fail ) do > tblMGfustblMGA:= GetFusionMap( tblMG, tblMGA ); > tblMGclasses:= SizesConjugacyClasses( tblMG ); > pos:= Position( nsg, Set( tblMGfustblMGA ) ); > if pos <> fail and > Size( tblMG ) = Sum( tblMGAclasses{ nsg[ pos ] } ) then > # Look for normal subgroups of the form $M$. > for M in Difference( ClassPositionsOfNormalSubgroups( tblMG ), > [ [ 1 ], [ 1 .. NrConjugacyClasses( tblMG ) ] ] ) do > Mimg:= Set( tblMGfustblMGA{ M } ); > if Sum( tblMGAclasses{ Mimg } ) = Sum( tblMGclasses{ M } ) then > tblMGAfustblGA:= First( ComputedClassFusions( tblMGA ), > r -> ClassPositionsOfKernel( r.map ) = Mimg ); > if tblMGAfustblGA <> fail then > tblGA:= CharacterTable( tblMGAfustblGA.name ); > tblMGAfustblGA:= tblMGAfustblGA.map; > outer:= Difference( [ 1 .. NrConjugacyClasses( tblGA ) ], > CompositionMaps( tblMGAfustblGA, tblMGfustblMGA ) ); > inv:= InverseMap( tblMGAfustblGA ){ outer }; > filt:= Flat( Filtered( inv, IsList ) ); > if not IsEmpty( filt ) then > other:= Filtered( inv, IsInt ); > primes:= Filtered( PrimeDivisors( Size( tblMGA ) ), > p -> ForAll( orders{ filt }, x -> x mod p = 0 ) > and ForAny( orders{ other }, x -> x mod p <> 0 ) ); > for p in primes do > Add( result, [ Identifier( tblMG ), > Identifier( tblMGA ), > Identifier( tblGA ), p ] ); > od; > fi; > fi; > fi; > od; > fi; > od; > fi; > return result; > end;;
Let us list the tables which are found by this function.
gap> cases:= [];; gap> for name in AllCharacterTableNames( IsDuplicateTable, false ) do > Append( cases, FindExtraordinaryCase( CharacterTable( name ) ) ); > od; gap> for i in Set( cases ) do > Print( i, "\n" ); > od; [ "2.A6", "2.A6.2_1", "A6.2_1", 3 ] [ "2.Fi22", "2.Fi22.2", "Fi22.2", 3 ] [ "2.L2(25)", "2.L2(25).2_2", "L2(25).2_2", 5 ] [ "2.L2(49)", "2.L2(49).2_2", "L2(49).2_2", 7 ] [ "2.L2(81)", "2.L2(81).2_1", "L2(81).2_1", 3 ] [ "2.L2(81)", "2.L2(81).4_1", "L2(81).4_1", 3 ] [ "2.L2(81).2_1", "2.L2(81).4_1", "L2(81).4_1", 3 ] [ "2.L4(3)", "2.L4(3).2_2", "L4(3).2_2", 3 ] [ "2.L4(3)", "2.L4(3).2_3", "L4(3).2_3", 3 ] [ "2.S3", "2.D12", "S3x2", 3 ] [ "2.U4(3).2_1", "2.U4(3).(2^2)_{12*2*}", "U4(3).(2^2)_{122}", 3 ] [ "2.U4(3).2_1", "2.U4(3).(2^2)_{122}", "U4(3).(2^2)_{122}", 3 ] [ "2.U4(3).2_1", "2.U4(3).(2^2)_{13*3*}", "U4(3).(2^2)_{133}", 3 ] [ "2.U4(3).2_1", "2.U4(3).(2^2)_{133}", "U4(3).(2^2)_{133}", 3 ] [ "3.U3(8)", "3.U3(8).3_1", "U3(8).3_1", 2 ] [ "3.U3(8)", "3.U3(8).6", "U3(8).6", 2 ] [ "3.U3(8)", "3.U3(8).6", "U3(8).6", 3 ] [ "3.U3(8).2", "3.U3(8).6", "U3(8).6", 2 ] [ "3^2:8", "2.A8N3", "s3wrs2", 3 ] [ "5^(1+2):8:4", "2.HS.2N5", "HS.2N5", 5 ] [ "6.A6", "6.A6.2_1", "3.A6.2_1", 3 ] [ "6.A6", "6.A6.2_1", "A6.2_1", 3 ] [ "6.Fi22", "6.Fi22.2", "3.Fi22.2", 3 ] [ "6.Fi22", "6.Fi22.2", "Fi22.2", 3 ] [ "Isoclinic(2.U4(3).2_1)", "2.U4(3).(2^2)_{1*2*2}", "U4(3).(2^2)_{122}", 3 ] [ "Isoclinic(2.U4(3).2_1)", "2.U4(3).(2^2)_{1*3*3}", "U4(3).(2^2)_{133}", 3 ] [ "bd10", "2.D20", "D20", 5 ]
The smallest example in this list is \(2.A_6.2_1\), the double cover of the symmetric group on six points. The \(3\)-modular table of this group looks as follows.
gap> Display( CharacterTable( "2.A6.2_1" ) mod 3 ); 2.A6.2_1mod3 2 5 5 4 3 1 1 4 4 3 3 2 2 . . . . 1 1 . 5 1 1 . . 1 1 . . . 1a 2a 4a 8a 5a 10a 2b 4b 8b 2P 1a 1a 2a 4a 5a 5a 1a 2a 4a 3P 1a 2a 4a 8a 5a 10a 2b 4b 8b 5P 1a 2a 4a 8a 1a 2a 2b 4b 8b X.1 1 1 1 1 1 1 1 1 1 X.2 1 1 1 1 1 1 -1 -1 -1 X.3 6 6 -2 2 1 1 . . . X.4 4 4 . -2 -1 -1 2 -2 . X.5 4 4 . -2 -1 -1 -2 2 . X.6 9 9 1 1 -1 -1 3 3 -1 X.7 9 9 1 1 -1 -1 -3 -3 1 X.8 4 -4 . . -1 1 . . . X.9 12 -12 . . 2 -2 . . .
We see that the two faithful irreducible characters vanish on the three classes outside \(2.A_6\).
For the groups in the above list, the function BrauerTableOfTypeMGA (CTblLib: BrauerTableOfTypeMGA) can be used to construct the \(p\)-modular tables of \(M.G.A\) from the tables of \(M.G\) and \(G.A\), for the given special primes \(p\). The computations can be performed as follows.
gap> for input in cases do > p:= input[4]; > modtblMG:= CharacterTable( input[1] ) mod p; > ordtblMGA:= CharacterTable( input[2] ); > modtblGA:= CharacterTable( input[3] ) mod p; > name:= Concatenation( Identifier( ordtblMGA ), " mod ", String(p) ); > if ForAll( [ modtblMG, modtblGA ], IsCharacterTable ) then > poss:= BrauerTableOfTypeMGA( modtblMG, modtblGA, ordtblMGA ); > modlib:= ordtblMGA mod p; > if IsCharacterTable( modlib ) then > trans:= TransformingPermutationsCharacterTables( poss.table, > modlib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " differ\n" ); > fi; > else > Print( "#I no library table for ", name, "\n" ); > fi; > else > Print( "#I not all input tables for ", name, " available\n" ); > fi; > od; #I not all input tables for 2.L2(49).2_2 mod 7 available #I not all input tables for 2.L2(81).2_1 mod 3 available #I not all input tables for 2.L2(81).4_1 mod 3 available #I not all input tables for 2.L2(81).4_1 mod 3 available
The examples \(2.A_6.2_1\), \(2.L_2(25).2_2\), and \(2.L_2(49).2_2\) belong to the infinite series of semiliniear groups \(\Sigma\)L\((2,p^2)\), for odd primes \(p\). All groups in this series have the property that all faithful irreducible characters vanish on the \(p\)-regular classes outside SL\((2,p^2)\). (Cf. Section 2.2-6 for another property of the groups in this series.)
The symmetric group \(S_4\) on four points has the form \(G.S_3\) where \(G\) is the Klein four group \(V_4\), \(G.2\) is the dihedral group \(D_8\) of order \(8\), and \(G.3\) is the alternating group \(A_4\). The trivial character of \(A_4\) extends twofold to \(S_4\), in the same way as the trivial character of \(V_4\) extends to the dihedral group. The nontrivial linear characters of \(A_4\) induce irreducibly to \(S_4\). The irreducible degree three character of \(A_4\) is induced from any of the three nontrivial linear characters of \(V_4\), it extends to \(S_4\) in the same way as the unique constituent of the restriction to \(V_4\) that is invariant in the chosen \(D_8\) extends to \(D_8\).
gap> c2:= CharacterTable( "Cyclic", 2 );; gap> t:= c2 * c2;; gap> tC:= CharacterTable( "Dihedral", 8 );; gap> tK:= CharacterTable( "Alternating", 4 );; gap> tfustC:= PossibleClassFusions( t, tC ); [ [ 1, 3, 4, 4 ], [ 1, 3, 5, 5 ], [ 1, 4, 3, 4 ], [ 1, 4, 4, 3 ], [ 1, 5, 3, 5 ], [ 1, 5, 5, 3 ] ] gap> StoreFusion( t, tfustC[1], tC ); gap> tfustK:= PossibleClassFusions( t, tK ); [ [ 1, 2, 2, 2 ] ] gap> StoreFusion( t, tfustK[1], tK ); gap> elms:= PossibleActionsForTypeGS3( t, tC, tK ); [ (3,4) ] gap> new:= CharacterTableOfTypeGS3( t, tC, tK, elms[1], "S4" ); rec( table := CharacterTable( "S4" ), tblCfustblKC := [ 1, 4, 2, 2, 5 ], tblKfustblKC := [ 1, 2, 3, 3 ] ) gap> Display( new.table ); S4 2 3 3 . 2 2 3 1 . 1 . . 1a 2a 3a 4a 2b 2P 1a 1a 3a 2a 1a 3P 1a 2a 1a 4a 2b X.1 1 1 1 1 1 X.2 1 1 1 -1 -1 X.3 3 -1 . 1 -1 X.4 3 -1 . -1 1 X.5 2 2 -1 . .
The case \(e > 1\) occurs in the following example. We choose \(G\) the cyclic group of order two, \(G.C\) the cyclic group of order six, \(G.K\) the quaternion group of order eight, and construct the character table of \(G.F = SL_2(3)\), with \(F \cong A_4\).
We get three extensions of the trivial character of \(G.K\) to \(G.F\), a degree three character induced from the nontrivial linear characters of \(G.K\), and three extensions of the irreducible degree \(2\) character of \(G.K\).
gap> t:= CharacterTable( "Cyclic", 2 );; gap> tC:= CharacterTable( "Cyclic", 6 );; gap> tK:= CharacterTable( "Quaternionic", 8 );; gap> tfustC:= PossibleClassFusions( t, tC ); [ [ 1, 4 ] ] gap> StoreFusion( t, tfustC[1], tC ); gap> tfustK:= PossibleClassFusions( t, tK ); [ [ 1, 3 ] ] gap> StoreFusion( t, tfustK[1], tK ); gap> elms:= PossibleActionsForTypeGS3( t, tC, tK ); [ (2,5,4) ] gap> new:= CharacterTableOfTypeGS3( t, tC, tK, elms[1], "SL(2,3)" ); rec( table := CharacterTable( "SL(2,3)" ), tblCfustblKC := [ 1, 4, 5, 3, 6, 7 ], tblKfustblKC := [ 1, 2, 3, 2, 2 ] ) gap> Display( new.table ); SL(2,3) 2 3 2 3 1 1 1 1 3 1 . 1 1 1 1 1 1a 4a 2a 6a 3a 3b 6b 2P 1a 2a 1a 3a 3b 3a 3b 3P 1a 4a 2a 2a 1a 1a 2a X.1 1 1 1 1 1 1 1 X.2 1 1 1 A /A A /A X.3 1 1 1 /A A /A A X.4 3 -1 3 . . . . X.5 2 . -2 /A -A -/A A X.6 2 . -2 1 -1 -1 1 X.7 2 . -2 A -/A -A /A A = E(3) = (-1+Sqrt(-3))/2 = b3
We demonstrate the construction of all those ordinary and modular character tables in the GAP Character Table Library that are of the type \(G.S_3\) where \(G\) is a simple group or a central extension of a simple group whose character table is contained in the Atlas. Here is the list of Identifier (Reference: Identifier for tables of marks) values needed for accessing the input tables and the known library tables corresponding to the output.
gap> listGS3:= [ > [ "U3(5)", "U3(5).2", "U3(5).3", "U3(5).S3" ], > [ "3.U3(5)", "3.U3(5).2", "3.U3(5).3", "3.U3(5).S3" ], > [ "L3(4)", "L3(4).2_2", "L3(4).3", "L3(4).3.2_2" ], > [ "L3(4)", "L3(4).2_3", "L3(4).3", "L3(4).3.2_3" ], > [ "3.L3(4)", "3.L3(4).2_2", "3.L3(4).3", "3.L3(4).3.2_2" ], > [ "3.L3(4)", "3.L3(4).2_3", "3.L3(4).3", "3.L3(4).3.2_3" ], > [ "2^2.L3(4)", "2^2.L3(4).2_2","2^2.L3(4).3", "2^2.L3(4).3.2_2" ], > [ "2^2.L3(4)", "2^2.L3(4).2_3","2^2.L3(4).3", "2^2.L3(4).3.2_3" ], > [ "U6(2)", "U6(2).2", "U6(2).3", "U6(2).3.2" ], > [ "3.U6(2)", "3.U6(2).2", "3.U6(2).3", "3.U6(2).3.2" ], > [ "2^2.U6(2)", "2^2.U6(2).2", "2^2.U6(2).3", "2^2.U6(2).3.2" ], > [ "O8+(2)", "O8+(2).2", "O8+(2).3", "O8+(2).3.2" ], > [ "2^2.O8+(2)", "2^2.O8+(2).2", "2^2.O8+(2).3", "2^2.O8+(2).3.2" ], > [ "L3(7)", "L3(7).2", "L3(7).3", "L3(7).S3" ], > [ "3.L3(7)", "3.L3(7).2", "3.L3(7).3", "3.L3(7).S3" ], > [ "U3(8)", "U3(8).2", "U3(8).3_2", "U3(8).S3" ], > [ "3.U3(8)", "3.U3(8).2", "3.U3(8).3_2", "3.U3(8).S3" ], > [ "U3(11)", "U3(11).2", "U3(11).3", "U3(11).S3" ], > [ "3.U3(11)", "3.U3(11).2", "3.U3(11).3", "3.U3(11).S3" ], > [ "O8+(3)", "O8+(3).2_2", "O8+(3).3", "O8+(3).S3" ], > [ "2E6(2)", "2E6(2).2", "2E6(2).3", "2E6(2).S3" ], > [ "2^2.2E6(2)", "2^2.2E6(2).2", "2^2.2E6(2).3", "2^2.2E6(2).S3" ], > ];;
(For \(G\) one of \(L_3(4)\), \(U_6(2)\), \(O_8^+(2)\), and \({}^2E_6(2)\), the tables of \(2^2.G\), \(2^2.G.2\), and \(2^2.G.3\) can be constructed with the methods described in Section 2.3-4 and Section 2.3-1, respectively.)
Analogously, the automorphism groups of \(L_3(4)\), \(U_3(8)\), and \(O_8^+(3)\) have factor groups isomorphic with \(S_3\); in these cases, we choose \(G = L_3(4).2_1\), \(G = U_3(8).3_1\), and \(G = O_8^+(3).2^2_{111}\), respectively.
gap> Append( listGS3, [ > [ "L3(4).2_1", "L3(4).2^2", "L3(4).6", "L3(4).D12" ], > [ "2^2.L3(4).2_1", "2^2.L3(4).2^2", "2^2.L3(4).6", "2^2.L3(4).D12" ], > [ "U3(8).3_1", "U3(8).6", "U3(8).3^2", "U3(8).(S3x3)" ], > [ "O8+(3).(2^2)_{111}", "O8+(3).D8", "O8+(3).A4", "O8+(3).S4" ], > ] );
In all these cases, the required table automorphism of \(G.3\) is uniquely determined. We first compute the ordinary character table of \(G.S_3\) and then the \(p\)-modular tables, for all prime divisors \(p\) of the order of \(G\) such that the GAP Character Table Library contains the necessary \(p\)-modular input tables.
In each case, we compare the computed character tables with the ones in the GAP Character Table Library. Note that in order to avoid conflicts of the class fusions that arise in the construction with the class fusions that are already stored on the library tables, we choose identifiers for the result tables that are different from the identifiers of the library tables.
gap> ProcessGS3Example:= function( t, tC, tK, identifier, pi ) > local tF, lib, trans, p, tmodp, tCmodp, tKmodp, modtF; > > tF:= CharacterTableOfTypeGS3( t, tC, tK, pi, > Concatenation( identifier, "new" ) ); > lib:= CharacterTable( identifier ); > if lib <> fail then > trans:= TransformingPermutationsCharacterTables( tF.table, lib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for `", identifier, > "' differ\n" ); > fi; > else > Print( "#I no library table for `", identifier, "'\n" ); > fi; > StoreFusion( tC, tF.tblCfustblKC, tF.table ); > StoreFusion( tK, tF.tblKfustblKC, tF.table ); > for p in PrimeDivisors( Size( t ) ) do > tmodp := t mod p; > tCmodp:= tC mod p; > tKmodp:= tK mod p; > if IsCharacterTable( tmodp ) and > IsCharacterTable( tCmodp ) and > IsCharacterTable( tKmodp ) then > modtF:= CharacterTableOfTypeGS3( tmodp, tCmodp, tKmodp, > tF.table, > Concatenation( identifier, "mod", String( p ) ) ); > if Length( Irr( modtF.table ) ) <> > Length( Irr( modtF.table )[1] ) then > Print( "#E nonsquare result table for `", > identifier, " mod ", p, "'\n" ); > elif lib <> fail and IsCharacterTable( lib mod p ) then > trans:= TransformingPermutationsCharacterTables( modtF.table, > lib mod p ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for `", > identifier, " mod ", p, "' differ\n" ); > fi; > else > Print( "#I no library table for `", identifier, " mod ", > p, "'\n" ); > fi; > else > Print( "#I not all inputs available for `", identifier, > " mod ", p, "'\n" ); > fi; > od; > end;;
Now we call the function for the examples in the list.
gap> for input in listGS3 do > t := CharacterTable( input[1] ); > tC:= CharacterTable( input[2] ); > tK:= CharacterTable( input[3] ); > identifier:= input[4]; > elms:= PossibleActionsForTypeGS3( t, tC, tK ); > if Length( elms ) = 1 then > ProcessGS3Example( t, tC, tK, identifier, elms[1] ); > else > Print( "#I ", Length( elms ), " actions possible for `", > identifier, "'\n" ); > fi; > od; #I not all inputs available for `O8+(3).S3 mod 3' #I not all inputs available for `2E6(2).S3 mod 2' #I not all inputs available for `2E6(2).S3 mod 3' #I not all inputs available for `2E6(2).S3 mod 5' #I not all inputs available for `2E6(2).S3 mod 7' #I not all inputs available for `2E6(2).S3 mod 11' #I not all inputs available for `2E6(2).S3 mod 13' #I not all inputs available for `2E6(2).S3 mod 17' #I not all inputs available for `2E6(2).S3 mod 19' #I not all inputs available for `2^2.2E6(2).S3 mod 2' #I not all inputs available for `2^2.2E6(2).S3 mod 3' #I not all inputs available for `2^2.2E6(2).S3 mod 5' #I not all inputs available for `2^2.2E6(2).S3 mod 7' #I not all inputs available for `2^2.2E6(2).S3 mod 11' #I not all inputs available for `2^2.2E6(2).S3 mod 13' #I not all inputs available for `2^2.2E6(2).S3 mod 17' #I not all inputs available for `2^2.2E6(2).S3 mod 19' #I not all inputs available for `U3(8).(S3x3) mod 2' #I not all inputs available for `U3(8).(S3x3) mod 19' #I not all inputs available for `O8+(3).S4 mod 3'
Also the ordinary character table of the automorphic extension of the simple Atlas group \(O_8^+(3)\) by \(A_4\) can be constructed with the same approach. Here we get four possible permutations, which lead to essentially the same character table.
gap> input:= [ "O8+(3)", "O8+(3).3", "O8+(3).(2^2)_{111}", "O8+(3).A4" ];; gap> t := CharacterTable( input[1] );; gap> tC:= CharacterTable( input[2] );; gap> tK:= CharacterTable( input[3] );; gap> identifier:= input[4];; gap> elms:= PossibleActionsForTypeGS3( t, tC, tK );; gap> Length( elms ); 4 gap> differ:= MovedPoints( Group( List( elms, x -> x / elms[1] ) ) );; gap> List( elms, x -> RestrictedPerm( x, differ ) ); [ (118,216,169)(119,217,170)(120,218,167)(121,219,168), (118,216,170)(119,217,169)(120,219,168)(121,218,167), (118,217,169)(119,216,170)(120,218,168)(121,219,167), (118,217,170)(119,216,169)(120,219,167)(121,218,168) ] gap> poss:= List( elms, pi -> CharacterTableOfTypeGS3( t, tC, tK, pi, > Concatenation( identifier, "new" ) ) );; gap> lib:= CharacterTable( identifier );; gap> ForAll( poss, r -> IsRecord( > TransformingPermutationsCharacterTables( r.table, lib ) ) ); true
Also the construction of the \(p\)-modular tables of \(O_8^+(3).A_4\) works.
gap> ProcessGS3Example( t, tC, tK, identifier, elms[1] ); #I not all inputs available for `O8+(3).A4 mod 3'
As the first example, we consider the automorphism group Aut\(( A_6 ) \cong A_6.2^2\) of the alternating group \(A_6\) on six points.
In this case, the triple of actions on the subgroups \(A_6.2_i\) is uniquely determined by the condition on the number of conjugacy classes in Section 2.3-3.
gap> tblG:= CharacterTable( "A6" );; gap> tblsG2:= List( [ "A6.2_1", "A6.2_2", "A6.2_3" ], CharacterTable );; gap> List( tblsG2, NrConjugacyClasses ); [ 11, 11, 8 ] gap> possact:= List( tblsG2, x -> Filtered( Elements( > AutomorphismsOfTable( x ) ), y -> Order( y ) <= 2 ) ); [ [ (), (3,4)(7,8)(10,11) ], [ (), (8,9), (5,6)(10,11), (5,6)(8,9)(10,11) ], [ (), (7,8) ] ]
Note that \(n_1 = n_2\) implies \(f_1 = f_2\), and \(n_1 - n_3 = 3\) implies \(f_1 - f_3 = 2\), so we get \(f_1 = 3\) and \(f_3 = 1\), and \(A_6.2^2\) has \(2 \cdot 11 - 3 \cdot 3 = 2 \cdot 8 - 3 \cdot 1 = 13\) classes.
(The compatibility on the classes inside \(A_6\) yields only that the classes \(3\) and \(4\) of \(A_6.2_1 \cong S_6\) must be fused in \(A_6.2^2\), as well as the classes \(5\) and \(6\) of \(A_6.2_2 \cong\) PGL\((2,9)\).)
gap> List( tblsG2, x -> GetFusionMap( tblG, x ) ); [ [ 1, 2, 3, 4, 5, 6, 6 ], [ 1, 2, 3, 3, 4, 5, 6 ], [ 1, 2, 3, 3, 4, 5, 5 ] ]
These arguments are used by the GAP function PossibleActionsForTypeGV4 (CTblLib: PossibleActionsForTypeGV4), which returns the list of all possible triples of permutations such that the \(i\)-th permutation describes the action of \(A_6.2^2\) on the classes of \(A_6.2_i\).
gap> acts:= PossibleActionsForTypeGV4( tblG, tblsG2 ); [ [ (3,4)(7,8)(10,11), (5,6)(8,9)(10,11), (7,8) ] ]
For the given actions, the GAP function PossibleCharacterTablesOfTypeGV4 (CTblLib: PossibleCharacterTablesOfTypeGV4) then computes the possibilities for the character table of \(A_6.2^2\); in this case, the result is unique.
gap> poss:= PossibleCharacterTablesOfTypeGV4( tblG, tblsG2, acts[1], > "A6.2^2" ); [ rec( G2fusGV4 := [ [ 1, 2, 3, 3, 4, 5, 6, 6, 7, 8, 8 ], [ 1, 2, 3, 4, 5, 5, 9, 10, 10, 11, 11 ], [ 1, 2, 3, 4, 5, 12, 13, 13 ] ], table := CharacterTable( "A6.2^2" ) ) ] gap> IsRecord( TransformingPermutationsCharacterTables( poss[1].table, > CharacterTable( "A6.2^2" ) ) ); true
Finally, possible \(p\)-modular tables can be computed from the \(p\)-modular input tables and the ordinary table of \(A_6.2^2\); here we show this for \(p = 3\).
gap> PossibleCharacterTablesOfTypeGV4( tblG mod 3, > List( tblsG2, t -> t mod 3 ), poss[1].table ); [ rec( G2fusGV4 := [ [ 1, 2, 3, 4, 5, 5, 6 ], [ 1, 2, 3, 4, 4, 7, 8, 8, 9, 9 ], [ 1, 2, 3, 4, 10, 11, 11 ] ], table := BrauerTable( "A6.2^2", 3 ) ) ]
We demonstrate the construction of all those ordinary and modular character tables in the GAP Character Table Library that are of the type \(G.2^2\) where \(G\) is a simple group or a central extension of a simple group whose character table is contained in the Atlas. Here is the list of Identifier (Reference: Identifier for tables of marks) values needed for accessing the input tables and the result tables.
(The construction of the character table of \(O_8^+(3).2^2_{111}\) is more involved and will be described in Section 2.6-10. The construction of the character tables of groups of the type \(2.L_3(4).2^2\) and \(6.L_3(4).2^2\) is described in the sections 2.6-4 and 2.6-5, respectively. The construction of the character tables of groups of the type \(2.U_4(3).2^2\) is described in Section 2.6-6.)
gap> listGV4:= [ > [ "A6", "A6.2_1", "A6.2_2", "A6.2_3", "A6.2^2" ], > [ "3.A6", "3.A6.2_1", "3.A6.2_2", "3.A6.2_3", "3.A6.2^2" ], > [ "L2(25)", "L2(25).2_1", "L2(25).2_2", "L2(25).2_3", "L2(25).2^2" ], > [ "L3(4)", "L3(4).2_1", "L3(4).2_2", "L3(4).2_3", "L3(4).2^2" ], > [ "2^2.L3(4)", "2^2.L3(4).2_1", "2^2.L3(4).2_2", "2^2.L3(4).2_3", > "2^2.L3(4).2^2" ], > [ "3.L3(4)", "3.L3(4).2_1", "3.L3(4).2_2", "3.L3(4).2_3", "3.L3(4).2^2" ], > [ "U4(3)", "U4(3).2_1", "U4(3).2_2", "U4(3).2_2'", > "U4(3).(2^2)_{122}" ], > [ "U4(3)", "U4(3).2_1", "U4(3).2_3", "U4(3).2_3'", > "U4(3).(2^2)_{133}" ], > [ "3_1.U4(3)", "3_1.U4(3).2_1", "3_1.U4(3).2_2", "3_1.U4(3).2_2'", > "3_1.U4(3).(2^2)_{122}" ], > [ "3_2.U4(3)", "3_2.U4(3).2_1", "3_2.U4(3).2_3", "3_2.U4(3).2_3'", > "3_2.U4(3).(2^2)_{133}" ], > [ "L2(49)", "L2(49).2_1", "L2(49).2_2", "L2(49).2_3", "L2(49).2^2" ], > [ "L2(81)", "L2(81).2_1", "L2(81).2_2", "L2(81).2_3", "L2(81).2^2" ], > [ "L3(9)", "L3(9).2_1", "L3(9).2_2", "L3(9).2_3", "L3(9).2^2" ], > [ "O8+(3)", "O8+(3).2_1", "O8+(3).2_2", "O8+(3).2_2'", > "O8+(3).(2^2)_{122}" ], > [ "O8-(3)", "O8-(3).2_1", "O8-(3).2_2", "O8-(3).2_3", "O8-(3).2^2" ], > ];;
Analogously, the automorphism groups \(L_3(4).D_{12}\) of \(L_3(4)\) and \(U_4(3).D_8\) of \(U_4(3)\), and the subgroup \(O_8^+(3).D_8\) of the automorphism group \(O_8^+(3).S_4\) have factor groups that are isomorphic with \(2^2\); in these cases, we choose \(G = L_3(4).3\), \(G = U_4(3).2_1\), and \(G = O_8^+(3).2_1\), respectively.
Also the group \(2^2.L_3(4).D_{12}\) has a factor group isomorphic with \(2^2\). Note that the character tables of \(L_3(4).D_{12}\) and \(2^2.L_3(4).D_{12}\) have been constructed already in Section 2.5-2.
The automorphism groups of \(L_4(4)\) and \(U_4(5)\) have the structure \(L_4(4).2^2\) and \(U_4(5).2^2\), respectively; their tables are contained in the GAP Character Table Library but not in the Atlas.
gap> Append( listGV4, [ > [ "L3(4).3", "L3(4).6", "L3(4).3.2_2", "L3(4).3.2_3", "L3(4).D12" ], > [ "2^2.L3(4).3", "2^2.L3(4).6", "2^2.L3(4).3.2_2", "2^2.L3(4).3.2_3", > "2^2.L3(4).D12" ], > [ "U4(3).2_1", "U4(3).4", "U4(3).(2^2)_{122}", "U4(3).(2^2)_{133}", > "U4(3).D8" ], > [ "O8+(3).2_1", "O8+(3).(2^2)_{111}", "O8+(3).(2^2)_{122}", "O8+(3).4", > "O8+(3).D8" ], > [ "L4(4)", "L4(4).2_1", "L4(4).2_2", "L4(4).2_3", "L4(4).2^2" ], > [ "U4(5)", "U4(5).2_1", "U4(5).2_2", "U4(5).2_3", "U4(5).2^2" ], > ] );
Now we proceed in two steps, the computation of the possible ordinary character tables from the ordinary tables of the relevant subgroups, and then the computation of the Brauer tables from the Brauer tables of the relevant subgroups and from the ordinary table of the group.
The following function first computes the possible triples of actions on the subgroups \(G.2_i\), using the function PossibleActionsForTypeGV4 (CTblLib: PossibleActionsForTypeGV4). Then the union of the candidate tables for these actions is computed, this list is returned in the end. and representatives of classes of permutation equivalent candidates are inspected further with consistency checks. If there is a unique solution up to permutation equivalence, this table is compared with the one that is contained in the GAP Character Table Library.
gap> ConstructOrdinaryGV4Table:= function( tblG, tblsG2, name, lib ) > local acts, nam, poss, reps, i, trans; > > # Compute the possible actions for the ordinary tables. > acts:= PossibleActionsForTypeGV4( tblG, tblsG2 ); > # Compute the possible ordinary tables for the given actions. > nam:= Concatenation( "new", name ); > poss:= Concatenation( List( acts, triple -> > PossibleCharacterTablesOfTypeGV4( tblG, tblsG2, triple, nam ) ) ); > # Test the possibilities for permutation equivalence. > reps:= RepresentativesCharacterTables( poss ); > if 1 < Length( reps ) then > Print( "#I ", name, ": ", Length( reps ), > " equivalence classes\n" ); > elif Length( reps ) = 0 then > Print( "#E ", name, ": no solution\n" ); > else > # Compare the computed table with the library table. > if not IsCharacterTable( lib ) then > Print( "#I no library table for ", name, "\n" ); > PrintToLib( name, poss[1].table ); > for i in [ 1 .. 3 ] do > Print( LibraryFusion( tblsG2[i], > rec( name:= name, map:= poss[1].G2fusGV4[i] ) ) ); > od; > else > trans:= TransformingPermutationsCharacterTables( poss[1].table, > lib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " differ\n" ); > fi; > # Compare the computed fusions with the stored ones. > if List( poss[1].G2fusGV4, x -> OnTuples( x, trans.columns ) ) > <> List( tblsG2, x -> GetFusionMap( x, lib ) ) then > Print( "#E computed and stored fusions for ", name, > " differ\n" ); > fi; > fi; > fi; > return poss; > end;;
The following function computes, for all those prime divisors \(p\) of the group order in question such that the \(p\)-modular Brauer tables of the subgroups \(G.2_i\) are available, the possible \(p\)-modular Brauer tables. If the solution is unique up to permutation equivalence, it is compared with the table that is contained in the GAP Character Table Library.
It may happen (even in the case that the ordinary character table is unique up to permutation equivalence) that some candidates for the ordinary character table are excluded due to information provided by some \(p\)-modular table. In this case, a message is printed, and the ordinary character table from the GAP Character Table Library is checked again under the additional restrictions.
gap> ConstructModularGV4Tables:= function( tblG, tblsG2, ordposs, > ordlibtblGV4 ) > local name, modposs, primes, checkordinary, i, record, p, tmodp, > t2modp, poss, modlib, trans, reps; > > if not IsCharacterTable( ordlibtblGV4 ) then > Print( "#I no ordinary library table ...\n" ); > return []; > fi; > name:= Identifier( ordlibtblGV4 ); > modposs:= List( ordposs, x -> [] ); > primes:= ShallowCopy( PrimeDivisors( Size( tblG ) ) ); > ordposs:= ShallowCopy( ordposs ); > checkordinary:= false; > for i in [ 1 .. Length( ordposs ) ] do > record:= ordposs[i]; > for p in primes do > tmodp := tblG mod p; > t2modp:= List( tblsG2, t2 -> t2 mod p ); > if IsCharacterTable( tmodp ) and > ForAll( t2modp, IsCharacterTable ) then > poss:= PossibleCharacterTablesOfTypeGV4( tmodp, t2modp, > record.table, record.G2fusGV4 ); > poss:= RepresentativesCharacterTables( poss ); > if Length( poss ) = 0 then > Print( "#I excluded cand. ", i, " (out of ", > Length( ordposs ), ") for ", name, " by ", p, > "-mod. table\n" ); > Unbind( ordposs[i] ); > Unbind( modposs[i] ); > checkordinary:= true; > break; > elif Length( poss ) = 1 then > # Compare the computed table with the library table. > modlib:= ordlibtblGV4 mod p; > if IsCharacterTable( modlib ) then > trans:= TransformingPermutationsCharacterTables( > poss[1].table, modlib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", > name, " mod ", p, " differ\n" ); > fi; > else > Print( "#I no library table for ", > name, " mod ", p, "\n" ); > PrintToLib( name, poss[1].table ); > fi; > else > Print( "#I ", name, " mod ", p, ": ", Length( poss ), > " equivalence classes\n" ); > fi; > Add( modposs[i], poss ); > elif i = 1 then > Print( "#I not all input tables for ", name, " mod ", p, > " available\n" ); > primes:= Difference( primes, [ p ] ); > fi; > od; > od; > if checkordinary then > # Test whether the ordinary table is admissible. > ordposs:= Compacted( ordposs ); > modposs:= Compacted( modposs ); > reps:= RepresentativesCharacterTables( ordposs ); > if 1 < Length( reps ) then > Print( "#I ", name, ": ", Length( reps ), > " equivalence classes (ord. table)\n" ); > elif Length( reps ) = 0 then > Print( "#E ", name, ": no solution (ord. table)\n" ); > else > # Compare the computed table with the library table. > trans:= TransformingPermutationsCharacterTables( > ordposs[1].table, ordlibtblGV4 ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " differ\n" ); > fi; > # Compare the computed fusions with the stored ones. > if List( ordposs[1].G2fusGV4, x -> OnTuples( x, trans.columns ) ) > <> List( tblsG2, x -> GetFusionMap( x, ordlibtblGV4 ) ) then > Print( "#E computed and stored fusions for ", name, > " differ\n" ); > fi; > fi; > fi; > return rec( ordinary:= ordposs, modular:= modposs ); > end;;
Finally, here is the loop over the list of tables.
gap> for input in listGV4 do > tblG := CharacterTable( input[1] ); > tblsG2 := List( input{ [ 2 .. 4 ] }, CharacterTable ); > lib := CharacterTable( input[5] ); > poss := ConstructOrdinaryGV4Table( tblG, tblsG2, input[5], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > od; #I excluded cand. 2 (out of 2) for L3(4).2^2 by 3-mod. table #I excluded cand. 2 (out of 8) for 2^2.L3(4).2^2 by 7-mod. table #I excluded cand. 3 (out of 8) for 2^2.L3(4).2^2 by 5-mod. table #I excluded cand. 4 (out of 8) for 2^2.L3(4).2^2 by 5-mod. table #I excluded cand. 5 (out of 8) for 2^2.L3(4).2^2 by 5-mod. table #I excluded cand. 6 (out of 8) for 2^2.L3(4).2^2 by 5-mod. table #I excluded cand. 7 (out of 8) for 2^2.L3(4).2^2 by 7-mod. table #I excluded cand. 2 (out of 2) for 3.L3(4).2^2 by 3-mod. table #I excluded cand. 2 (out of 2) for L3(9).2^2 by 7-mod. table #I not all input tables for O8+(3).(2^2)_{122} mod 3 available #I not all input tables for O8-(3).2^2 mod 3 available #I not all input tables for O8-(3).2^2 mod 5 available #I not all input tables for O8-(3).2^2 mod 7 available #I not all input tables for O8-(3).2^2 mod 13 available #I not all input tables for O8-(3).2^2 mod 41 available #I excluded cand. 2 (out of 2) for L3(4).D12 by 3-mod. table #I excluded cand. 2 (out of 2) for 2^2.L3(4).D12 by 7-mod. table #I not all input tables for O8+(3).D8 mod 3 available #I not all input tables for L4(4).2^2 mod 3 available #I not all input tables for L4(4).2^2 mod 5 available #I not all input tables for L4(4).2^2 mod 7 available #I not all input tables for L4(4).2^2 mod 17 available #I not all input tables for U4(5).2^2 mod 2 available #I not all input tables for U4(5).2^2 mod 3 available #I not all input tables for U4(5).2^2 mod 5 available #I not all input tables for U4(5).2^2 mod 7 available #I not all input tables for U4(5).2^2 mod 13 available
The groups \(3.A_6.2^2\), \(3.L_3(4).2^2\), and \(3_2.U_4(3).(2^2)_{133}\) have also the structure \(M.G.A\), with \(M.G\) equal to \(3.A_6.2_3\), \(3.L_3(4).2_1\), and \(3_2.U_4(3).2_3\), respectively, and \(G.A\) equal to \(A_6.2^2\), \(L_3(4).2^2\), and \(U_4(3).(2^2)_{133}\), respectively (see Section 2.4-3).
Similarly, the group \(L_3(4).D_{12}\) has also the structure \(G.S_3\), with \(G = L_3(4).2_1\), \(G.2 = L_3(4).2^2\), and \(G.3 = L_3(4).6\), respectively (see Section 2.5-2).
The available functions yield two possibilities for the ordinary character table of \(S_4(9).2^2\).
gap> tblG:= CharacterTable( "S4(9)" );; gap> tblsG2:= List( [ "S4(9).2_1", "S4(9).2_2", "S4(9).2_3" ], > CharacterTable );; gap> lib:= CharacterTable( "S4(9).2^2" );; gap> poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, "newS4(9).2^2", lib );; #I newS4(9).2^2: 2 equivalence classes gap> poss:= RepresentativesCharacterTables( poss );;
The two candidates differ w. r. t. the action of \(S_4(9).2^2\) on the classes of element order \(80\) in \(S_4(9).2_2\). In the two possible tables, each element of order \(80\) is conjugate to its third power or to its \(13\)-th power, respectively.
gap> order80:= PositionsProperty( OrdersClassRepresentatives( tblsG2[2] ), > x -> x = 80 ); [ 98, 99, 100, 101, 102, 103, 104, 105 ] gap> List( poss, r -> r.G2fusGV4[2]{ order80 } ); [ [ 77, 77, 78, 79, 80, 78, 79, 80 ], [ 77, 78, 79, 79, 77, 80, 80, 78 ] ] gap> PowerMap( tblsG2[2], 3 ){ order80 }; [ 99, 98, 103, 104, 105, 100, 101, 102 ] gap> PowerMap( tblsG2[2], 13 ){ order80 }; [ 102, 105, 101, 100, 98, 104, 103, 99 ]
We claim that the first candidate is the correct one. For that, first note that \(S_4(9).2_2\) is the extension of the simple group by a diagonal automorphism. (An easy way to see this is that for any subgroup of \(S_4(9)\) isomorphic with \(S_2(81) \cong L_2(81)\), the extension by a diagonal automorphism contains elements of order \(80\) –this group is isomorphic with PGL\((2,81)\)– and only \(S_4(9).2_2\) contains elements of order \(80\).)
gap> List( tblsG2, x -> 80 in OrdersClassRepresentatives( x ) ); [ false, true, false ]
Now the field automorphism of \(S_4(9).2_2\) maps each element \(x\) of order \(80\) in \(S_4(9).2_2\) to a conjugate of \(x^3\).
gap> tbl:= poss[1].table;; gap> IsRecord( TransformingPermutationsCharacterTables( tbl, lib ) ); true
The outer automorphism group of the group \(L_3(4)\) is a dihedral group of order \(12\); its Sylow \(2\)-subgroups are Klein four groups, so there is a unique almost simple group \(H\) of the type \(L_3(4).2^2\), up to isomorphism. In this section, we construct the character tables of the double covers of this group with the approach from Section 2.3-3.
The group \(H\) has three subgroups of index two, of the types \(L_3(4).2_1\), \(L_3(4).2_2\), and \(L_3(4).2_3\), respectively. So any double cover of \(H\) contains one subgroup of each of the types \(2.L_3(4).2_1\), \(2.L_3(4).2_2\), and \(2.L_3(4).2_3\), and there are two isoclinic variants of each of these group to consider, see Section 2.2-6. So we start with eight different inputs for the construction of the character tables of double covers.
gap> names:= List( [ 1 .. 3 ], > i -> Concatenation( "2.L3(4).2_", String( i ) ) );; gap> tbls:= List( names, CharacterTable ); [ CharacterTable( "2.L3(4).2_1" ), CharacterTable( "2.L3(4).2_2" ), CharacterTable( "2.L3(4).2_3" ) ] gap> isos:= List( names, nam -> CharacterTable( Concatenation( nam, "*" ) ) ); [ CharacterTable( "Isoclinic(2.L3(4).2_1)" ), CharacterTable( "Isoclinic(2.L3(4).2_2)" ), CharacterTable( "Isoclinic(2.L3(4).2_3)" ) ] gap> inputs:= [ > [ tbls[1], tbls[2], tbls[3], "2.L3(4).(2^2)_{123}" ], > [ tbls[1], isos[2], tbls[3], "2.L3(4).(2^2)_{12*3}" ], > [ tbls[1], tbls[2], isos[3], "2.L3(4).(2^2)_{123*}" ], > [ tbls[1], isos[2], isos[3], "2.L3(4).(2^2)_{12*3*}" ], > [ isos[1], tbls[2], tbls[3], "2.L3(4).(2^2)_{1*23}" ], > [ isos[1], isos[2], tbls[3], "2.L3(4).(2^2)_{1*2*3}" ], > [ isos[1], tbls[2], isos[3], "2.L3(4).(2^2)_{1*23*}" ], > [ isos[1], isos[2], isos[3], "2.L3(4).(2^2)_{1*2*3*}" ] ];; gap> tblG:= CharacterTable( "2.L3(4)" );; gap> result:= [];; gap> for input in inputs do > tblsG2:= input{ [ 1 .. 3 ] }; > lib:= CharacterTable( input[4] ); > poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, input[4], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > Append( result, RepresentativesCharacterTables( poss ) ); > od; #I excluded cand. 2 (out of 8) for 2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 3 (out of 8) for 2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 4 (out of 8) for 2.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 5 (out of 8) for 2.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 6 (out of 8) for 2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 7 (out of 8) for 2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 2 (out of 8) for 2.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 3 (out of 8) for 2.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 4 (out of 8) for 2.L3(4).(2^2)_{12*3*} by 7-mod. table #I excluded cand. 5 (out of 8) for 2.L3(4).(2^2)_{12*3*} by 7-mod. table #I excluded cand. 6 (out of 8) for 2.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 7 (out of 8) for 2.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 2 (out of 8) for 2.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 3 (out of 8) for 2.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 4 (out of 8) for 2.L3(4).(2^2)_{1*2*3} by 7-mod. table #I excluded cand. 5 (out of 8) for 2.L3(4).(2^2)_{1*2*3} by 7-mod. table #I excluded cand. 6 (out of 8) for 2.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 7 (out of 8) for 2.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 2 (out of 8) for 2.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 3 (out of 8) for 2.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 4 (out of 8) for 2.L3(4).(2^2)_{1*23*} by 7-mod. table #I excluded cand. 5 (out of 8) for 2.L3(4).(2^2)_{1*23*} by 7-mod. table #I excluded cand. 6 (out of 8) for 2.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 7 (out of 8) for 2.L3(4).(2^2)_{1*23*} by 5-mod. table gap> result:= List( result, x -> x.table ); [ CharacterTable( "new2.L3(4).(2^2)_{123}" ), CharacterTable( "new2.L3(4).(2^2)_{12*3}" ), CharacterTable( "new2.L3(4).(2^2)_{123*}" ), CharacterTable( "new2.L3(4).(2^2)_{12*3*}" ), CharacterTable( "new2.L3(4).(2^2)_{1*23}" ), CharacterTable( "new2.L3(4).(2^2)_{1*2*3}" ), CharacterTable( "new2.L3(4).(2^2)_{1*23*}" ), CharacterTable( "new2.L3(4).(2^2)_{1*2*3*}" ) ]
We get exactly one character table for each input. For each of these tables, there are three possibilities to form an isoclinic table, corresponding to the three subgroups of index two. It turns out that the eight solutions form two orbits under forming some isoclinic table. Tables in different orbits are essentially different, already their numbers of conjugacy classes differ.
gap> List( result, NrConjugacyClasses ); [ 39, 33, 33, 39, 33, 39, 39, 33 ] gap> t:= result[1];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 4, 7, 6 ] gap> t:= result[2];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 3, 8, 5 ]
Up to now, it is not clear that the character tables we have constructed are really the character tables of some groups. The existence of groups for the first orbit of character tables can be established as follows.
The group \(U_6(2).2\) contains a maximal subgroup \(M\) of the type \(L_3(4).2^2\), see [CCN+85, p. 115]. Its derived subgroup \(M'\) of the type \(L_3(4)\) lies inside \(U_6(2)\), and we claim that the preimage of \(M'\) under the natural epimorphism from \(2.U_6(2)\) to \(U_6(2)\) is a double cover of \(L_3(4)\). Unfortunately, \(L_3(4)\) admits class fusions into \(2.U_6(2)\), so this criterion cannot be used.
gap> l34:= CharacterTable( "L3(4)" );; gap> u:= CharacterTable( "U6(2)" );; gap> 2u:= CharacterTable( "2.U6(2)" );; gap> cand:= PossibleClassFusions( l34, 2u ); [ [ 1, 5, 12, 16, 22, 22, 23, 23, 41, 41 ], [ 1, 5, 12, 22, 16, 22, 23, 23, 41, 41 ], [ 1, 5, 12, 22, 22, 16, 23, 23, 41, 41 ] ] gap> OrdersClassRepresentatives( l34 ); [ 1, 2, 3, 4, 4, 4, 5, 5, 7, 7 ]
Consider the three classes of elements of order four in \(L_3(4)\). Under the possible fusions into \(2.U_6(2)\), they are mapped to the classes \(16\) and \(22\), which are preimages of the classes \(10\) and \(14\) (4C and 4G) of \(U_6(2)\). Note that the maximal subgroups of type \(L_3(4).2\) in \(U_6(2)\) extend to \(L_3(4).6\) type subgroups in \(U_6(2).3\), and the three classes 4C, 4D, 4E form one orbit under the action of an outer automorphism of order three of \(U_6(2)\).
gap> GetFusionMap( 2u, u ){ [ 16, 22 ] }; [ 10, 14 ] gap> ClassNames( u, "ATLAS" ){ [ 10, 14 ] }; [ "4C", "4G" ] gap> GetFusionMap( u, CharacterTable( "U6(2).3" ) ); [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 24, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 36, 36, 37, 38, 39, 40 ]
This means that any \(L_3(4)\) type subgroup of \(U_6(2)\) that extends to an \(L_3(4).6\) type subgroup in \(U_6(2).3\) either contains elements from all three classes 4C, 4D, 4E of \(U_6(2)\), or contains no element from these classes. Thus we know that any double cover of \(U_6(2).2\) contains a double cover of \(L_3(4).2^2\). Only the first of our result tables admits a class fusion into the table of \(2.U_6(2).2\).
gap> 2u2:= CharacterTable( "2.U6(2).2" );; gap> fus:= List( result, x -> PossibleClassFusions( x, 2u2 ) );; gap> List( fus, Length ); [ 4, 0, 0, 0, 0, 0, 0, 0 ]
As a consequence, the fourth result table is established as that of a maximal subgroup of the group isoclinic to \(2.U_6(2).2\).
gap> 2u2iso:= CharacterTableIsoclinic( 2u2 );; gap> fus:= List( result, x -> PossibleClassFusions( x, 2u2iso ) );; gap> List( fus, Length ); [ 0, 0, 0, 4, 0, 0, 0, 0 ]
Similarly, the group \(HS.2\) contains a maximal subgroup \(M\) of the type \(L_3(4).2^2\), see [CCN+85, p. 80]. Its derived subgroup \(M'\) of the type \(L_3(4)\) lies inside \(HS\), and the preimage of \(M'\) under the natural epimorphism from \(2.HS\) to \(HS\) is a double cover of \(L_3(4)\), because \(L_3(4)\) does not admit a class fusion into \(2.HS.2\).
gap> h2:= CharacterTable( "HS.2" );; gap> 2h2:= CharacterTable( "2.HS.2" );; gap> PossibleClassFusions( l34, 2h2 ); [ ]
Only the fifth of our result tables admits a class fusion into \(2.HS.2\), which means that \(2.L_3(4).(2^2)_{1{\ast}23}\) is a subgroup of \(2.HS.2\), and the eighth result table –\(2.L_3(4).(2^2)_{1{\ast}2{\ast}3{\ast}}\)– admits a class fusion into the isoclinic variant of \(2.HS.2\) This shows the existence of groups for the tables from the second orbit.
gap> fus:= List( result, x -> PossibleClassFusions( x, 2h2 ) );; gap> List( fus, Length ); [ 0, 0, 0, 0, 4, 0, 0, 0 ] gap> 2h2iso:= CharacterTableIsoclinic( 2h2 );; gap> fus:= List( result, x -> PossibleClassFusions( x, 2h2iso ) );; gap> List( fus, Length ); [ 0, 0, 0, 0, 0, 0, 0, 4 ]
We have two approaches for constructing the character tables of these groups.
First, we may regard them as normal products of the three normal subgroups of index two, each of them having the structure \(6.L_3(4).2\), and use the approach from Section 2.3-3, as we did in Section 2.6-4 for the groups of the structure \(2.L_3(4).2^2\).
Second, we may use the approach from Section 2.3-1. Note that the factor group \(L_3(4).2^2\) contains each of the three groups \(L_3(4).2_i\) as a subgroup, for \(1 \leq i \leq 3\), and the groups of the type \(6.L_3(4).2_1\) have a centre of order six, whereas the centres of the \(6.L_3(4).2_2\) and \(6.L_3(4).2_3\) type groups have order two. For that, the character tables of the subgroups \(6.L_3(4).2_1\) and \(6.L_3(4).2_1^{\ast}\) are needed, as well as the character tables of the eight possible factor groups \(2.L_3(4).2^2\); the latter tables are known from Section 2.6-4.
We show both approaches. (The second approach is better suited for storing the character tables in the Character Table Library, since the irreducible characters need not be stored, and since the Brauer tables of the groups can be derived from the Brauer tables of the compound tables.)
gap> tbls:= List( [ "1", "2", "3" ], > i -> CharacterTable( Concatenation( "6.L3(4).2_", i ) ) ); [ CharacterTable( "6.L3(4).2_1" ), CharacterTable( "6.L3(4).2_2" ), CharacterTable( "6.L3(4).2_3" ) ] gap> isos:= List( [ "1", "2", "3" ], > i -> CharacterTable( Concatenation( "6.L3(4).2_", i, "*" ) ) ); [ CharacterTable( "Isoclinic(6.L3(4).2_1)" ), CharacterTable( "Isoclinic(6.L3(4).2_2)" ), CharacterTable( "Isoclinic(6.L3(4).2_3)" ) ] gap> inputs:= [ > [ tbls[1], tbls[2], tbls[3], "6.L3(4).(2^2)_{123}" ], > [ tbls[1], isos[2], tbls[3], "6.L3(4).(2^2)_{12*3}" ], > [ tbls[1], tbls[2], isos[3], "6.L3(4).(2^2)_{123*}" ], > [ tbls[1], isos[2], isos[3], "6.L3(4).(2^2)_{12*3*}" ], > [ isos[1], tbls[2], tbls[3], "6.L3(4).(2^2)_{1*23}" ], > [ isos[1], isos[2], tbls[3], "6.L3(4).(2^2)_{1*2*3}" ], > [ isos[1], tbls[2], isos[3], "6.L3(4).(2^2)_{1*23*}" ], > [ isos[1], isos[2], isos[3], "6.L3(4).(2^2)_{1*2*3*}" ] ];; gap> tblG:= CharacterTable( "6.L3(4)" );; gap> result:= [];; gap> for input in inputs do > tblsG2:= input{ [ 1 .. 3 ] }; > lib:= CharacterTable( input[4] ); > poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, input[4], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > Append( result, RepresentativesCharacterTables( poss ) ); > od; #I excluded cand. 2 (out of 8) for 6.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 3 (out of 8) for 6.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 4 (out of 8) for 6.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 5 (out of 8) for 6.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 6 (out of 8) for 6.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 7 (out of 8) for 6.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 2 (out of 8) for 6.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 3 (out of 8) for 6.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 4 (out of 8) for 6.L3(4).(2^2)_{12*3*} by 7-mod. table #I excluded cand. 5 (out of 8) for 6.L3(4).(2^2)_{12*3*} by 7-mod. table #I excluded cand. 6 (out of 8) for 6.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 7 (out of 8) for 6.L3(4).(2^2)_{12*3*} by 5-mod. table #I excluded cand. 2 (out of 8) for 6.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 3 (out of 8) for 6.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 4 (out of 8) for 6.L3(4).(2^2)_{1*2*3} by 7-mod. table #I excluded cand. 5 (out of 8) for 6.L3(4).(2^2)_{1*2*3} by 7-mod. table #I excluded cand. 6 (out of 8) for 6.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 7 (out of 8) for 6.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 2 (out of 8) for 6.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 3 (out of 8) for 6.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 4 (out of 8) for 6.L3(4).(2^2)_{1*23*} by 7-mod. table #I excluded cand. 5 (out of 8) for 6.L3(4).(2^2)_{1*23*} by 7-mod. table #I excluded cand. 6 (out of 8) for 6.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 7 (out of 8) for 6.L3(4).(2^2)_{1*23*} by 5-mod. table gap> result:= List( result, x -> x.table ); [ CharacterTable( "new6.L3(4).(2^2)_{123}" ), CharacterTable( "new6.L3(4).(2^2)_{12*3}" ), CharacterTable( "new6.L3(4).(2^2)_{123*}" ), CharacterTable( "new6.L3(4).(2^2)_{12*3*}" ), CharacterTable( "new6.L3(4).(2^2)_{1*23}" ), CharacterTable( "new6.L3(4).(2^2)_{1*2*3}" ), CharacterTable( "new6.L3(4).(2^2)_{1*23*}" ), CharacterTable( "new6.L3(4).(2^2)_{1*2*3*}" ) ]
As in Section 2.6-4, we get exactly one character table for each input, and the eight solutions lie in two orbits under isoclinism.
gap> List( result, NrConjugacyClasses ); [ 59, 53, 53, 59, 53, 59, 59, 53 ] gap> t:= result[1];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 7, 6, 4 ] gap> t:= result[2];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 8, 5, 3 ]
Up to now, it is not clear that the character tables we have constructed are really the character tables of some groups. The existence of groups for the first orbit of character tables can be established as follows.
We have shown in Section 2.6-4 that the maximal subgroups \(M\) of the type \(L_3(4).2^2\) in \(U_6(2).2\) lift to double covers \(2.L_3(4).2^2\) in \(2.U_6(2).2\). The preimages of these groups under the natural epimorphism from \(6.U_6(2).2\) have the structure \(6.L_3(4).2^2\), where the derived subgroup is the six-fold cover of \(L_3(4)\); this follows from the fact that \(6.U_6(2)\) does not admit a class fusion from the double cover \(2.L_3(4)\).
gap> 2l34:= CharacterTable( "2.L3(4)" );; gap> 6u:= CharacterTable( "6.U6(2)" );; gap> cand:= PossibleClassFusions( 2l34, 6u ); [ ]
This establishes the first and the fourth result as character tables of subgroups of \(6.U_6(2)\) and its isoclinic variant, respectively.
gap> 6u2:= CharacterTable( "6.U6(2).2" );; gap> fus:= List( result, x -> PossibleClassFusions( x, 6u2 ) );; gap> List( fus, Length ); [ 8, 0, 0, 0, 0, 0, 0, 0 ] gap> 6u2iso:= CharacterTableIsoclinic( 6u2 );; gap> fus:= List( result, x -> PossibleClassFusions( x, 6u2iso ) );; gap> List( fus, Length ); [ 0, 0, 0, 8, 0, 0, 0, 0 ]
Similarly, the group \(G_2(4).2\) contains a maximal subgroup \(M\) of the type \(3.L_3(4).2^2\), see [CCN+85, p. 97]. Its derived subgroup \(M'\) of the type \(3.L_3(4)\) lies inside \(G_2(4)\), and the preimage of \(M'\) under the natural epimorphism from \(2.G_2(4)\) to \(G_2(4)\) is a double cover of \(3.L_3(4)\), because \(3.L_3(4)\) does not admit a class fusion into \(2.G_2(4).2\).
gap> 3l34:= CharacterTable( "3.L3(4)" );; gap> g2:= CharacterTable( "G2(4).2" );; gap> 2g2:= CharacterTable( "2.G2(4).2" );; gap> PossibleClassFusions( 3l34, 2g2 ); [ ]
Only the third and eighth of our result tables admit a class fusion into \(2.G_2(4).2\) and its isoclinic variant, respectively. This shows the existence of groups for the tables from the second orbit.
gap> fus:= List( result, x -> PossibleClassFusions( x, 2g2 ) );; gap> List( fus, Length ); [ 0, 0, 16, 0, 0, 0, 0, 0 ] gap> 2g2iso:= CharacterTableIsoclinic( 2g2 );; gap> fus:= List( result, x -> PossibleClassFusions( x, 2g2iso ) );; gap> List( fus, Length ); [ 0, 0, 0, 0, 0, 0, 0, 16 ]
Now we try the second approach and compare the results.
gap> names:= [ "L3(4).(2^2)_{123}", "L3(4).(2^2)_{12*3}", > "L3(4).(2^2)_{123*}", "L3(4).(2^2)_{12*3*}" ];; gap> inputs1:= List( names, nam -> [ "6.L3(4).2_1", "2.L3(4).2_1", > Concatenation( "2.", nam ), Concatenation( "6.", nam ) ] );; gap> names:= List( names, nam -> ReplacedString( nam, "1", "1*" ) );; gap> inputs2:= List( names, nam -> [ "6.L3(4).2_1*", "2.L3(4).2_1*", > Concatenation( "2.", nam ), Concatenation( "6.", nam ) ] );; gap> inputs:= Concatenation( inputs1, inputs2 ); [ [ "6.L3(4).2_1", "2.L3(4).2_1", "2.L3(4).(2^2)_{123}", "6.L3(4).(2^2)_{123}" ], [ "6.L3(4).2_1", "2.L3(4).2_1", "2.L3(4).(2^2)_{12*3}", "6.L3(4).(2^2)_{12*3}" ], [ "6.L3(4).2_1", "2.L3(4).2_1", "2.L3(4).(2^2)_{123*}", "6.L3(4).(2^2)_{123*}" ], [ "6.L3(4).2_1", "2.L3(4).2_1", "2.L3(4).(2^2)_{12*3*}", "6.L3(4).(2^2)_{12*3*}" ], [ "6.L3(4).2_1*", "2.L3(4).2_1*", "2.L3(4).(2^2)_{1*23}", "6.L3(4).(2^2)_{1*23}" ], [ "6.L3(4).2_1*", "2.L3(4).2_1*", "2.L3(4).(2^2)_{1*2*3}", "6.L3(4).(2^2)_{1*2*3}" ], [ "6.L3(4).2_1*", "2.L3(4).2_1*", "2.L3(4).(2^2)_{1*23*}", "6.L3(4).(2^2)_{1*23*}" ], [ "6.L3(4).2_1*", "2.L3(4).2_1*", "2.L3(4).(2^2)_{1*2*3*}", "6.L3(4).(2^2)_{1*2*3*}" ] ] gap> result2:= [];; gap> for input in inputs do > tblMG := CharacterTable( input[1] ); > tblG := CharacterTable( input[2] ); > tblGA := CharacterTable( input[3] ); > name := Concatenation( "new", input[4] ); > lib := CharacterTable( input[4] ); > poss:= ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib ); > Append( result2, poss ); > od; gap> result2:= List( result2, x -> x.table ); [ CharacterTable( "new6.L3(4).(2^2)_{123}" ), CharacterTable( "new6.L3(4).(2^2)_{12*3}" ), CharacterTable( "new6.L3(4).(2^2)_{123*}" ), CharacterTable( "new6.L3(4).(2^2)_{12*3*}" ), CharacterTable( "new6.L3(4).(2^2)_{1*23}" ), CharacterTable( "new6.L3(4).(2^2)_{1*2*3}" ), CharacterTable( "new6.L3(4).(2^2)_{1*23*}" ), CharacterTable( "new6.L3(4).(2^2)_{1*2*3*}" ) ] gap> trans:= List( [ 1 .. 8 ], i -> > TransformingPermutationsCharacterTables( result[i], > result2[i] ) );; gap> ForAll( trans, IsRecord ); true
The outer automorphism group of the group \(U_4(3)\) is a dihedral group of order \(8\). There are two almost simple groups of the type \(U_4(3).2^2\), up to isomorphism, denoted as \(U_4(3).(2^2)_{122}\) and \(U_4(3).(2^2)_{133}\), respectively. Note that \(U_4(3).2_1\) is the extension by the central involution of the outer automorphism group of \(U_4(3)\), the other two subgroups of index two in \(U_4(3).(2^2)_{122}\) are \(U_4(3).2_2\) and \(U_4(3).2^{\prime}_2\), respectively, and the other two subgroups of index two in \(U_4(3).(2^2)_{133}\) are \(U_4(3).2_3\) and \(U_4(3).2^{\prime}_3\), respectively.
Since Aut\(( U_4(3) )\) possesses a double cover (see [CCN+85, p. 52]), double covers of \(U_4(3).(2^2)_{122}\) and \(U_4(3).(2^2)_{133}\) exist.
First we deal with the double covers of \(U_4(3).(2^2)_{122}\). Any such group contains one subgroup of the type \(2.U_4(3).2_1\) and two subgroups of the type \(2.U_4(3).2_2\), and there are two isoclinic variants of each of these group to consider, see Section 2.2-6. Thus we start with six different inputs for the construction of the character tables of double covers.
gap> tbls:= List( [ "1", "2", "2'" ], i -> > CharacterTable( Concatenation( "2.U4(3).2_", i ) ) );; gap> isos:= List( [ "1", "2", "2'" ], i -> > CharacterTable( Concatenation( "Isoclinic(2.U4(3).2_", i, ")" ) ) );; gap> inputs:= [ > [ tbls[1], tbls[2], tbls[3], "2.U4(3).(2^2)_{122}" ], > [ isos[1], tbls[2], tbls[3], "2.U4(3).(2^2)_{1*22}" ], > [ tbls[1], isos[2], tbls[3], "2.U4(3).(2^2)_{12*2}" ], > [ isos[1], isos[2], tbls[3], "2.U4(3).(2^2)_{1*2*2}" ], > [ tbls[1], isos[2], isos[3], "2.U4(3).(2^2)_{12*2*}" ], > [ isos[1], isos[2], isos[3], "2.U4(3).(2^2)_{1*2*2*}" ] ];; gap> tblG:= CharacterTable( "2.U4(3)" );; gap> result:= [];; gap> for input in inputs do > tblsG2:= input{ [ 1 .. 3 ] }; > lib:= CharacterTable( input[4] ); > poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, input[4], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > Append( result, RepresentativesCharacterTables( poss ) ); > od; gap> result:= List( result, x -> x.table ); [ CharacterTable( "new2.U4(3).(2^2)_{122}" ), CharacterTable( "new2.U4(3).(2^2)_{1*22}" ), CharacterTable( "new2.U4(3).(2^2)_{12*2}" ), CharacterTable( "new2.U4(3).(2^2)_{1*2*2}" ), CharacterTable( "new2.U4(3).(2^2)_{12*2*}" ), CharacterTable( "new2.U4(3).(2^2)_{1*2*2*}" ) ]
We get exactly one character table for each input. For each of these tables, there are three possibilities to form an isoclinic table, corresponding to the three subgroups of index two. It turns out that the six solutions form two orbits under forming some isoclinic table. Tables in different orbits are essentially different, already their numbers of conjugacy classes differ.
gap> List( result, NrConjugacyClasses ); [ 87, 102, 102, 87, 87, 102 ] gap> t:= result[1];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 4, 4, 5 ] gap> t:= result[2];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 3, 3, 6 ]
Up to now, it is not clear that the character tables we have constructed are really the character tables of some groups. The existence of groups for the first orbit of character tables can be established as follows.
The group \(O_8^+(3)\) contains maximal subgroups of the type \(2.U_4(3).2^2\), see [CCN+85, p. 140]. Only the first of our result tables admits a class fusion into the table of \(O_8^+(3)\).
gap> u:= CharacterTable( "O8+(3)" );; gap> fus:= List( result, x -> PossibleClassFusions( x, u ) );; gap> List( fus, Length ); [ 24, 0, 0, 0, 0, 0 ]
A table in the second orbit belongs to a maximal subgroup of \(O_7(3).2\), see [CCN+85, p. 109].
gap> u:= CharacterTable( "O7(3).2" );; gap> fus:= List( result, x -> PossibleClassFusions( x, u ) );; gap> List( fus, Length ); [ 0, 16, 0, 0, 0, 0 ]
Note that this subgroup of \(O_7(3).2 \cong SO(7,3)\) is the orthogonal group GO\(_6^-(3)\).
Now we deal with the double covers of \(U_4(3).(2^2)_{133}\). The constructions of the character tables are completely analogous to those in the case of \(U_4(3).(2^2)_{122}\).
gap> tbls:= List( [ "1", "3", "3'" ], > i -> CharacterTable( Concatenation( "2.U4(3).2_", i ) ) );; gap> isos:= List( [ "1", "3", "3'" ], i -> > CharacterTable( Concatenation( "Isoclinic(2.U4(3).2_", i, ")" ) ) );; gap> inputs:= [ > [ tbls[1], tbls[2], tbls[3], "2.U4(3).(2^2)_{133}" ], > [ isos[1], tbls[2], tbls[3], "2.U4(3).(2^2)_{1*33}" ], > [ tbls[1], isos[2], tbls[3], "2.U4(3).(2^2)_{13*3}" ], > [ isos[1], isos[2], tbls[3], "2.U4(3).(2^2)_{1*3*3}" ], > [ tbls[1], isos[2], isos[3], "2.U4(3).(2^2)_{13*3*}" ], > [ isos[1], isos[2], isos[3], "2.U4(3).(2^2)_{1*3*3*}" ] ];; gap> tblG:= CharacterTable( "2.U4(3)" );; gap> result:= [];; gap> for input in inputs do > tblsG2:= input{ [ 1 .. 3 ] }; > lib:= CharacterTable( input[4] ); > poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, input[4], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > Append( result, RepresentativesCharacterTables( poss ) ); > od; #I excluded cand. 2 (out of 4) for 2.U4(3).(2^2)_{1*33} by 3-mod. table #I excluded cand. 3 (out of 4) for 2.U4(3).(2^2)_{1*33} by 3-mod. table #I excluded cand. 2 (out of 4) for 2.U4(3).(2^2)_{13*3} by 3-mod. table #I excluded cand. 3 (out of 4) for 2.U4(3).(2^2)_{13*3} by 3-mod. table #I excluded cand. 2 (out of 4) for 2.U4(3).(2^2)_{1*3*3*} by 3-mod. table #I excluded cand. 3 (out of 4) for 2.U4(3).(2^2)_{1*3*3*} by 3-mod. table gap> result:= List( result, x -> x.table ); [ CharacterTable( "new2.U4(3).(2^2)_{133}" ), CharacterTable( "new2.U4(3).(2^2)_{1*33}" ), CharacterTable( "new2.U4(3).(2^2)_{13*3}" ), CharacterTable( "new2.U4(3).(2^2)_{1*3*3}" ), CharacterTable( "new2.U4(3).(2^2)_{13*3*}" ), CharacterTable( "new2.U4(3).(2^2)_{1*3*3*}" ) ] gap> List( result, NrConjugacyClasses ); [ 69, 72, 72, 69, 69, 72 ] gap> t:= result[1];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 4, 4, 5 ] gap> t:= result[2];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 3, 3, 6 ]
The situation with \(4_1.L_3(4).2^2\) is analogous to that with \(6.L_3(4).2^2\), see Section 2.6-5.
gap> tbls:= List( [ "1", "2", "3" ], > i -> CharacterTable( Concatenation( "4_1.L3(4).2_", i ) ) ); [ CharacterTable( "4_1.L3(4).2_1" ), CharacterTable( "4_1.L3(4).2_2" ) , CharacterTable( "4_1.L3(4).2_3" ) ] gap> isos:= List( [ "1", "2", "3" ], > i -> CharacterTable( Concatenation( "4_1.L3(4).2_", i, "*" ) ) ); [ CharacterTable( "Isoclinic(4_1.L3(4).2_1)" ), CharacterTable( "Isoclinic(4_1.L3(4).2_2)" ), CharacterTable( "4_1.L3(4).2_3*" ) ]
Note that the group \(4_1.L_3(4).2_3\) has a centre of order four, so one cannot construct the isoclinic variant by calling the one argument version of CharacterTableIsoclinic (Reference: CharacterTableIsoclinic).
gap> List( tbls, ClassPositionsOfCentre ); [ [ 1, 3 ], [ 1, 3 ], [ 1, 2, 3, 4 ] ] gap> IsRecord( TransformingPermutationsCharacterTables( tbls[3], > CharacterTableIsoclinic( tbls[3] ) ) ); true
Again, we get eight different character tables, in two orbits.
gap> inputs:= [ > [ tbls[1], tbls[2], tbls[3], "4_1.L3(4).(2^2)_{123}" ], > [ isos[1], tbls[2], tbls[3], "4_1.L3(4).(2^2)_{1*23}" ], > [ tbls[1], isos[2], tbls[3], "4_1.L3(4).(2^2)_{12*3}" ], > [ isos[1], isos[2], tbls[3], "4_1.L3(4).(2^2)_{1*2*3}" ], > [ tbls[1], tbls[2], isos[3], "4_1.L3(4).(2^2)_{123*}" ], > [ isos[1], tbls[2], isos[3], "4_1.L3(4).(2^2)_{1*23*}" ], > [ tbls[1], isos[2], isos[3], "4_1.L3(4).(2^2)_{12*3*}" ], > [ isos[1], isos[2], isos[3], "4_1.L3(4).(2^2)_{1*2*3*}" ] ];; gap> tblG:= CharacterTable( "4_1.L3(4)" );; gap> result:= [];; gap> for input in inputs do > tblsG2:= input{ [ 1 .. 3 ] }; > lib:= CharacterTable( input[4] ); > poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, input[4], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > Append( result, RepresentativesCharacterTables( poss ) ); > od; #I excluded cand. 2 (out of 8) for 4_1.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_1.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_1.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_1.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_1.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_1.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 2 (out of 8) for 4_1.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_1.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_1.L3(4).(2^2)_{1*23} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_1.L3(4).(2^2)_{1*23} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_1.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_1.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 2 (out of 8) for 4_1.L3(4).(2^2)_{12*3} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_1.L3(4).(2^2)_{12*3} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_1.L3(4).(2^2)_{12*3} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_1.L3(4).(2^2)_{12*3} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_1.L3(4).(2^2)_{12*3} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_1.L3(4).(2^2)_{12*3} by 5-mod. table #I excluded cand. 2 (out of 8) for 4_1.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_1.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_1.L3(4).(2^2)_{1*2*3} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_1.L3(4).(2^2)_{1*2*3} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_1.L3(4).(2^2)_{1*2*3} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_1.L3(4).(2^2)_{1*2*3} by 5-mod. table gap> result:= List( result, x -> x.table ); [ CharacterTable( "new4_1.L3(4).(2^2)_{123}" ), CharacterTable( "new4_1.L3(4).(2^2)_{1*23}" ), CharacterTable( "new4_1.L3(4).(2^2)_{12*3}" ), CharacterTable( "new4_1.L3(4).(2^2)_{1*2*3}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123*}" ), CharacterTable( "new4_1.L3(4).(2^2)_{1*23*}" ), CharacterTable( "new4_1.L3(4).(2^2)_{12*3*}" ), CharacterTable( "new4_1.L3(4).(2^2)_{1*2*3*}" ) ] gap> List( result, NrConjugacyClasses ); [ 48, 48, 48, 48, 42, 42, 42, 42 ] gap> t:= result[1];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 3, 2, 4 ] gap> t:= result[5];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 7, 6, 8 ]
Note that only two out of the eight tables of the type \(2.L_3(4).2^2\) occur as factors of the eight tables.
gap> facts:= [ CharacterTable( "2.L3(4).(2^2)_{123}" ), > CharacterTable( "2.L3(4).(2^2)_{123*}" ) ];; gap> factresults:= List( result, t -> t / ClassPositionsOfCentre( t ) );; gap> List( factresults, t -> PositionProperty( facts, f -> > IsRecord( TransformingPermutationsCharacterTables( t, f ) ) ) ); [ 1, 1, 1, 1, 2, 2, 2, 2 ]
This is not surprising; note that for \(1 \leq i \leq 2\), the two isoclinic variants of \(4_1.L_3(4).2_i\) have isomorphic factor groups of the type \(2.L_3(4).2_i\). (For \(i = 3\), this is not the case.)
gap> test:= [ CharacterTable( "4_1.L3(4).2_1" ), > CharacterTable( "4_1.L3(4).2_1*" ) ];; gap> List( test, ClassPositionsOfCentre ); [ [ 1, 3 ], [ 1, 3 ] ] gap> fact:= List( test, t -> t / ClassPositionsOfCentre( t ) );; gap> IsRecord( TransformingPermutationsCharacterTables( fact[1], fact[2] ) ); true gap> test:= [ CharacterTable( "4_1.L3(4).2_2" ), > CharacterTable( "4_1.L3(4).2_2*" ) ];; gap> List( test, ClassPositionsOfCentre ); [ [ 1, 3 ], [ 1, 3 ] ] gap> fact:= List( test, t -> t / ClassPositionsOfCentre( t ) );; gap> IsRecord( TransformingPermutationsCharacterTables( fact[1], fact[2] ) ); true
Now we try the second approach and compare the results. By the abovementioned asymmetry, it is clear that the tables are not uniquely determined by the input data.
gap> names:= [ "L3(4).(2^2)_{123}", "L3(4).(2^2)_{1*23}", > "L3(4).(2^2)_{12*3}", "L3(4).(2^2)_{1*2*3}" ];; gap> inputs1:= List( names, nam -> [ "4_1.L3(4).2_3", "2.L3(4).2_3", > Concatenation( "2.", nam ), Concatenation( "4_1.", nam ) ] );; gap> names:= List( names, nam -> ReplacedString( nam, "3}", "3*}" ) );; gap> inputs2:= List( names, nam -> [ "4_1.L3(4).2_3*", "2.L3(4).2_3*", > Concatenation( "2.", nam ), Concatenation( "4_1.", nam ) ] );; gap> inputs:= Concatenation( inputs1, inputs2 ); [ [ "4_1.L3(4).2_3", "2.L3(4).2_3", "2.L3(4).(2^2)_{123}", "4_1.L3(4).(2^2)_{123}" ], [ "4_1.L3(4).2_3", "2.L3(4).2_3", "2.L3(4).(2^2)_{1*23}", "4_1.L3(4).(2^2)_{1*23}" ], [ "4_1.L3(4).2_3", "2.L3(4).2_3", "2.L3(4).(2^2)_{12*3}", "4_1.L3(4).(2^2)_{12*3}" ], [ "4_1.L3(4).2_3", "2.L3(4).2_3", "2.L3(4).(2^2)_{1*2*3}", "4_1.L3(4).(2^2)_{1*2*3}" ], [ "4_1.L3(4).2_3*", "2.L3(4).2_3*", "2.L3(4).(2^2)_{123*}", "4_1.L3(4).(2^2)_{123*}" ], [ "4_1.L3(4).2_3*", "2.L3(4).2_3*", "2.L3(4).(2^2)_{1*23*}", "4_1.L3(4).(2^2)_{1*23*}" ], [ "4_1.L3(4).2_3*", "2.L3(4).2_3*", "2.L3(4).(2^2)_{12*3*}", "4_1.L3(4).(2^2)_{12*3*}" ], [ "4_1.L3(4).2_3*", "2.L3(4).2_3*", "2.L3(4).(2^2)_{1*2*3*}", "4_1.L3(4).(2^2)_{1*2*3*}" ] ] gap> result2:= [];; gap> for input in inputs do > tblMG := CharacterTable( input[1] ); > tblG := CharacterTable( input[2] ); > tblGA := CharacterTable( input[3] ); > name := Concatenation( "new", input[4] ); > lib := CharacterTable( input[4] ); > poss:= ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib ); > Append( result2, poss ); > od; #E 4 possibilities for new4_1.L3(4).(2^2)_{123} #E no solution for new4_1.L3(4).(2^2)_{1*23} #E no solution for new4_1.L3(4).(2^2)_{12*3} #E no solution for new4_1.L3(4).(2^2)_{1*2*3} #E 4 possibilities for new4_1.L3(4).(2^2)_{123*} #E no solution for new4_1.L3(4).(2^2)_{1*23*} #E no solution for new4_1.L3(4).(2^2)_{12*3*} #E no solution for new4_1.L3(4).(2^2)_{1*2*3*} gap> Length( result2 ); 8 gap> result2:= List( result2, x -> x.table ); [ CharacterTable( "new4_1.L3(4).(2^2)_{123}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123*}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123*}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123*}" ), CharacterTable( "new4_1.L3(4).(2^2)_{123*}" ) ] gap> List( result, t1 -> PositionsProperty( result2, t2 -> IsRecord( > TransformingPermutationsCharacterTables( t1, t2 ) ) ) ); [ [ 1 ], [ 4 ], [ 3 ], [ 2 ], [ 7 ], [ 6 ], [ 5 ], [ 8 ] ]
At the moment, I do not know interesting groups that contain one of the \(4_1.L_3(4).2^2\) type groups and whose character tables are available.
The situation with \(4_2.L_3(4).2^2\) is analogous to that with \(6.L_3(4).2^2\), see Section 2.6-5.
gap> tbls:= List( [ "1", "2", "3" ], > i -> CharacterTable( Concatenation( "4_2.L3(4).2_", i ) ) ); [ CharacterTable( "4_2.L3(4).2_1" ), CharacterTable( "4_2.L3(4).2_2" ) , CharacterTable( "4_2.L3(4).2_3" ) ] gap> isos:= List( [ "1", "2", "3" ], > i -> CharacterTable( Concatenation( "4_2.L3(4).2_", i, "*" ) ) ); [ CharacterTable( "Isoclinic(4_2.L3(4).2_1)" ), CharacterTable( "4_2.L3(4).2_2*" ), CharacterTable( "Isoclinic(4_2.L3(4).2_3)" ) ]
Note that the group \(4_1.L_3(4).2_2\) has a centre of order four, so one cannot construct the isoclinic variant not by calling the one argument version of CharacterTableIsoclinic (Reference: CharacterTableIsoclinic).
gap> List( tbls, ClassPositionsOfCentre ); [ [ 1, 3 ], [ 1, 2, 3, 4 ], [ 1, 3 ] ] gap> IsRecord( TransformingPermutationsCharacterTables( tbls[2], > CharacterTableIsoclinic( tbls[2] ) ) ); true
Again, we get eight different character tables, in two orbits.
gap> inputs:= [ > [ tbls[1], tbls[2], tbls[3], "4_2.L3(4).(2^2)_{123}" ], > [ isos[1], tbls[2], tbls[3], "4_2.L3(4).(2^2)_{1*23}" ], > [ tbls[1], isos[2], tbls[3], "4_2.L3(4).(2^2)_{12*3}" ], > [ tbls[1], tbls[2], isos[3], "4_2.L3(4).(2^2)_{123*}" ], > [ isos[1], isos[2], tbls[3], "4_2.L3(4).(2^2)_{1*2*3}" ], > [ isos[1], tbls[2], isos[3], "4_2.L3(4).(2^2)_{1*23*}" ], > [ tbls[1], isos[2], isos[3], "4_2.L3(4).(2^2)_{12*3*}" ], > [ isos[1], isos[2], isos[3], "4_2.L3(4).(2^2)_{1*2*3*}" ] ];; gap> tblG:= CharacterTable( "4_2.L3(4)" );; gap> result:= [];; gap> for input in inputs do > tblsG2:= input{ [ 1 .. 3 ] }; > lib:= CharacterTable( input[4] ); > poss:= ConstructOrdinaryGV4Table( tblG, tblsG2, input[4], lib ); > ConstructModularGV4Tables( tblG, tblsG2, poss, lib ); > Append( result, RepresentativesCharacterTables( poss ) ); > od; #I excluded cand. 2 (out of 8) for 4_2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_2.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_2.L3(4).(2^2)_{123} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_2.L3(4).(2^2)_{123} by 5-mod. table #I excluded cand. 2 (out of 8) for 4_2.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_2.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_2.L3(4).(2^2)_{1*23} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_2.L3(4).(2^2)_{1*23} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_2.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_2.L3(4).(2^2)_{1*23} by 5-mod. table #I excluded cand. 2 (out of 8) for 4_2.L3(4).(2^2)_{123*} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_2.L3(4).(2^2)_{123*} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_2.L3(4).(2^2)_{123*} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_2.L3(4).(2^2)_{123*} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_2.L3(4).(2^2)_{123*} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_2.L3(4).(2^2)_{123*} by 5-mod. table #I excluded cand. 2 (out of 8) for 4_2.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 3 (out of 8) for 4_2.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 4 (out of 8) for 4_2.L3(4).(2^2)_{1*23*} by 7-mod. table #I excluded cand. 5 (out of 8) for 4_2.L3(4).(2^2)_{1*23*} by 7-mod. table #I excluded cand. 6 (out of 8) for 4_2.L3(4).(2^2)_{1*23*} by 5-mod. table #I excluded cand. 7 (out of 8) for 4_2.L3(4).(2^2)_{1*23*} by 5-mod. table gap> result:= List( result, x -> x.table ); [ CharacterTable( "new4_2.L3(4).(2^2)_{123}" ), CharacterTable( "new4_2.L3(4).(2^2)_{1*23}" ), CharacterTable( "new4_2.L3(4).(2^2)_{12*3}" ), CharacterTable( "new4_2.L3(4).(2^2)_{123*}" ), CharacterTable( "new4_2.L3(4).(2^2)_{1*2*3}" ), CharacterTable( "new4_2.L3(4).(2^2)_{1*23*}" ), CharacterTable( "new4_2.L3(4).(2^2)_{12*3*}" ), CharacterTable( "new4_2.L3(4).(2^2)_{1*2*3*}" ) ] gap> List( result, NrConjugacyClasses ); [ 50, 50, 44, 50, 44, 50, 44, 44 ] gap> t:= result[1];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 4, 2, 6 ] gap> t:= result[3];; gap> nsg:= Filtered( ClassPositionsOfNormalSubgroups( t ), > x -> Sum( SizesConjugacyClasses( t ){ x } ) = Size( t ) / 2 );; gap> iso:= List( nsg, x -> CharacterTableIsoclinic( t, x ) );; gap> List( iso, x -> PositionProperty( result, y -> > TransformingPermutationsCharacterTables( x, y ) <> fail ) ); [ 7, 5, 8 ]
Note that only two out of the eight tables of the type \(2.L_3(4).2^2\) occur as factors of the eight tables.
gap> facts:= [ CharacterTable( "2.L3(4).(2^2)_{123}" ), > CharacterTable( "2.L3(4).(2^2)_{12*3}" ) ];; gap> factresults:= List( result, t -> t / ClassPositionsOfCentre( t ) );; gap> List( factresults, t -> PositionProperty( facts, f -> > IsRecord( TransformingPermutationsCharacterTables( t, f ) ) ) ); [ 1, 1, 2, 1, 2, 1, 2, 2 ]
This is not surprising; note that for \(i \in \{ 1, 3 \}\), the two isoclinic variants of \(4_1.L_3(4).2_i\) have isomorphic factor groups of the type \(2.L_3(4).2_i\). (For \(i = 2\), this is not the case.)
gap> test:= [ CharacterTable( "4_2.L3(4).2_1" ), > CharacterTable( "4_2.L3(4).2_1*" ) ];; gap> List( test, ClassPositionsOfCentre ); [ [ 1, 3 ], [ 1, 3 ] ] gap> fact:= List( test, t -> t / ClassPositionsOfCentre( t ) );; gap> IsRecord( TransformingPermutationsCharacterTables( fact[1], fact[2] ) ); true gap> test:= [ CharacterTable( "4_2.L3(4).2_3" ), > CharacterTable( "4_2.L3(4).2_3*" ) ];; gap> List( test, ClassPositionsOfCentre ); [ [ 1, 3 ], [ 1, 3 ] ] gap> fact:= List( test, t -> t / ClassPositionsOfCentre( t ) );; gap> IsRecord( TransformingPermutationsCharacterTables( fact[1], fact[2] ) ); true
Now we try the second approach and compare the results. By the abovementioned asymmetry, it is clear that the tables are not uniquely determined by the input data.
gap> names:= [ "L3(4).(2^2)_{123}", "L3(4).(2^2)_{1*23}", > "L3(4).(2^2)_{123*}", "L3(4).(2^2)_{1*23*}" ];; gap> inputs1:= List( names, nam -> [ "4_2.L3(4).2_2", "2.L3(4).2_2", > Concatenation( "2.", nam ), Concatenation( "4_2.", nam ) ] );; gap> names:= List( names, nam -> ReplacedString( nam, "23", "2*3" ) );; gap> inputs2:= List( names, nam -> [ "4_2.L3(4).2_2*", "2.L3(4).2_2*", > Concatenation( "2.", nam ), Concatenation( "4_2.", nam ) ] );; gap> inputs:= Concatenation( inputs1, inputs2 ); [ [ "4_2.L3(4).2_2", "2.L3(4).2_2", "2.L3(4).(2^2)_{123}", "4_2.L3(4).(2^2)_{123}" ], [ "4_2.L3(4).2_2", "2.L3(4).2_2", "2.L3(4).(2^2)_{1*23}", "4_2.L3(4).(2^2)_{1*23}" ], [ "4_2.L3(4).2_2", "2.L3(4).2_2", "2.L3(4).(2^2)_{123*}", "4_2.L3(4).(2^2)_{123*}" ], [ "4_2.L3(4).2_2", "2.L3(4).2_2", "2.L3(4).(2^2)_{1*23*}", "4_2.L3(4).(2^2)_{1*23*}" ], [ "4_2.L3(4).2_2*", "2.L3(4).2_2*", "2.L3(4).(2^2)_{12*3}", "4_2.L3(4).(2^2)_{12*3}" ], [ "4_2.L3(4).2_2*", "2.L3(4).2_2*", "2.L3(4).(2^2)_{1*2*3}", "4_2.L3(4).(2^2)_{1*2*3}" ], [ "4_2.L3(4).2_2*", "2.L3(4).2_2*", "2.L3(4).(2^2)_{12*3*}", "4_2.L3(4).(2^2)_{12*3*}" ], [ "4_2.L3(4).2_2*", "2.L3(4).2_2*", "2.L3(4).(2^2)_{1*2*3*}", "4_2.L3(4).(2^2)_{1*2*3*}" ] ] gap> result2:= [];; gap> for input in inputs do > tblMG := CharacterTable( input[1] ); > tblG := CharacterTable( input[2] ); > tblGA := CharacterTable( input[3] ); > name := Concatenation( "new", input[4] ); > lib := CharacterTable( input[4] ); > poss:= ConstructOrdinaryMGATable( tblMG, tblG, tblGA, name, lib ); > Append( result2, poss ); > od; #E 4 possibilities for new4_2.L3(4).(2^2)_{123} #E no solution for new4_2.L3(4).(2^2)_{1*23} #E no solution for new4_2.L3(4).(2^2)_{123*} #E no solution for new4_2.L3(4).(2^2)_{1*23*} #E 4 possibilities for new4_2.L3(4).(2^2)_{12*3} #E no solution for new4_2.L3(4).(2^2)_{1*2*3} #E no solution for new4_2.L3(4).(2^2)_{12*3*} #E no solution for new4_2.L3(4).(2^2)_{1*2*3*} gap> Length( result2 ); 8 gap> result2:= List( result2, x -> x.table ); [ CharacterTable( "new4_2.L3(4).(2^2)_{123}" ), CharacterTable( "new4_2.L3(4).(2^2)_{123}" ), CharacterTable( "new4_2.L3(4).(2^2)_{123}" ), CharacterTable( "new4_2.L3(4).(2^2)_{123}" ), CharacterTable( "new4_2.L3(4).(2^2)_{12*3}" ), CharacterTable( "new4_2.L3(4).(2^2)_{12*3}" ), CharacterTable( "new4_2.L3(4).(2^2)_{12*3}" ), CharacterTable( "new4_2.L3(4).(2^2)_{12*3}" ) ] gap> List( result, t1 -> PositionsProperty( result2, t2 -> IsRecord( > TransformingPermutationsCharacterTables( t1, t2 ) ) ) ); [ [ 1 ], [ 4 ], [ 7 ], [ 3 ], [ 6 ], [ 2 ], [ 5 ], [ 8 ] ]
The group \(ON.2\) contains a maximal subgroup \(M\) of the type \(4_2.L_3(4).2^2\), see [CCN+85, p. 132]. Only the third result table admits a class fusion into \(ON.2\). This shows the existence of groups for the tables from the second orbit.
gap> on2:= CharacterTable( "ON.2" );; gap> fus:= List( result, x -> PossibleClassFusions( x, on2 ) );; gap> List( fus, Length ); [ 0, 0, 16, 0, 0, 0, 0, 0 ]
The group Aut\((L_2(81)) \cong L_2(81).(2 \times 4)\) has the structure \(G.2^2\) where \(G = L_2(81).2_1\). Here we get two triples of possible actions on the tables of the groups \(G.2_i\), and one possible character table for each triple.
gap> input:= [ "L2(81).2_1", "L2(81).4_1", "L2(81).4_2", "L2(81).2^2", > "L2(81).(2x4)" ];; gap> tblG := CharacterTable( input[1] );; gap> tblsG2 := List( input{ [ 2 .. 4 ] }, CharacterTable );; gap> name := Concatenation( "new", input[5] );; gap> lib := CharacterTable( input[5] );; gap> poss := ConstructOrdinaryGV4Table( tblG, tblsG2, name, lib );; #I newL2(81).(2x4): 2 equivalence classes gap> reps:= RepresentativesCharacterTables( poss );; gap> Length( reps ); 2
Due to the different underlying actions, the power maps of the two candidate tables differ.
gap> ord:= OrdersClassRepresentatives( reps[1].table );; gap> ord = OrdersClassRepresentatives( reps[2].table ); true gap> pos:= Position( ord, 80 ); 33 gap> PowerMap( reps[1].table, 3 )[ pos ]; 34 gap> PowerMap( reps[2].table, 3 )[ pos ]; 33
Aut\((L_2(81))\) can be generated by PGL\((2,81) = L_2(81).2_2\) and the Frobenius automorphism of order four that is defined on GL\((2,81)\) as the map that cubes the matrix entries. The elements of order \(80\) in Aut\((L_2(81))\) are conjugates of diagonal matrices modulo scalar matrices, which are mapped to their third powers by the Frobenius homomorphism. So the third power map of Aut\((L_2(81))\) fixes the classes of elements of order \(80\). In other words, the second of the two tables is the right one.
gap> trans:= TransformingPermutationsCharacterTables( reps[2].table, lib );; gap> IsRecord( trans ); true gap> List( reps[2].G2fusGV4, x -> OnTuples( x, trans.columns ) ) > = List( tblsG2, x -> GetFusionMap( x, lib ) ); true gap> ConstructModularGV4Tables( tblG, tblsG2, [ reps[2] ], lib );; #I not all input tables for L2(81).(2x4) mod 41 available
The construction of the character table of the group \(O_8^+(3).2^2_{111}\) is not as straightforward as the constructions shown in Section 2.6-2. Here we get \(26\) triples of actions on the tables of the three subgroups \(G.2_i\) of index two, but only one of them leads to candidates for the desired character table. Specifically, we get \(64\) such candidates, in two equivalence classes w.r.t. permutation equivalence.
gap> input:= [ "O8+(3)", "O8+(3).2_1", "O8+(3).2_1'", "O8+(3).2_1''", > "O8+(3).(2^2)_{111}" ];; gap> tblG := CharacterTable( input[1] );; gap> tblsG2 := List( input{ [ 2 .. 4 ] }, CharacterTable );; gap> name := Concatenation( "new", input[5] );; gap> lib := CharacterTable( input[5] );; gap> poss := ConstructOrdinaryGV4Table( tblG, tblsG2, name, lib );; #I newO8+(3).(2^2)_{111}: 2 equivalence classes gap> Length( poss ); 64 gap> reps:= RepresentativesCharacterTables( poss );; gap> Length( reps ); 2
The two candidate tables differ only in four irreducible characters involving irrationalities on the classes of element order \(28\). All three subgroups \(G.2_i\) contain elements of order \(28\) that do not lie in the simple group \(G\); these classes are roots of the same (unique) class of element order \(7\). The centralizer \(C\) of an order \(7\) element in \(G.2^2\) has order \(112 = 2^4 \cdot 7\), the intersection of \(C\) with \(G\) has the structure \(2^2 \times 7\) since \(G\) contains three classes of cyclic subgroups of the order \(14\), and each of the intersections of \(C\) with one of the subgroups \(G.2_i\) has the structure \(2 \times 4 \times 7\), so the structure of \(C\) is \(4^2 \times 7 \cong 4 \times 28\).
gap> t:= reps[1].table;; gap> ord7:= Filtered( [ 1 .. NrConjugacyClasses( t ) ], > i -> OrdersClassRepresentatives( t )[i] = 7 ); [ 37 ] gap> SizesCentralizers( t ){ ord7 }; [ 112 ] gap> ord28:= Filtered( [ 1 .. NrConjugacyClasses( t ) ], > i -> OrdersClassRepresentatives( t )[i] = 28 ); [ 112, 113, 114, 115, 161, 162, 163, 164, 210, 211, 212, 213 ] gap> List( reps[1].G2fusGV4, x -> Intersection( ord28, x ) ); [ [ 112, 113, 114, 115 ], [ 161, 162, 163, 164 ], [ 210, 211, 212, 213 ] ] gap> sub:= CharacterTable( "Cyclic", 28 ) * CharacterTable( "Cyclic", 4 );; gap> List( reps, x -> Length( PossibleClassFusions( sub, x.table ) ) ); [ 0, 96 ]
It turns out that only one of the two candidate tables admits a class fusion from the character table of \(C\), thus we have determined the ordinary character table of \(O_8^+(3).2^2_{111}\). It coincides with the table from the library.
gap> trans:= TransformingPermutationsCharacterTables( reps[2].table, lib );; gap> IsRecord( trans ); true gap> List( reps[2].G2fusGV4, x -> OnTuples( x, trans.columns ) ) > = List( tblsG2, x -> GetFusionMap( x, lib ) ); true
(If we do not believe the statement about the structure of \(C\) then we can check all \(14\) groups of order \(112\) that contain a central subgroup of order \(7\). A unique such group admits a class fusion into at least one of the two candidate tables.)
The wrong candidate for the ordinary table cannot be excluded via conditions that are forced by the construction of the \(p\)-modular tables of \(O_8^+(3).2^2_{111}\). Thus we restrict the ordinary tables used for this construction to those candidates that are equivalent to the correct table.
gap> poss:= Filtered( poss, > r -> TransformingPermutationsCharacterTables( r.table, lib ) > <> fail );; gap> ConstructModularGV4Tables( tblG, tblsG2, poss, lib );; #I not all input tables for O8+(3).(2^2)_{111} mod 3 available
So also the \(p\)-modular tables of \(O_8^+(3).2^2_{111}\) can be computed this way, provided that the \(p\)-modular tables of the index \(2\) subgroups are available.
We compute the character table of a group of the type \(2^2.G\) from the character tables of the three factor groups of the type \(2.G\), using the function PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G), see Section 2.3-4.
The three central involutions in \(2^2.Sz(8)\) are permuted cyclicly by an outer automorphism \(\alpha\) of order three. In order to apply PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G), we need the character table of the group \(2.Sz(8)\) and the action on the classes of \(Sz(8)\) that is induced by \(\alpha\).
The ordinary character table of \(G = Sz(8)\) admits exactly five table automorphisms of order dividing \(3\). Each of these possibilities leads to exactly one possible character table of \(2^2.G\), and the five tables are permutation equivalent. From this point of view, we need not know which of the table automorphisms are induced by outer group automorphisms of \(G\).
gap> t:= CharacterTable( "Sz(8)" );; gap> 2t:= CharacterTable( "2.Sz(8)" );; gap> aut:= AutomorphismsOfTable( t );; gap> elms:= Set( Filtered( aut, x -> Order( x ) in [ 1, 3 ] ), > SmallestGeneratorPerm ); [ (), (9,10,11), (6,7,8), (6,7,8)(9,10,11), (6,7,8)(9,11,10) ] gap> poss:= List( elms, > pi -> PossibleCharacterTablesOfTypeV4G( t, 2t, pi, "2^2.Sz(8)" ) ); [ [ CharacterTable( "2^2.Sz(8)" ) ], [ CharacterTable( "2^2.Sz(8)" ) ] , [ CharacterTable( "2^2.Sz(8)" ) ], [ CharacterTable( "2^2.Sz(8)" ) ], [ CharacterTable( "2^2.Sz(8)" ) ] ] gap> reps:= RepresentativesCharacterTables( Concatenation( poss ) ); [ CharacterTable( "2^2.Sz(8)" ) ]
The tables coincide with the one that is stored in the GAP library.
gap> IsRecord( TransformingPermutationsCharacterTables( reps[1], > CharacterTable( "2^2.Sz(8)" ) ) ); true
The computation of the \(p\)-modular character table of \(2^2.G\) from the \(p\)-modular character table of \(2.G\) and the three factor fusions from \(2^2.G\) to \(2.G\) is straightforward, as is stated in Section 2.3-4. The three fusions are stored on the tables returned by PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G).
gap> GetFusionMap( poss[1][1], 2t, "1" ); [ 1, 1, 2, 2, 3, 4, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10, 11, 11, 12, 12, 13, 13, 14, 14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19 ] gap> GetFusionMap( poss[1][1], 2t, "2" ); [ 1, 2, 1, 2, 3, 4, 5, 6, 7, 6, 7, 8, 9, 8, 9, 10, 11, 10, 11, 12, 13, 12, 13, 14, 15, 14, 15, 16, 17, 16, 17, 18, 19, 18, 19 ] gap> GetFusionMap( poss[1][1], 2t, "3" ); [ 1, 2, 2, 1, 3, 4, 5, 6, 7, 7, 6, 8, 9, 9, 8, 10, 11, 11, 10, 12, 13, 13, 12, 14, 15, 15, 14, 16, 17, 17, 16, 18, 19, 19, 18 ]
The GAP library function BrauerTableOfTypeV4G (CTblLib: BrauerTableOfTypeV4G) can be used to derive Brauer tables of \(2^2.G\). We have to compute the \(p\)-modular tables for prime divisors \(p\) of \(|G|\), that is, for \(p \in \{ 2, 5, 7, 13 \}\).
gap> PrimeDivisors( Size( t ) ); [ 2, 5, 7, 13 ]
Clearly \(p = 2\) is uninteresting from this point of view because the \(2\)-modular table of \(2^2.G\) can be identified with the \(2\)-modular table of \(G\).
For each of the five ordinary tables (corresponding to the five possible table automorphisms of \(G\)) constructed above, we get one candidate of a \(5\)-modular table. However, these tables are not all equivalent. There are two equivalence classes, and one of the two possibilities is inconsistent in the sense that not all tensor products of irreducibles decompose into irreducibles.
gap> cand:= List( poss, l -> BrauerTableOfTypeV4G( l[1], 2t mod 5, > ConstructionInfoCharacterTable( l[1] )[3] ) ); [ BrauerTable( "2^2.Sz(8)", 5 ), BrauerTable( "2^2.Sz(8)", 5 ), BrauerTable( "2^2.Sz(8)", 5 ), BrauerTable( "2^2.Sz(8)", 5 ), BrauerTable( "2^2.Sz(8)", 5 ) ] gap> Length( RepresentativesCharacterTables( cand ) ); 2 gap> List( cand, CTblLib.Test.TensorDecomposition ); [ false, true, false, true, true ] gap> Length( RepresentativesCharacterTables( cand{ [ 2, 4, 5 ] } ) ); 1 gap> IsRecord( TransformingPermutationsCharacterTables( cand[2], > CharacterTable( "2^2.Sz(8)" ) mod 5 ) ); true
This implies that only those table automorphisms of \(G\) can be induced by an outer group automorphism that move the classes of element order \(13\).
The \(7\)-modular table of \(2^2.G\) is uniquely determined, independent of the choice of the table automorphism of \(G\).
gap> cand:= List( poss, l -> BrauerTableOfTypeV4G( l[1], 2t mod 7, > ConstructionInfoCharacterTable( l[1] )[3] ) ); [ BrauerTable( "2^2.Sz(8)", 7 ), BrauerTable( "2^2.Sz(8)", 7 ), BrauerTable( "2^2.Sz(8)", 7 ), BrauerTable( "2^2.Sz(8)", 7 ), BrauerTable( "2^2.Sz(8)", 7 ) ] gap> Length( RepresentativesCharacterTables( cand ) ); 1 gap> IsRecord( TransformingPermutationsCharacterTables( cand[1], > CharacterTable( "2^2.Sz(8)" ) mod 7 ) ); true
We get two candidates for the \(13\)-modular table of \(2^2.G\), also if we consider only the three admissible table automorphisms.
gap> elms:= elms{ [ 2, 4, 5 ] }; [ (9,10,11), (6,7,8)(9,10,11), (6,7,8)(9,11,10) ] gap> poss:= poss{ [ 2, 4, 5 ] };; gap> cand:= List( poss, l -> BrauerTableOfTypeV4G( l[1], 2t mod 13, > ConstructionInfoCharacterTable( l[1] )[3] ) ); [ BrauerTable( "2^2.Sz(8)", 13 ), BrauerTable( "2^2.Sz(8)", 13 ), BrauerTable( "2^2.Sz(8)", 13 ) ] gap> Length( RepresentativesCharacterTables( cand ) ); 2 gap> List( cand, CTblLib.Test.TensorDecomposition ); [ true, true, true ]
The action of the outer automorphism of order three of \(G\) can be read off from the \(2\)-modular table of \(G\). Note that the ordinary and the \(5\)-modular character table of \(G\) possess two independent table automorphisms of order three, whereas the group of table automorphisms of the \(2\)-modular table has order three. (The reason is that the irrational values on the classes of the element orders \(7\) and \(13\) appear in the same irreducible \(2\)-modular Brauer characters.)
gap> mod2:= CharacterTable( "Sz(8)" ) mod 2; BrauerTable( "Sz(8)", 2 ) gap> AutomorphismsOfTable( mod2 ); Group([ (3,4,5)(6,7,8) ]) gap> OrdersClassRepresentatives( mod2 ); [ 1, 5, 7, 7, 7, 13, 13, 13 ]
This means that the first candidate is ruled out; this determines the \(13\)-modular character table of \(2^2.G\).
gap> Length( RepresentativesCharacterTables( cand{ [ 2, 3 ] } ) ); 1 gap> IsRecord( TransformingPermutationsCharacterTables( cand[2], > CharacterTable( "2^2.Sz(8)" ) mod 13 ) ); true
Besides \(2^2.Sz(8)\) (cf. Section 2.7-1), \(2^2.O_8^+(3)\) (cf. Section 2.7-3), and certain central extensions of \(L_3(4)\) (cf. Section 2.7-4), the following examples of central extensions of nearly simple Atlas groups \(G\) by a Klein four group occur.
gap> listV4G:= [ > [ "2^2.L3(4)", "2.L3(4)", "L3(4)" ], > [ "2^2.L3(4).2_1", "2.L3(4).2_1", "L3(4).2_1" ], > [ "(2^2x3).L3(4)", "6.L3(4)", "3.L3(4)" ], > [ "(2^2x3).L3(4).2_1", "6.L3(4).2_1", "3.L3(4).2_1" ], > [ "2^2.O8+(2)", "2.O8+(2)", "O8+(2)" ], > [ "2^2.U6(2)", "2.U6(2)", "U6(2)" ], > [ "(2^2x3).U6(2)", "6.U6(2)", "3.U6(2)" ], > [ "2^2.2E6(2)", "2.2E6(2)", "2E6(2)" ], > [ "(2^2x3).2E6(2)", "6.2E6(2)", "3.2E6(2)" ], > ];;
(For the tables of \((2^2 \times 3).G\), with \(G\) one of \(L_3(4)\), \(U_6(2)\), or \({}^2E_6(2)\), we could alternatively use the tables of \(2^2.G\) and \(3.G\), and the construction described in Chapter 3.)
The function for computing the candidates for the ordinary character tables is similar to the one from Section 2.6-2.
gap> ConstructOrdinaryV4GTable:= function( tblG, tbl2G, name, lib ) > local ord3, nam, poss, reps, trans; > > # Compute the possible actions for the ordinary tables. > ord3:= Set( Filtered( AutomorphismsOfTable( tblG ), > x -> Order( x ) = 3 ), > SmallestGeneratorPerm ); > if 1 < Length( ord3 ) then > Print( "#I ", name, > ": the action of the automorphism is not unique" ); > fi; > # Compute the possible ordinary tables for the given actions. > nam:= Concatenation( "new", name ); > poss:= Concatenation( List( ord3, pi -> > PossibleCharacterTablesOfTypeV4G( tblG, tbl2G, pi, nam ) ) ); > # Test the possibilities for permutation equivalence. > reps:= RepresentativesCharacterTables( poss ); > if 1 < Length( reps ) then > Print( "#I ", name, ": ", Length( reps ), > " equivalence classes\n" ); > elif Length( reps ) = 0 then > Print( "#E ", name, ": no solution\n" ); > else > # Compare the computed table with the library table. > if not IsCharacterTable( lib ) then > Print( "#I no library table for ", name, "\n" ); > PrintToLib( name, poss[1].table ); > else > trans:= TransformingPermutationsCharacterTables( reps[1], lib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " differ\n" ); > fi; > fi; > fi; > return poss; > end;;
Concerning the Brauer tables, the same ambiguity problem may occur as in Section 2.6-2: Some candidates for the ordinary table may be excluded due to information provided by some \(p\)-modular table, see Section 2.7-1 for an easy example. Our strategy is analogous to the one used in Section 2.6-2.
gap> ConstructModularV4GTables:= function( tblG, tbl2G, ordposs, > ordlibtblV4G ) > local name, modposs, primes, checkordinary, i, p, tmodp, 2tmodp, aut, > poss, modlib, trans, reps; > > if not IsCharacterTable( ordlibtblV4G ) then > Print( "#I no ordinary library table ...\n" ); > return []; > fi; > name:= Identifier( ordlibtblV4G ); > modposs:= []; > primes:= ShallowCopy( PrimeDivisors( Size( tblG ) ) ); > ordposs:= ShallowCopy( ordposs ); > checkordinary:= false; > for i in [ 1 .. Length( ordposs ) ] do > modposs[i]:= []; > for p in primes do > tmodp := tblG mod p; > 2tmodp:= tbl2G mod p; > if IsCharacterTable( tmodp ) and IsCharacterTable( 2tmodp ) then > aut:= ConstructionInfoCharacterTable( ordposs[i] )[3]; > poss:= BrauerTableOfTypeV4G( ordposs[i], 2tmodp, aut ); > if CTblLib.Test.TensorDecomposition( poss, false ) = false then > Print( "#I excluded cand. ", i, " (out of ", > Length( ordposs ), ") for ", name, " by ", p, > "-mod. table\n" ); > Unbind( ordposs[i] ); > Unbind( modposs[i] ); > checkordinary:= true; > break; > fi; > Add( modposs[i], poss ); > else > Print( "#I not all input tables for ", name, " mod ", p, > " available\n" ); > primes:= Difference( primes, [ p ] ); > fi; > od; > if IsBound( modposs[i] ) then > # Compare the computed Brauer tables with the library tables. > for poss in modposs[i] do > p:= UnderlyingCharacteristic( poss ); > modlib:= ordlibtblV4G mod p; > if IsCharacterTable( modlib ) then > trans:= TransformingPermutationsCharacterTables( > poss, modlib ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", > name, " mod ", p, " differ\n" ); > fi; > else > Print( "#I no library table for ", > name, " mod ", p, "\n" ); > PrintToLib( name, poss ); > fi; > od; > fi; > od; > if checkordinary then > # Test whether the ordinary table is admissible. > ordposs:= Compacted( ordposs ); > modposs:= Compacted( modposs ); > reps:= RepresentativesCharacterTables( ordposs ); > if 1 < Length( reps ) then > Print( "#I ", name, ": ", Length( reps ), > " equivalence classes (ord. table)\n" ); > elif Length( reps ) = 0 then > Print( "#E ", name, ": no solution (ord. table)\n" ); > else > # Compare the computed table with the library table. > trans:= TransformingPermutationsCharacterTables( reps[1], > ordlibtblV4G ); > if not IsRecord( trans ) then > Print( "#E computed table and library table for ", name, > " differ\n" ); > fi; > fi; > fi; > # Test the uniqueness of the Brauer tables. > for poss in TransposedMat( modposs ) do > reps:= RepresentativesCharacterTables( poss ); > if Length( reps ) <> 1 then > Print( "#I ", name, ": ", Length( reps ), " candidates for the ", > UnderlyingCharacteristic( reps[1] ), "-modular table\n" ); > fi; > od; > return rec( ordinary:= ordposs, modular:= modposs ); > end;;
In our examples, the action of the outer automorphism of order three on the classes of \(G\) turns out to be uniquely determined by the table automorphisms of the character table of \(G\).
gap> for input in listV4G do > tblG := CharacterTable( input[3] ); > tbl2G := CharacterTable( input[2] ); > lib := CharacterTable( input[1] ); > poss := ConstructOrdinaryV4GTable( tblG, tbl2G, input[1], lib ); > ConstructModularV4GTables( tblG, tbl2G, poss, lib ); > od; #I excluded cand. 1 (out of 16) for 2^2.L3(4).2_1 by 7-mod. table #I excluded cand. 2 (out of 16) for 2^2.L3(4).2_1 by 7-mod. table #I excluded cand. 7 (out of 16) for 2^2.L3(4).2_1 by 7-mod. table #I excluded cand. 10 (out of 16) for 2^2.L3(4).2_1 by 7-mod. table #I excluded cand. 15 (out of 16) for 2^2.L3(4).2_1 by 7-mod. table #I excluded cand. 16 (out of 16) for 2^2.L3(4).2_1 by 7-mod. table #I excluded cand. 1 (out of 16) for (2^2x3).L3(4).2_1 by 7-mod. table #I excluded cand. 2 (out of 16) for (2^2x3).L3(4).2_1 by 7-mod. table #I excluded cand. 7 (out of 16) for (2^2x3).L3(4).2_1 by 7-mod. table #I excluded cand. 10 (out of 16) for (2^2x3).L3(4).2_1 by 7-mod. table #I excluded cand. 15 (out of 16) for (2^2x3).L3(4).2_1 by 7-mod. table #I excluded cand. 16 (out of 16) for (2^2x3).L3(4).2_1 by 7-mod. table #I not all input tables for 2^2.2E6(2) mod 2 available #I not all input tables for 2^2.2E6(2) mod 3 available #I not all input tables for 2^2.2E6(2) mod 5 available #I not all input tables for 2^2.2E6(2) mod 7 available #I not all input tables for (2^2x3).2E6(2) mod 2 available #I not all input tables for (2^2x3).2E6(2) mod 3 available #I not all input tables for (2^2x3).2E6(2) mod 5 available #I not all input tables for (2^2x3).2E6(2) mod 7 available #I not all input tables for (2^2x3).2E6(2) mod 11 available #I not all input tables for (2^2x3).2E6(2) mod 13 available #I not all input tables for (2^2x3).2E6(2) mod 17 available #I not all input tables for (2^2x3).2E6(2) mod 19 available
When one tries to construct the character table of the central extensions of \(G = O_8^+(3)\) by a Klein four group, in the same way as in Section 2.7-2, one notices that the order three automorphism that relates the three central extensions of \(G\) by an involution is not uniquely determined.
gap> entry:= [ "2^2.O8+(3)", "2.O8+(3)", "O8+(3)" ];; gap> tblG:= CharacterTable( entry[3] );; gap> aut:= AutomorphismsOfTable( tblG );; gap> ord3:= Set( Filtered( aut, x -> Order( x ) = 3 ), > SmallestGeneratorPerm );; gap> Length( ord3 ); 4
However, the table candidates one gets from the four possible automorphisms turn out to be all equivalent, hence the character table of \(2^2.O_8^+(3)\) can be constructed as follows.
gap> poss:= [];; gap> tbl2G:= CharacterTable( entry[2] ); CharacterTable( "2.O8+(3)" ) gap> for pi in ord3 do > Append( poss, > PossibleCharacterTablesOfTypeV4G( tblG, tbl2G, pi, entry[1] ) ); > od; gap> Length( poss ); 32 gap> poss:= RepresentativesCharacterTables( poss );; gap> Length( poss ); 1
The computed table coincides with the library table.
gap> lib:= CharacterTable( entry[1] );; gap> if TransformingPermutationsCharacterTables( poss[1], lib ) = fail then > Print( "#E differences for ", entry[1], "\n" ); > fi;
The Schur cover of \(G = L_3(4)\) has the structure \((4^2 \times 3).L_3(4)\). Following [CCN+85, p. 23], we regard the multiplier of \(G\) as
\[ M = \langle a, b, c, d \mid [a,b] = [a,c] = [a,d] = [b,c] = [b,d] = [c,d] = a^4 = b^4 = c^4 = d^3 = abc \rangle , \]
and we will consider the automorphism \(\alpha\) of \(M.G\) that acts as \((a,b,c)(d)\) on \(M\).
The subgroup lattice of the subgroup \(\langle a, b, c \rangle = \langle a, b \rangle \cong 4^2\) of \(M\) looks as follows. (The subgroup in the centre of the picture is the Klein four group \(\langle a^2, b^2, c^2 \rangle = \langle a^2, b^2 \rangle\).)
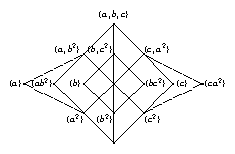
(The symmetry w.r.t. \(\alpha\) would be reflected better in a three dimensional model, with \(\langle a, b \rangle\), \(\langle a^2, b^2 \rangle\), and the trivial subgroup on a vertical symmetry axis, and with the remaining subgroups on three circles such that \(\alpha\) induces a rotation.)
The following is a 3D variant of the picture, which shows the symmetry of order three of the group \(4 \times 4\).
We have \((M / \langle a \rangle).G \cong (M / \langle b \rangle).G \cong (M / \langle c \rangle).G \cong 12_2.G\) and \((M / \langle a b^2 \rangle).G \cong (M / \langle b c^2 \rangle).G \cong (M / \langle c a^2 \rangle).G \cong 12_1.G\). This is because the action of \(G.2_2\) fixes \(a\), and swaps \(b\) and \(c\); so \(b\) is inverted modulo \(\langle a \rangle\) but fixed modulo \(\langle a b^2 \rangle\), and the normal subgroup of order four in \(4_2.G.2_2\) is central but that in \(4_1.G.2_2\) is not central.
The constructions of the character tables of \(4^2.G\) and \((4^2 \times 3).G\) are essentially the same. We start with the table of \(4^2.G\). It can be regarded as a central extension \(H = V.2^2.G\) of \(2^2.G\) by a Klein four group \(V\). The three subgroups of order two in \(V\) are cyclicly permuted by the automorphism of \(M / \langle d \rangle\) induced by \(\alpha\), so the three factors by these subgroups are isomorphic groups \(F\), say, with the structure \((2 \times 4).G\).
The group \(F\) itself is a central extension of \(2.G\) by a Klein four group, but in this case the three factor groups by the order two subgroups of the Klein four group are nonisomorphic groups, of the types \(4_1.G\), \(4_2.G\), and \(2^2.G\), respectively. The GAP function PossibleCharacterTablesOfTypeV4G (CTblLib: PossibleCharacterTablesOfTypeV4G) can be used to construct the character table of \(F\) from the three factors. Note that in this case, no information about table automorphisms is required.
gap> tblG:= CharacterTable( "2.L3(4)" );; gap> tbls2G:= List( [ "4_1.L3(4)", "4_2.L3(4)", "2^2.L3(4)"], > CharacterTable );; gap> poss:= PossibleCharacterTablesOfTypeV4G( tblG, tbls2G, "(2x4).L3(4)" );; gap> Length( poss ); 2 gap> reps:= RepresentativesCharacterTables( poss ); [ CharacterTable( "(2x4).L3(4)" ) ] gap> lib:= CharacterTable( "(2x4).L3(4)" );; gap> IsRecord( TransformingPermutationsCharacterTables( reps[1], lib ) ); true
In the second step, we construct the table of \(4^2.G\) from that of \((2 \times 4).G\) and the table automorphism of \(2^2.G\) that is induced by \(\alpha\); it turns out that the group of table automorphisms of \(2^2.G\) contains a unique subgroup of order three.
gap> tblG:= tbls2G[3]; CharacterTable( "2^2.L3(4)" ) gap> tbl2G:= lib; CharacterTable( "(2x4).L3(4)" ) gap> aut:= AutomorphismsOfTable( tblG );; gap> ord3:= Set( Filtered( aut, x -> Order( x ) = 3 ), > SmallestGeneratorPerm ); [ (2,3,4)(6,7,8)(10,11,12)(13,15,17)(14,16,18)(20,21,22)(24,25,26)(28, 29,30)(32,33,34) ] gap> pi:= ord3[1];; gap> poss:= PossibleCharacterTablesOfTypeV4G( tblG, tbl2G, pi, "4^2.L3(4)" );; gap> Length( poss ); 4 gap> reps:= RepresentativesCharacterTables( poss ); [ CharacterTable( "4^2.L3(4)" ) ] gap> lib:= CharacterTable( "4^2.L3(4)" );; gap> IsRecord( TransformingPermutationsCharacterTables( reps[1], lib ) ); true
With the same approach, we compute the table of \((2 \times 12).G = 2^2.6.G\) from the tables of the three nonisomorphic factor groups \(12_1.G\), \(12_2.G\), and \((2^2 \times 3).G\), and we compute the table of \((4^2 \times 3).G = 2^2.(2^2 \times 3).G\) from the three tables of the factor groups \((2 \times 12).G\) and the action induced by \(\alpha\).
gap> tblG:= CharacterTable( "6.L3(4)" );; gap> tbls2G:= List( [ "12_1.L3(4)", "12_2.L3(4)", "(2^2x3).L3(4)"], > CharacterTable );; gap> poss:= PossibleCharacterTablesOfTypeV4G( tblG, tbls2G, "(2x12).L3(4)" );; gap> Length( poss ); 2 gap> reps:= RepresentativesCharacterTables( poss ); [ CharacterTable( "(2x12).L3(4)" ) ] gap> lib:= CharacterTable( "(2x12).L3(4)" );; gap> IsRecord( TransformingPermutationsCharacterTables( reps[1], lib ) ); true gap> tblG:= CharacterTable( "(2^2x3).L3(4)" ); CharacterTable( "(2^2x3).L3(4)" ) gap> tbl2G:= CharacterTable( "(2x12).L3(4)" ); CharacterTable( "(2x12).L3(4)" ) gap> aut:= AutomorphismsOfTable( tblG );; gap> ord3:= Set( Filtered( aut, x -> Order( x ) = 3 ), > SmallestGeneratorPerm ); [ (2,7,8)(3,4,10)(6,11,12)(14,19,20)(15,16,22)(18,23,24)(26,27,28)(29, 35,41)(30,37,43)(31,39,45)(32,36,42)(33,38,44)(34,40,46)(48,53, 54)(49,50,56)(52,57,58)(60,65,66)(61,62,68)(64,69,70)(72,77, 78)(73,74,80)(76,81,82)(84,89,90)(85,86,92)(88,93,94) ] gap> pi:= ord3[1];; gap> poss:= PossibleCharacterTablesOfTypeV4G( tblG, tbl2G, pi, > "(4^2x3).L3(4)" );; gap> Length( poss ); 4 gap> reps:= RepresentativesCharacterTables( poss ); [ CharacterTable( "(4^2x3).L3(4)" ) ] gap> lib:= CharacterTable( "(4^2x3).L3(4)" );; gap> IsRecord( TransformingPermutationsCharacterTables( reps[1], lib ) ); true
We show an alternative construction of \(p\)-modular tables of certain groups that have been met in Section 2.4-3. Each entry in the GAP list listMGA contains the Identifier (Reference: Identifier for tables of marks) values of character tables of groups of the types \(M.G\), \(G\), \(G.A\), and \(M.G.A\). For each entry with \(|A| = p\), a prime integer, we fetch the \(p\)-modular table of \(G\) and the ordinary table of \(G.A\), compute the action of \(G.A\) on the \(p\)-regular classes of \(G\), and then compute the \(p\)-modular table of \(G.A\). Analogously, we compute the \(p\)-modular table of \(M.G.A\) from the \(p\)-modular table of \(M.G\) and the ordinary table of \(M.G.A\).
gap> for input in listMGA do > ordtblMG := CharacterTable( input[1] ); > ordtblG := CharacterTable( input[2] ); > ordtblGA := CharacterTable( input[3] ); > ordtblMGA := CharacterTable( input[4] ); > p:= Size( ordtblGA ) / Size( ordtblG ); > if IsPrimeInt( p ) then > modtblG:= ordtblG mod p; > if modtblG <> fail then > modtblGA := CharacterTableRegular( ordtblGA, p ); > SetIrr( modtblGA, IBrOfExtensionBySingularAutomorphism( modtblG, > ordtblGA ) ); > modlibtblGA:= ordtblGA mod p; > if modlibtblGA = fail then > Print( "#E ", p, "-modular table of '", Identifier( ordtblGA ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblGA, > modlibtblGA ) = fail then > Print( "#E computed table and library table for ", input[3], > " mod ", p, " differ\n" ); > fi; > fi; > modtblMG:= ordtblMG mod p; > if modtblMG <> fail then > modtblMGA := CharacterTableRegular( ordtblMGA, p ); > SetIrr( modtblMGA, IBrOfExtensionBySingularAutomorphism( modtblMG, > ordtblMGA ) ); > modlibtblMGA:= ordtblMGA mod p; > if modlibtblMGA = fail then > Print( "#E ", p, "-modular table of '", Identifier( ordtblMGA ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblMGA, > modlibtblMGA ) = fail then > Print( "#E computed table and library table for ", input[4], > " mod ", p, " differ\n" ); > fi; > fi; > fi; > od;
We show an alternative construction of \(2\)- and \(3\)-modular tables of certain groups that have been met in Section 2.5-2. Each entry in the GAP list listGS3 contains the Identifier (Reference: Identifier for tables of marks) values of character tables of groups of the types \(G\), \(G.2\), \(G.3\), and \(G.S_3\). For each entry, we fetch the \(2\)-modular table of \(G\) and the ordinary table of \(G.2\), compute the action of \(G.2\) on the \(2\)-regular classes of \(G\), and then compute the \(2\)-modular table of \(G.2\). Analogously, we compute the \(3\)-modular table of \(G.3\) from the \(3\)-modular table of \(G\) and the ordinary table of \(G.3\), and we compute the \(2\)-modular table of \(G.S_3\) from the \(2\)-modular table of \(G.3\) and the ordinary table of \(G.S_3\).
gap> for input in listGS3 do > modtblG:= CharacterTable( input[1] ) mod 2; > if modtblG <> fail then > ordtblG2 := CharacterTable( input[2] ); > modtblG2 := CharacterTableRegular( ordtblG2, 2 ); > SetIrr( modtblG2, IBrOfExtensionBySingularAutomorphism( modtblG, > ordtblG2 ) ); > modlibtblG2:= ordtblG2 mod 2; > if modlibtblG2 = fail then > Print( "#E 2-modular table of '", Identifier( ordtblG2 ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblG2, > modlibtblG2 ) = fail then > Print( "#E computed table and library table for ", input[2], > " mod 2 differ\n" ); > fi; > fi; > modtblG:= CharacterTable( input[1] ) mod 3; > if modtblG <> fail then > ordtblG3 := CharacterTable( input[3] ); > modtblG3 := CharacterTableRegular( ordtblG3, 3 ); > SetIrr( modtblG3, IBrOfExtensionBySingularAutomorphism( modtblG, > ordtblG3 ) ); > modlibtblG3:= ordtblG3 mod 3; > if modlibtblG3 = fail then > Print( "#E 3-modular table of '", Identifier( ordtblG3 ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblG3, > modlibtblG3 ) = fail then > Print( "#E computed table and library table for ", input[3], > " mod 3 differ\n" ); > fi; > fi; > modtblG3:= CharacterTable( input[3] ) mod 2; > if modtblG3 <> fail then > ordtblGS3 := CharacterTable( input[4] ); > modtblGS3 := CharacterTableRegular( ordtblGS3, 2 ); > SetIrr( modtblGS3, IBrOfExtensionBySingularAutomorphism( modtblG3, > ordtblGS3 ) ); > modlibtblGS3:= ordtblGS3 mod 2; > if modlibtblGS3 = fail then > Print( "#E 2-modular table of '", Identifier( ordtblGS3 ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblGS3, > modlibtblGS3 ) = fail then > Print( "#E computed table and library table for ", input[4], > " mod 2 differ\n" ); > fi; > fi; > od;
We show an alternative construction of \(2\)-modular tables of certain groups that have been met in Section 2.6-2. Each entry in the GAP list listGV4 contains the Identifier (Reference: Identifier for tables of marks) values of character tables of groups of the types \(G\), \(G.2_1\), \(G.2_2\), \(G.2_3\), and \(G.2^2\). For each entry, we fetch the \(2\)-modular table of \(G\) and the ordinary tables of the groups \(G.2_i\), and compute the \(2\)-modular tables of \(G.2_i\); Then we compute from this modular table and the ordinary table of \(G.2^2\) the \(2\)-modular table of \(G.2^2\).
gap> for input in listGV4 do > modtblG:= CharacterTable( input[1] ) mod 2; > if modtblG <> fail then > ordtblsG2:= List( input{ [ 2 .. 4 ] }, CharacterTable ); > ordtblGV4:= CharacterTable( input[5] ); > for tblG2 in ordtblsG2 do > modtblG2:= CharacterTableRegular( tblG2, 2 ); > SetIrr( modtblG2, IBrOfExtensionBySingularAutomorphism( modtblG, > tblG2 ) ); > modlibtblG2:= tblG2 mod 2; > if modlibtblG2 = fail then > Print( "#E 2-modular table of '", Identifier( tblG2 ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblG2, > modlibtblG2 ) = fail then > Print( "#E computed table and library table for ", > Identifier( tblG2 ), " mod 2 differ\n" ); > fi; > modtblGV4:= CharacterTableRegular( ordtblGV4, 2 ); > SetIrr( modtblGV4, IBrOfExtensionBySingularAutomorphism( modtblG2, > ordtblGV4 ) ); > modlibtblGV4:= ordtblGV4 mod 2; > if modlibtblGV4 = fail then > Print( "#E 2-modular table of '", Identifier( ordtblGV4 ), > "' is missing\n" ); > elif TransformingPermutationsCharacterTables( modtblGV4, > ordtblGV4 mod 2 ) = fail then > Print( "#E computed table and library table for ", input[5], > " mod 2 differ\n" ); > fi; > od; > fi; > od;
The only example of an Atlas group of the structure \(G.3^3\) is \(U_3(8).3^2\). Its \(3\)-modular character table can be constructed from the known \(3\)-modular character table of any of its index \(3\) subgroups, plus the action of \(U_3(8).3^2\) on the classes of this subgroup.
gap> ordtblG3:= CharacterTable( "U3(8).3^2" );; gap> modlibtblG3:= ordtblG3 mod 3; BrauerTable( "U3(8).3^2", 3 ) gap> for nam in [ "U3(8).3_1", "U3(8).3_2", "U3(8).3_3" ] do > modtblG:= CharacterTable( nam ) mod 3; > if modtblG = fail then > Error( "no 3-modular table of ", nam ); > fi; > modtblG3:= CharacterTableRegular( ordtblG3, 3 ); > SetIrr( modtblG3, IBrOfExtensionBySingularAutomorphism( modtblG, > ordtblG3 ) ); > if TransformingPermutationsCharacterTables( modtblG3, > modlibtblG3 ) = fail then > Print( "#E computed table and library table for ", > Identifier( ordtblG3 ), " mod 3 differ\n" ); > fi; > od;
As expected, we get the same \(3\)-modular table for any choice of the index \(3\) subgroup.
Note that all \(3\)-modular Brauer characters of \(U_3(8).3^2\) lift to characteristic zero.
gap> rest:= RestrictedClassFunctions( Irr( ordtblG3 ), modlibtblG3 );; gap> IsSubset( rest, Irr( modlibtblG3 ) ); true
Typical examples of this construction are those maximal subgroups of alternating groups \(A_n\) that extend in the corresponding symmetric groups \(S_n\) to direct products of the structures \(S_m \times S_{n-m}\), for \(2 < m < n/2\). Also certain subgroups of these maximal subgroups that have this structure can be interesting, see Section 2.4-2.
Also dihedral groups of order \(2 n\) with \(n\) divisible by at least two different primes have the required structure: Let \(n = n_1 n_2\) with coprime \(n_1\), \(n_2\), and let the normal subgroups \(H_1\), \(H_2\) be cyclic subgroups of order \(n_1\) and \(n_2\), respectively, inside the cyclic subgroup of index two. Then the factors \(G/N_1\), \(G/N_2\) are themselves dihedral groups.
So an example (with \(n_1 = 3\) and \(n_2 = 5\)) is the construction of the dihedral group \(D_{30}\) as a subdirect product of index two in the direct product \(D_6 \times D_{10}\).
gap> tblh1:= CharacterTable( "C3" );; gap> tblg1:= CharacterTable( "S3" );; gap> StoreFusion( tblh1, PossibleClassFusions( tblh1, tblg1 )[1], tblg1 ); gap> tblh2:= CharacterTable( "C5" );; gap> tblg2:= CharacterTable( "D10" );; gap> StoreFusion( tblh2, PossibleClassFusions( tblh2, tblg2 )[1], tblg2 ); gap> subdir:= CharacterTableOfIndexTwoSubdirectProduct( tblh1, tblg1, > tblh2, tblg2, "D30" );; gap> IsRecord( TransformingPermutationsCharacterTables( subdir.table, > CharacterTable( "Dihedral", 30 ) ) ); true
The sporadic simple Monster group contains maximal subgroups with the structure \((D_{10} \times HN).2\) (see [CCN+85, p. 234]), the factor group modulo \(D_{10}\) is the automorphism group \(HN.2\) of \(HN\), and the factor group modulo \(HN\) is the Frobenius group \(5:4\) of order \(20\).
gap> tblh1:= CharacterTable( "D10" );; gap> tblg1:= CharacterTable( "5:4" );; gap> tblh2:= CharacterTable( "HN" );; gap> tblg2:= CharacterTable( "HN.2" );; gap> subdir:= CharacterTableOfIndexTwoSubdirectProduct( tblh1, tblg1, > tblh2, tblg2, "(D10xHN).2" );; gap> IsRecord( TransformingPermutationsCharacterTables( subdir.table, > CharacterTable( "(D10xHN).2" ) ) ); true gap> m:= CharacterTable( "M" );; gap> fus:= PossibleClassFusions( subdir.table, m );; gap> Length( fus ); 16 gap> Length( RepresentativesFusions( subdir.table, fus, m ) ); 1
An alternative construction is the one described in Section 2.3-1, as \((D_{10} \times HN).2 = M.G.A\) with \(G = 2 \times HN\), \(M.G = D_{10} \times HN\), and \(G.A\) the subdirect product of \(HN.2\) and a cyclic group of order four (which can be constructed as the isoclinic variant of \(2 \times HN.2\), see Section 2.2-4).
Here is this construction:
gap> c2:= CharacterTable( "C2" );; gap> hn:= CharacterTable( "HN" );; gap> g:= c2 * hn;; gap> d10:= CharacterTable( "D10" );; gap> mg:= d10 * hn;; gap> nsg:= ClassPositionsOfNormalSubgroups( mg ); [ [ 1 ], [ 1, 55 .. 109 ], [ 1, 55 .. 163 ], [ 1 .. 54 ], [ 1 .. 162 ], [ 1 .. 216 ] ] gap> SizesConjugacyClasses( mg ){ nsg[2] }; [ 1, 2, 2 ] gap> g:= mg / nsg[2]; CharacterTable( "D10xHN/[ 1, 55, 109 ]" ) gap> help:= c2 * CharacterTable( "HN.2" ); CharacterTable( "C2xHN.2" ) gap> ga:= CharacterTableIsoclinic( help ); CharacterTable( "Isoclinic(C2xHN.2)" ) gap> gfusga:= PossibleClassFusions( g, ga ); [ [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 23, 24, 25, 25, 26, 27, 28, 29, 30, 31, 32, 32, 33, 33, 34, 35, 36, 37, 37, 38, 39, 40, 40, 41, 42, 42, 43, 43, 44, 44, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 101, 102, 103, 103, 104, 105, 106, 107, 108, 109, 110, 110, 111, 111, 112, 113, 114, 115, 115, 116, 117, 118, 118, 119, 120, 120, 121, 121, 122, 122 ], [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 23, 24, 25, 25, 26, 27, 28, 29, 30, 31, 32, 32, 33, 33, 35, 34, 36, 37, 37, 38, 39, 40, 40, 41, 42, 42, 43, 43, 44, 44, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 101, 102, 103, 103, 104, 105, 106, 107, 108, 109, 110, 110, 111, 111, 113, 112, 114, 115, 115, 116, 117, 118, 118, 119, 120, 120, 121, 121, 122, 122 ] ] gap> StoreFusion( g, gfusga[1], ga ); gap> acts:= PossibleActionsForTypeMGA( mg, g, ga );; gap> Length( acts ); 1 gap> poss:= PossibleCharacterTablesOfTypeMGA( mg, g, ga, acts[1], > "(D10xHN).2" );; gap> Length( poss ); 1 gap> IsRecord( TransformingPermutationsCharacterTables( poss[1].table, > CharacterTable( "(D10xHN).2" ) ) ); true
A group \(G\) is called real if each of its elements is conjugate in \(G\) to its inverse. Equivalently, a group is real if and only if all its character values are real. One might ask whether the Sylow \(2\)-subgroup of a real group is itself real. Counterexamples can be found by a search through GAP's library of small groups. Using the facts we have collected about index two subdirect products in Section 2.3-6, we can demonstrate such a counterexample without using GAP.
Let \(H_1 = A_4\), \(G_1 = S_4\), \(H_2 = C_4\), and \(G_2\) a nonabelian group of order \(8\), and consider the unique index two subgroup \(G\) of \(G_1 \times G_2\) that is different from \(H_1 \times G_2\) and \(G_1 \times H_2\).
Each irreducible character of \(G\) either extends to \(G_1 \times G_2\) or it is induced from an irreducible character of \(H_1 \times H_2\). In the former case, the character is integer valued. Irrational values in the latter case arise as follows.
Let \(\chi\) be an irreducible character of \(H_1 \times H_2\); then it is the product of irreducible characters \(\chi_1\) and \(\chi_2\) of \(H_1\) and \(H_2\), respectively. If \(\chi\) has irrational values then \(\chi_1\) takes primitive third roots of unity \(\omega, \omega^2\) on elements of order three in \(H_1\), or \(\chi_2\) takes primitive fourth roots of unity \(\pm i\) on elements of order four in \(H_2\), or both. In the first two cases, inducing \(\chi\) to \(G\) yields an integer valued character, because each pair of Galois conjugate classes fuses in \(G\) on which \(\chi\) takes irrational values. In the last case, \(\chi\) takes primitive \(12\)-th roots of unity \(\pm i \omega\) and \(\pm i \omega^2\) on elements of order \(12\); since \(G\) fuses the classes with the character values \(i \omega\) and \(-i \omega^2\), we get the character value \(i \omega -i \omega^2 = -\sqrt{{3}}\) in the induced character \(\chi^G\). This means that this character is real valued. Hence \(G\) is real.
Now we consider a Sylow \(2\)-subgroup of \(G\). It has also the structure of a subdirect product, as follows. Let \(H_1 = V_4\), \(G_1 = D_8\), and \(H_2\) and \(G_2\) as above, and consider the unique index two subgroup \(G\) of \(G_1 \times G_2\) that is different from \(H_1 \times G_2\) and \(G_1 \times H_2\).
As above, irrational values in an irreducible character of \(G\) arise only if this character is induced from a character \(\chi\), say, that is the product of irreducible characters \(\chi_1\) and \(\chi_2\) of \(H_1\) and \(H_2\), respectively. In this case, \(\chi_2\) takes primitive fourth roots of unity \(\pm i\) on elements of order four in \(H_2\). Moreover, \(\chi_1\) takes different values \(\pm 1\) on the two classes of \(H_1\) that are fused in \(G\) if the induced character has irrational values, and these values are \(\pm 2i\). Hence the group \(G\) is not real.
(In fact the above two groups of order \(96\) are the smallest real groups with non-real Sylow \(2\)-subgroup, and there are no other such groups of this order.)
generated by GAPDoc2HTML