It is possible to compute the low degree (co)homology of a finite group or monoid of small order directly from the bar resolution. The following commands take this approach to computing the fifth integral homology
\(H_5(Q_4,\mathbb Z) = \mathbb Z_2\oplus\mathbb Z_2\)
of the quaternion group \(G=Q_4\) of order \(8\).
gap> Q:=QuaternionGroup(8);; gap> B:=BarComplexOfMonoid(Q,6);; gap> C:=ContractedComplex(B);; gap> Homology(C,5); [ 2, 2 ] gap> List([0..6],B!.dimension); [ 1, 7, 49, 343, 2401, 16807, 117649 ] gap> List([0..6],C!.dimension); [ 1, 2, 2, 1, 2, 4, 102945 ]
However, this approach is of limited applicability since the bar resolution involves \(|G|^k\) free generators in degree \(k\). A range of techniques, tailored to specific classes of groups, can be used to compute the (co)homology of larger finite groups.
The following example computes the seventh integral homology
\(H_7(M_{23},\mathbb Z) = \mathbb Z_{16}\oplus\mathbb Z_{15}\)
and fourth integral cohomomogy
\(H^4(M_{24},\mathbb Z) = \mathbb Z_{12}\)
of the Mathieu groups \(M_{23}\) and \(M_{24}\). (Warning: the computation of \(H_7(M_{23},\mathbb Z)\) takes a couple of hours to run.)
gap> GroupHomology(MathieuGroup(23),7); [ 16, 3, 5 ] gap> GroupCohomology(MathieuGroup(24),4); [ 4, 3 ]
The following example computes the cokernel
\({\rm coker}( H_3(A_7,\mathbb Z) \rightarrow H_3(S_{10},\mathbb Z)) \cong \mathbb Z_2\oplus \mathbb Z_2\)
of the degree-3 integral homomogy homomorphism induced by the canonical inclusion \(A_7 \rightarrow S_{10}\) of the alternating group on \(7\) letters into the symmetric group on \(10\) letters. The analogous cokernel with \(\mathbb Z_2\) homology coefficients is also computed.
gap> G:=SymmetricGroup(10);; gap> H:=AlternatingGroup(7);; gap> f:=GroupHomomorphismByFunction(H,G,x->x);; gap> F:=GroupHomology(f,3); MappingByFunction( Pcp-group with orders [ 4, 3 ], Pcp-group with orders [ 2, 2, 4, 3 ], function( x ) ... end ) gap> AbelianInvariants(Range(F)/Image(F)); [ 2, 2 ] gap> Fmod2:=GroupHomology(f,3,2);; gap> AbelianInvariants(Range(Fmod2)/Image(Fmod2)); [ 2, 2 ]
The following example computes the third integral homology of the Weyl group \(W=Weyl(E_8)\), a group of order \(696729600\).
\(H_3(Weyl(E_8),\mathbb Z) = \mathbb Z_2 \oplus \mathbb Z_2 \oplus \mathbb Z_{12}\)
gap> L:=SimpleLieAlgebra("E",8,Rationals);; gap> W:=WeylGroup(RootSystem(L));; gap> Order(W); 696729600 gap> GroupHomology(W,3); [ 2, 2, 4, 3 ]
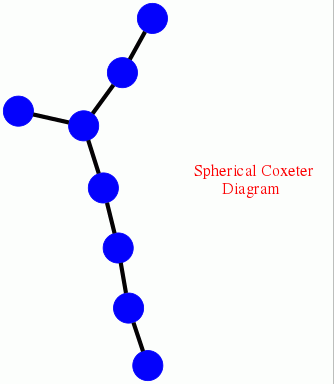
The preceding calculation could be achieved more quickly by noting that \(W=Weyl(E_8)\) is a Coxeter group, and by using the associated Coxeter polytope. The following example uses this approach to compute the fourth integral homology of \(W\). It begins by displaying the Coxeter diagram of \(W\), and then computes
\(H_4(Weyl(E_8),\mathbb Z) = \mathbb Z_2 \oplus \mathbb Z_2 \oplus Z_2 \oplus \mathbb Z_2\).
gap> D:=[[1,[2,3]],[2,[3,3]],[3,[4,3],[5,3]],[5,[6,3]],[6,[7,3]],[7,[8,3]]];; gap> CoxeterDiagramDisplay(D);
gap> polytope:=CoxeterComplex_alt(D,5);; gap> R:=FreeGResolution(polytope,5); Resolution of length 5 in characteristic 0 for <matrix group with 8 generators> . No contracting homotopy available. gap> C:=TensorWithIntegers(R); Chain complex of length 5 in characteristic 0 . gap> Homology(C,4); [ 2, 2, 2, 2 ]
The following example computes the sixth mod-\(2\) homology of the Sylow \(2\)-subgroup \(Syl_2(M_{24})\) of the Mathieu group \(M_{24}\).
\(H_6(Syl_2(M_{24}),\mathbb Z_2) = \mathbb Z_2^{143}\)
gap> GroupHomology(SylowSubgroup(MathieuGroup(24),2),6,2); [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
The following example computes the sixth mod-\(2\) homology of the Unitary group \(U_3(4)\) of order 312000.
\(H_6(U_3(4),\mathbb Z_2) = \mathbb Z_2^{4}\)
gap> G:=GU(3,4);; gap> Order(G); 312000 gap> GroupHomology(G,6,2); [ 2, 2, 2, 2 ]
The following example constructs the Poincare series
\(p(x)=\frac{1}{-x^3+3*x^2-3*x+1}\)
for the cohomology \(H^\ast(Syl_2(M_{12},\mathbb F_2)\). The coefficient of \(x^n\) in the expansion of \(p(x)\) is equal to the dimension of the vector space \(H^n(Syl_2(M_{12},\mathbb F_2)\). The computation involves Singular's Groebner basis algorithms and the Lyndon-Hochschild-Serre spectral sequence.
gap> G:=SylowSubgroup(MathieuGroup(12),2);; gap> P:=PoincareSeriesLHS(G); (1)/(-x_1^3+3*x_1^2-3*x_1+1)
The additional following command uses the Poincare series
gap> RankHomologyPGroup(G,P,1000); 251000
to determine that \(H_{1000}(Syl_2(M_{12},\mathbb Z)\) is a direct sum of 251000 non-trivial cyclic \(2\)-groups.
The following example constructs the series
\(p(x)=\frac{x^4-x^3+x^2-x+1}{x^6-x^5+x^4-2*x^3+x^2-x+1}\)
whose coefficient of \(x^n\) is equal to the dimension of the vector space \(H^n(M_{11},\mathbb F_2)\) for all \(n\) in the range \(0\le n\le 14\). The coefficient is not guaranteed correct for \(n\ge 15\).
gap> PoincareSeriesPrimePart(MathieuGroup(11),2,14); (x_1^4-x_1^3+x_1^2-x_1+1)/(x_1^6-x_1^5+x_1^4-2*x_1^3+x_1^2-x_1+1)
The following example computes
\(H_4(N,\mathbb Z) = \mathbb (Z_3)^4 \oplus \mathbb Z^{84}\)
for the free nilpotent group \(N\) of class \(2\) on four generators.
gap> F:=FreeGroup(4);; N:=NilpotentQuotient(F,2);; gap> GroupHomology(N,4); [ 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
The following example computes
\(H_5(G,\mathbb Z) = \mathbb Z_2 \oplus \mathbb Z_2\)
for the \(3\)-dimensional crystallographic space group \(G\) with Hermann-Mauguin symbol "P62"
gap> GroupHomology(SpaceGroupBBNWZ("P62"),5); [ 2, 2 ]
The following example computes
\(H^5(G,\mathbb Z)= \mathbb Z\)
for an almost crystallographic group.
gap> G:=AlmostCrystallographicPcpGroup( 4, 50, [ 1, -4, 1, 2 ] );; gap> GroupCohomology(G,4); [ 0 ]
The following example computes
\(H_6(SL_2({\cal O},\mathbb Z) = \mathbb Z_2 \oplus \mathbb Z_{12}\)
for \({\cal O}\) the ring of integers of the number field \(\mathbb Q(\sqrt{-2})\).
gap> C:=ContractibleGcomplex("SL(2,O-2)");; gap> R:=FreeGResolution(C,7);; gap> Homology(TensorWithIntegers(R),6); [ 2, 12 ]
The following example computes
\(H_n(G,\mathbb Z) =\left\{ \begin{array}{ll} \mathbb Z &n=0,1,7,8\\ \mathbb Z_2, &n=2,3\\ \mathbb Z_2\oplus \mathbb Z_6, &n=4,6\\ \mathbb Z_3 \oplus \mathbb Z_6,& n=5\\ 0, &n>8 \end{array}\right. \)
for \(G\) the Artin group of type \(E_8\). (Similar commands can be used to compute a resolution and homology of arbitrary Artin monoids and, in thoses cases such as the spherical cases where the \(K(\pi,1)\)-conjecture is known to hold, the homology is equal to that of the corresponding Artin group.)
gap> D:=[[1,[2,3]],[2,[3,3]],[3,[4,3],[5,3]],[5,[6,3]],[6,[7,3]],[7,[8,3]]];; gap> CoxeterDiagramDisplay(D);;
gap> R:=ResolutionArtinGroup(D,9);; gap> C:=TensorWithIntegers(R);; gap> List([0..8],n->Homology(C,n)); [ [ 0 ], [ 0 ], [ 2 ], [ 2 ], [ 2, 6 ], [ 3, 6 ], [ 2, 6 ], [ 0 ], [ 0 ] ]
The Artin group \(G\) projects onto the Coxeter group \(W\) of type \(E_8\). The group \(W\) has a natural representation as a group of \(8\times 8\) integer matrices. This projection gives rise to a representation \(\rho\colon G\rightarrow GL_8(\mathbb Z)\). The following command computes the cohomology group \(H^6(G,\rho) = (\mathbb Z_2)^6\).
gap> G:=R!.group;; gap> gensG:=GeneratorsOfGroup(G);; gap> W:=CoxeterDiagramMatCoxeterGroup(D);; gap> gensW:=GeneratorsOfGroup(W);; gap> rho:=GroupHomomorphismByImages(G,W,gensG,gensW);; gap> C:=HomToIntegralModule(R,rho);; gap> Cohomology(C,6); [ 2, 2, 2, 2, 2, 2 ]
The following example computes
\(H_5(G,\mathbb Z) = \mathbb Z_2\oplus Z_2\oplus Z_2 \oplus Z_2 \oplus Z_2\)
for \(G\) the graph of groups corresponding to the amalgamated product \(G=S_5*_{S_3}S_4\) of the symmetric groups \(S_5\) and \(S_4\) over the canonical subgroup \(S_3\).
gap> S5:=SymmetricGroup(5);SetName(S5,"S5"); gap> S4:=SymmetricGroup(4);SetName(S4,"S4"); gap> A:=SymmetricGroup(3);SetName(A,"S3"); gap> AS5:=GroupHomomorphismByFunction(A,S5,x->x); gap> AS4:=GroupHomomorphismByFunction(A,S4,x->x); gap> D:=[S5,S4,[AS5,AS4]]; gap> GraphOfGroupsDisplay(D);
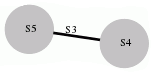
gap> R:=ResolutionGraphOfGroups(D,6);; gap> Homology(TensorWithIntegers(R),5); [ 2, 2, 2, 2, 2 ]
One method of producting a Lie algebra \(L\) from a group \(G\) is by forming the direct sum \(L(G) = G/\gamma_2G \oplus \gamma_2G/\gamma_3G \oplus \gamma_3G/\gamma_4G \oplus \cdots\) of the quotients of the lower central series \(\gamma_1G=G\), \(\gamma_{n+1}G=[\gamma_nG,G]\). Commutation in \(G\) induces a Lie bracket \(L(G)\times L(G) \rightarrow L(G)\).
The homology \(H_n(L)\) of a Lie algebra (with trivial coefficients) can be calculated as the homology of the Chevalley-Eilenberg chain complex \(C_\ast(L)\). This chain complex is implemented in HAP in the cases where the underlying additive group of \(L\) is either finitely generated torsion free or finitely generated of prime exponent \(p\). In these two cases the ground ring for the Lie algebra/ Chevalley-Eilenberg complex is taken to be \(\mathbb Z\) and \(\mathbb Z_p\) respectively.
For example, consider the quotient \(G=F/\gamma_8F\) of the free group \(F=F(x,y)\) on two generators by eighth term of its lower central series. So \(G\) is the free nilpotent group of class 7 on two generators. The following commands compute \(H_4(L(G)) = \mathbb Z_2^{77} \oplus \mathbb Z_6^8 \oplus \mathbb Z_{12}^{51} \oplus \mathbb Z_{132}^{11} \oplus \mathbb Z^{2024}\) and show that the fourth homology in this case contains 2-, 3- and 11-torsion. (The commands take an hour or so to complete.)
gap> G:=Image(NqEpimorphismNilpotentQuotient(FreeGroup(2),7));; gap> L:=LowerCentralSeriesLieAlgebra(G);; gap> h:=LieAlgebraHomology(L,4);; gap> Collected(h); [ [ 0, 2024 ], [ 2, 77 ], [ 6, 8 ], [ 12, 51 ], [ 132, 11 ] ]
For a free nilpotent group \(G\) the additive homology \(H_n(L(G))\) of the Lie algebra can be computed more quickly in HAP than the integral group homology \(H_n(G,\mathbb Z)\). Clearly there are isomorphisms\(H_1(G) \cong H_1(L(G)) \cong G_{ab}\) of abelian groups in homological degree \(n=1\). Hopf's formula can be used to establish an isomorphism \(H_2(G) \cong H_2(L(G))\) also in degree \(n=2\). The following two theorems provide further isomorphisms that allow for the homology of a free nilpotent group to be calculated more efficiently as the homology of the associated Lie algebra.
Theorem 1. [KS98] Let \(G\) be a finitely generated free nilpotent group of class 2. Then the integral group homology \(H_n(G,\mathbb Z)\) is isomorphic to the integral Lie algebra homology \(H_n(L(G),\mathbb Z)\) in each degree \(n\ge0\).
Theorem 2. [IO01] Let \(G\) be a finitely generated free nilpotent group (of any class). Then the integral group homology \(H_n(G,\mathbb Z)\) is isomorphic to the integral Lie algebra homology \(H_n(L(G),\mathbb Z)\) in degrees \(n=0, 1, 2, 3\).
We should remark that experimentation on free nilpotent groups of class \(\ge 4\) has not yielded a group for which the isomorphism \(H_n(G,\mathbb Z) \cong H_n(L(G),\mathbb G)\) fails. For instance, the isomorphism holds in degree \(n=4\) for the free nilpotent group of class 5 on two generators, and for the free nilpotent group of class 2 on four generators:
gap> G:=Image(NqEpimorphismNilpotentQuotient(FreeGroup(2),5));; gap> L:=LowerCentralSeriesLieAlgebra(G);; gap> Collected( LieAlgebraHomology(L,4) ); [ [ 0, 85 ], [ 7, 1 ] ] gap> Collected( GroupHomology(G,4) ); [ [ 0, 85 ], [ 7, 1 ] ] gap> G:=Image(NqEpimorphismNilpotentQuotient(FreeGroup(4),2));; gap> L:=LowerCentralSeriesLieAlgebra(G);; gap> Collected( LieAlgebraHomology(L,4) ); [ [ 0, 84 ], [ 3, 4 ] ] gap> Collected( GroupHomology(G,4) ); [ [ 0, 84 ], [ 3, 4 ] ]
There are various ways to represent a \(\mathbb ZG\)-module \(A\) with action \(G\times A \rightarrow A, (g,a)\mapsto \alpha(g,a)\).
One possibility is to use the data type of a \(G\)-Outer Group which involves three components: an \(ActedGroup\) \(A\); an \(Acting Group\) \(G\); a \(Mapping\) \((g,a)\mapsto \alpha(g,a)\). The following example uses this data type to compute the cohomology \(H^4(G,A) =\mathbb Z_5 \oplus \mathbb Z_{10}\) of the symmetric group \(G=S_6\) with coefficients in the integers \(A=\mathbb Z\) where odd permutations act non-trivially on \(A\).
gap> G:=SymmetricGroup(6);; gap> A:=AbelianPcpGroup([0]);; gap> alpha:=function(g,a); return a^SignPerm(g); end;; gap> A:=GModuleAsGOuterGroup(G,A,alpha); ZG-module with abelian invariants [ 0 ] and G= SymmetricGroup( [ 1 .. 6 ] ) gap> R:=ResolutionFiniteGroup(G,5);; gap> C:=HomToGModule(R,A); G-cocomplex of length 5 . gap> Cohomology(C,4); [ 2, 2, 5 ]
If \(A=\mathbb Z^n\) and \(G\) acts as
\(G\times A \rightarrow A, (g, v) \mapsto \rho(g)\, v \)
where \(\rho\colon G\rightarrow Gl_n(\mathbb Z)\) is a (not necessarily faithful) matrix representation of degree \(n\) then we can avoid the use of \(G\)-outer groups and use just the homomorphism \(\rho\) instead. The following example uses this data type to compute the cohomology
\(H^6(G,A) =\mathbb Z_2 \)
and the homology
\(H_6(G,A) = 0 \)
of the alternating group \(G=A_5\) with coefficients in \(A=\mathbb Z^5\) where elements of \(G\) act on \(\mathbb Z^5\) via an irreducible representation.
gap> G:=AlternatingGroup(5);; gap> rho:=IrreducibleRepresentations(G)[5]; [ (1,2,3,4,5), (3,4,5) ] -> [ [ [ 0, 0, 1, 0, 0 ], [ -1, -1, 0, 0, 1 ], [ 0, 1, 1, 1, 0 ], [ 1, 0, -1, 0, -1 ], [ -1, -1, 0, -1, 0 ] ], [ [ -1, -1, 0, 0, 1 ], [ 1, 0, -1, 0, -1 ], [ 0, 0, 0, 0, 1 ], [ 0, 0, 1, 0, 0 ], [ 0, 0, 0, 1, 0 ] ] ] gap> R:=ResolutionFiniteGroup(G,7);; gap> C:=HomToIntegralModule(R,rho);; gap> Cohomology(C,6); [ 2 ] gap> D:=TensorWithIntegralModule(R,rho); Chain complex of length 7 in characteristic 0 . gap> Homology(D,6); [ ]
If \(V=K^d\) is a vetor space of dimension \(d\) over the field \(K=GF(p)\) with \(p\) a prime and \(G\) acts on \(V\) via a homomorphism \(\rho\colon G\rightarrow GL_d(K)\) then the homology \(H^n(G,V)\) can again be computed without the use of G-outer groups. As an example, the following commands compute
\(H^4(GL(3,2),V) =K^2\)
where \(K=GF(2)\) and \(GL(3,2)\) acts with its natural action on \(V=K^3\).
gap> G:=GL(3,2);; gap> rho:=GroupHomomorphismByFunction(G,G,x->x);; gap> R:=ResolutionFiniteGroup(G,5);; gap> C:=HomToModPModule(R,rho);; gap> Cohomology(C,4); 2
It can be computationally difficult to compute high degree terms in resolutions for large finite groups. But the \(p\)-primary part of the homology can be computed using resolutions of Sylow \(p\)-subgroups. This approach is used in the following example that computes the \(2\)-primary part
\(H_{11}(A_7,A)_{(2)} = \mathbb Z_2 \oplus \mathbb Z_2\oplus \mathbb Z_4\)
of the degree 11 homology of the alternating group \(A_7\) of degree \(7\) with coefficients in the module \(A=\mathbb Z^7\) on which \(A_7\) acts by permuting basis vectors.
gap> G:=AlternatingGroup(7);; gap> rho:=PermToMatrixGroup(G);; gap> R:=ResolutionFiniteGroup(SylowSubgroup(G,2),12);; gap> F:=function(X); return TensorWithIntegralModule(X,rho); end;; gap> PrimePartDerivedFunctor(G,R,F,11); [ 2, 2, 4 ]
Similar commands compute
\(H_{3}(A_{10},A)_{(2)} = \mathbb Z_4\)
with coefficient module \(A=\mathbb Z^{10}\) on which \(A_{10}\) acts by permuting basis vectors.
gap> G:=AlternatingGroup(10);; gap> rho:=PermToMatrixGroup(G);; gap> R:=ResolutionFiniteGroup(SylowSubgroup(G,2),4);; gap> F:=function(X); return TensorWithIntegralModule(X,rho); end;; gap> PrimePartDerivedFunctor(G,R,F,3); [ 4 ]
The following commands compute
\(H_{100}(GL(3,2),V)= K^{34}\)
where \(V\) is the vector space of dimension \(3\) over \(K=GF(2)\) acting via some irreducible representation \(\rho\colon GL(3,2) \rightarrow GL(V)\).
gap> G:=GL(3,2);; gap> rho:=IrreducibleRepresentations(G,GF(2))[3]; CompositionMapping( [ (5,7)(6,8), (2,3,5)(4,7,6) ] -> [ <an immutable 3x3 matrix over GF2>, <an immutable 3x3 matrix over GF2> ], <action isomorphism> ) gap> F:=function(X); return TensorWithModPModule(X,rho); end;; gap> S:=ResolutionPrimePowerGroup(SylowSubgroup(G,2),101);; gap> PrimePartDerivedFunctor(G,S,F,100); [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
Suppose given a group homomorphism \(f\colon G_1\rightarrow G_2\) and a \(G_2\)-module \(A\). Then \(A\) is naturally a \(G_1\)-module with action via \(f\), and there is an induced cohomology homomorphism \(H^n(f,A)\colon H^n(G_2,A) \rightarrow H^n(G_1,A)\).
The following example computes this cohomology homomorphism in degree \(n=6\) for the inclusion \(f\colon A_5 \rightarrow S_5\) and \(A=\mathbb Z^5\) with action that permutes the canonical basis. The final commands determine that the kernel of the homomorphism \(H^6(f,A)\) is the Klein group of order \(4\) and that the cokernel is cyclic of order \(6\).
gap> G1:=AlternatingGroup(5);; gap> G2:=SymmetricGroup(5);; gap> f:=GroupHomomorphismByFunction(G1,G2,x->x);; gap> pi:=PermToMatrixGroup(G2,5);; gap> R1:=ResolutionFiniteGroup(G1,7);; gap> R2:=ResolutionFiniteGroup(G2,7);; gap> F:=EquivariantChainMap(R1,R2,f);; gap> C:=HomToIntegralModule(F,pi);; gap> c:=Cohomology(C,6); [ g1, g2, g3 ] -> [ id, id, g3 ] gap> AbelianInvariants(Kernel(c)); [ 2, 2 ] gap> AbelianInvariants(Range(c)/Image(c)); [ 2, 3 ]
A short exact sequence of \(\mathbb ZG\)-modules \(A \rightarrowtail B \twoheadrightarrow C\) induces a long exact sequence of cohomology groups
\( \rightarrow H^n(G,A) \rightarrow H^n(G,B) \rightarrow H^n(G,C) \rightarrow H^{n+1}(G,A) \rightarrow \) .
Consider the symmetric group \(G=S_4\) and the sequence \( \mathbb Z_4 \rightarrowtail \mathbb Z_8 \twoheadrightarrow \mathbb Z_2\) of trivial \(\mathbb ZG\)-modules. The following commands compute the induced cohomology homomorphism
\(f\colon H^3(S_4,\mathbb Z_4) \rightarrow H^3(S_4,\mathbb Z_8)\)
and determine that the image of this induced homomorphism has order \(8\) and that its kernel has order \(2\).
gap> G:=SymmetricGroup(4);; gap> x:=(1,2,3,4,5,6,7,8);; gap> a:=Group(x^2);; gap> b:=Group(x);; gap> ahomb:=GroupHomomorphismByFunction(a,b,y->y);; gap> A:=TrivialGModuleAsGOuterGroup(G,a);; gap> B:=TrivialGModuleAsGOuterGroup(G,b);; gap> phi:=GOuterGroupHomomorphism();; gap> phi!.Source:=A;; gap> phi!.Target:=B;; gap> phi!.Mapping:=ahomb;; gap> Hphi:=CohomologyHomomorphism(phi,3);; gap> Size(ImageOfGOuterGroupHomomorphism(Hphi)); 8 gap> Size(KernelOfGOuterGroupHomomorphism(Hphi)); 2
The following commands then compute the homomorphism
\(H^3(S_4,\mathbb Z_8) \rightarrow H^3(S_4,\mathbb Z_2)\)
induced by \(\mathbb Z_4 \rightarrowtail \mathbb Z_8 \twoheadrightarrow \mathbb Z_2\), and determine that the kernel of this homomorphsim has order \(8\).
gap> bhomc:=NaturalHomomorphismByNormalSubgroup(b,a); gap> B:=TrivialGModuleAsGOuterGroup(G,b); gap> C:=TrivialGModuleAsGOuterGroup(G,Image(bhomc)); gap> psi:=GOuterGroupHomomorphism(); gap> psi!.Source:=B; gap> psi!.Target:=C; gap> psi!.Mapping:=bhomc; gap> Hpsi:=CohomologyHomomorphism(psi,3); gap> Size(KernelOfGOuterGroupHomomorphism(Hpsi)); 8
The following commands then compute the connecting homomorphism
\(H^2(S_4,\mathbb Z_2) \rightarrow H^3(S_4,\mathbb Z_4)\)
and determine that the image of this homomorphism has order \(2\).
gap> delta:=ConnectingCohomologyHomomorphism(psi,2);; gap> Size(ImageOfGOuterGroupHomomorphism(delta));
Note that the various orders are consistent with exactness of the sequence
\(H^2(S_4,\mathbb Z_2) \rightarrow H^3(S_4,\mathbb Z_4) \rightarrow H^3(S_4,\mathbb Z_8) \rightarrow H^3(S_4,\mathbb Z_2) \) .
Consider the action of the symmetric group \(G=S_5\) on \(A=\mathbb Z^5\) which permutes the canonical basis. The action restricts to the sylow \(2\)-subgroup \(P=Syl_2(G)\). The following commands compute the cohomology transfer homomorphism \(t^4\colon H^4(P,A) \rightarrow H^4(S_5,A)\) and determine its kernel and image. The integral homology transfer \(t_4\colon H_4(S_5,\mathbb Z) \rightarrow H_5(P,\mathbb Z)\) is also computed.
gap> G:=SymmetricGroup(5);; gap> P:=SylowSubgroup(G,2);; gap> R:=ResolutionFiniteGroup(G,5);; gap> A:=PermToMatrixGroup(G);; gap> tr:=TransferCochainMap(R,P,A); Cochain Map between complexes of length 5 . gap> t4:=Cohomology(tr,4); [ g1, g2, g3, g4 ] -> [ id, g1, g2, g4 ] gap> StructureDescription(Kernel(t4)); "C2 x C2" gap> StructureDescription(Image(t4)); "C4 x C2" gap> tr:=TransferChainMap(R,P); Chain Map between complexes of length 5 . gap> Homology(tr,4); [ g1 ] -> [ g1 ]
A spherical 3-manifold is a 3-manifold arising as the quotient \(S^3/\Gamma\) of the 3-sphere \(S^3\) by a finite subgroup \(\Gamma\) of \(SO(4)\) acting freely as rotations. The geometrization conjecture, proved by Grigori Perelman, implies that every closed connected 3-manifold with a finite fundamental group is homeomorphic to a spherical 3-manifold.
A spherical 3-manifold \(S^3/\Gamma\) has finite fundamental group isomorphic to \(\Gamma\). This fundamental group is one of:
\(\Gamma=C_m=\langle x\ |\ x^m\rangle\) (cyclic fundamental group)
\(\Gamma=C_m\times \langle x,y \ |\ xyx^{-1}=y^{-1}, x^{2^k}=y^n \rangle\) for integers \(k, m\ge 1, n\ge 2\) and \(m\) coprime to \(2n\) (prism manifold case)
\(\Gamma= C_m\times \langle x,y, z \ |\ (xy)^2=x^2=y^2, zxz^{-1}=y, zyz^{-1}=xy, z^{3^k}=1\rangle \) for integers \(k,m\ge 1\) and \(m\) coprime to 6 (tetrahedral case)
\(\Gamma=C_m\times\langle x,y\ |\ (xy)^2=x^3=y^4\rangle \) for \(m\ge 1\) coprime to 6 (octahedral case)
\(\Gamma=C_m\times \langle x,y\ |\ (xy)^2=x^3=y^5\rangle \) for \(m\ge 1\) coprime to 30 (icosahedral case).
This list of cases is taken from the Wikipedia pages. The group \(\Gamma\) has periodic cohomology since it acts on a sphere. The cyclic group has period 2 and in the other four cases it has period 4. (Recall that in general a finite group \(G\) has periodic cohomology of period \(n\) if there is an element \(u\in H^n(G,\mathbb Z)\) such that the cup product \(-\ \cup u\colon H^k(G,\mathbb Z) \rightarrow H^{k+n}(G,\mathbb Z)\) is an isomorphism for all \(k\ge 1\). It can be shown that \(G\) has periodic cohomology of period \(n\) if and only if \(H^{n}(G,\mathbb Z)=\mathbb Z_{|G|}\).)
The cohomology of the cyclic group is well-known, and the cohomology of a direct product can be obtained from that of the factors using the Kunneth formula.
In the icosahedral case with \(m=1\) the following commands yield $$H^\ast(\Gamma,\mathbb Z)=Z[t]/(120t=0)$$ with generator \(t\) of degree 4. The final command demonstrates that a periodic resolution is used in the computation.
gap> F:=FreeGroup(2);;x:=F.1;;y:=F.2;; gap> G:=F/[(x*y)^2*x^-3, x^3*y^-5];; gap> Order(G); 120 gap> R:=ResolutionSmallGroup(G,5);; gap> n:=0;;Cohomology(HomToIntegers(R),n); [ 0 ] gap> n:=1;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=2;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=3;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=4;;Cohomology(HomToIntegers(R),n); [ 120 ] gap> List([0..5],k->R!.dimension(k)); [ 1, 2, 2, 1, 1, 2 ]
In the octahedral case with \(m=1\) we obtain $$H^\ast(\Gamma,\mathbb Z) = \mathbb Z[s,t]/(s^2=24t, 2s=0, 48t=0)$$ where \(s\) has degree 2 and \(t\) has degree 4, from the following commands.
gap> F:=FreeGroup(2);;x:=F.1;;y:=F.2;; gap> G:=F/[(x*y)^2*x^-3, x^3*y^-4];; gap> Order(G); 48 gap> R:=ResolutionFiniteGroup(G,5);; gap> n:=0;;Cohomology(HomToIntegers(R),n); [ 0 ] gap> n:=1;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=2;;Cohomology(HomToIntegers(R),n); [ 2 ] gap> n:=3;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=4;;Cohomology(HomToIntegers(R),n); [ 48 ] gap> IntegralCupProduct(R,[1],[1],2,2); [ 24 ]
In the tetrahedral case with \(m=1\) we obtain $$H^\ast(\Gamma,\mathbb Z) = \mathbb Z[s,t]/(s^2=16t, 3s=0, 24t=0)$$ where \(s\) has degree 2 and \(t\) has degree 4, from the following commands.
gap> F:=FreeGroup(3);;x:=F.1;;y:=F.2;;z:=F.3;; gap> G:=F/[(x*y)^2*x^-2, x^2*y^-2, z*x*z^-1*y^-1, z*y*z^-1*y^-1*x^-1,z^3];; gap> Order(G); 24 gap> R:=ResolutionFiniteGroup(G,5);; gap> n:=1;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=2;;Cohomology(HomToIntegers(R),n); [ 3 ] gap> n:=3;;Cohomology(HomToIntegers(R),n); [ ] gap> n:=4;;Cohomology(HomToIntegers(R),n); [ 24 ] gap> IntegralCupProduct(R,[1],[1],2,2); [ 16 ]
A theoretical calculation of the integral and mod-p cohomology rings of all of these fundamental groups of spherical 3-manifolds is given in [TZ08].
Given a \(\mathbb ZG\)-resolution \(R_\ast\) and a \(\mathbb ZG\)-module \(A\), one defines an \(n\)-cocycle to be a \(\mathbb ZG\)-homomorphism \(f\colon R_n \rightarrow A\) for which the composite homomorphism \(fd_{n+1}\colon R_{n+1}\rightarrow A\) is zero. If \(R_\ast\) happens to be the standard bar resolution (i.e. the cellular chain complex of the nerve of the group \(G\) considered as a one object category) then the free \(\mathbb ZG\)-generators of \(R_n\) are indexed by \(n\)-tuples \((g_1 | g_2 | \ldots | g_n)\) of elements \(g_i\) in \(G\). In this case we say that the \(n\)-cocycle is a standard n-cocycle and we think of it as a set-theoretic function
\(f \colon G \times G \times \cdots \times G \longrightarrow A\)
satisfying a certain algebraic cocycle condition. Bearing in mind that a standard \(n\)-cocycle really just assigns an element \(f(g_1, \ldots ,g_n) \in A\) to an \(n\)-simplex in the nerve of \(G\) , the cocycle condition is a very natural one which states that \(f\) must vanish on the boundary of a certain \((n+1)\)-simplex. For \(n=2\) the condition is that a \(2\)-cocycle \(f(g_1,g_2)\) must satisfy
\(g.f(h,k) + f(g,hk) = f(gh,k) + f(g,h)\)
for all \(g,h,k \in G\). This equation is explained by the following picture.
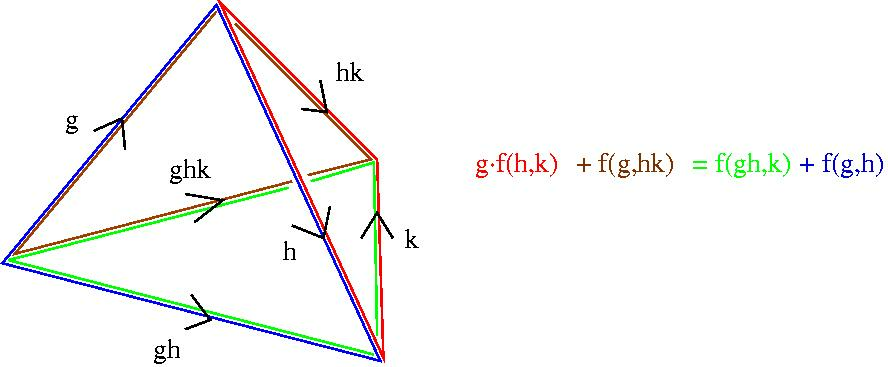
The definition of a cocycle clearly depends on the choice of \(\mathbb ZG\)-resolution \(R_\ast\). However, the cohomology group \(H^n(G,A)\), which is a group of equivalence classes of \(n\)-cocycles, is independent of the choice of \(R_\ast\).
There are some occasions when one needs explicit examples of standard cocycles. For instance:
Let \(G\) be a finite group and \(k\) a field of characteristic \(0\). The group algebra \(k(G)\), and the algebra \(F(G)\) of functions \(d_g\colon G\rightarrow k, h\rightarrow d_{g,h}\), are both Hopf algebras. The tensor product \(F(G) \otimes k(G)\) also admits a Hopf algebra structure known as the quantum double \(D(G)\). A twisted quantum double \(D_f(G)\) was introduced by R. Dijkraaf, V. Pasquier & P. Roche [DPR91]. The twisted double is a quasi-Hopf algebra depending on a \(3\)-cocycle \(f\colon G\times G\times G\rightarrow k\). The multiplication is given by \((d_g \otimes x)(d_h \otimes y) = d_{gx,xh}\beta_g(x,y)(d_g \otimes xy)\) where \(\beta_a \) is defined by \(\beta_a(h,g) = f(a,h,g) f(h,h^{-1}ah,g)^{-1} f(h,g,(hg)^{-1}ahg)\) . Although the algebraic structure of \(D_f(G)\) depends very much on the particular \(3\)-cocycle \(f\), representation-theoretic properties of \(D_f(G)\) depend only on the cohomology class of \(f\).
An explicit \(2\)-cocycle \(f\colon G\times G\rightarrow A\) is needed to construct the multiplication \((a,g)(a',g') = (a + g\cdot a' + f(g,g'), gg')\) in the extension a group \(G\) by a \(\mathbb ZG\)-module \(A\) determined by the cohomology class of \(f\) in \(H^2(G,A)\). See 6.7.
In work on coding theory and Hadamard matrices a number of papers have investigated square matrices \((a_{ij})\) whose entries \(a_{ij}=f(g_i,g_j)\) are the values of a \(2\)-cocycle \(f\colon G\times G \rightarrow \mathbb Z_2\) where \(G\) is a finite group acting trivially on \(\mathbb Z_2\). See for instance [Hor00] and 6.8.
Given a \(\mathbb ZG\)-resolution \(R_\ast\) (with contracting homotopy) and a \(\mathbb ZG\)-module \(A\) one can use HAP commands to compute explicit standard \(n\)-cocycles \(f\colon G^n \rightarrow A\). With the twisted quantum double in mind, we illustrate the computation for \(n=3\), \(G=S_3\), and \(A=U(1)\) the group of complex numbers of modulus \(1\) with trivial \(G\)-action.
We first compute a \(\mathbb ZG\)-resolution \(R_\ast\). The Universal Coefficient Theorem gives an isomorphism \(H_3(G,U(1)) = Hom_{\mathbb Z}(H_3(G,\mathbb Z), U(1))\), The multiplicative group \(U(1)\) can thus be viewed as \(\mathbb Z_m\) where \(m\) is a multiple of the exponent of \(H_3(G,\mathbb Z)\).
gap> G:=SymmetricGroup(3);; gap> R:=ResolutionFiniteGroup(G,4);; gap> TR:=TensorWithIntegers(R);; gap> Homology(TR,3); [ 6 ] gap> R!.dimension(3); 4 gap> R!.dimension(4); 5
We thus replace the very infinite group U(1) by the finite cyclic group \(\mathbb Z_6\). Since the resolution \(R_\ast \) has \(4\) generators in degree \(3\), a homomorphism \(f\colon R^3\rightarrow U(1)\) can be represented by a list \(f=[f_1, f_2, f_3, f_4]\) with \(f_i\) the image in \(\mathbb Z_6\) of the \(i\)th generator. The cocycle condition on \(f\) can be expressed as a matrix equation
\(Mf^t = 0 \bmod 6\).
where the matrix \(M\) is obtained from the following command and \(f^t\) denotes the transpose.
gap> M:=CocycleCondition(R,3);;
A particular cocycle \(f=[f_1, f_2, f_3, f_4]\) can be obtained by choosing a solution to the equation Mf^t=0.
gap> SolutionsMod2:=NullspaceModQ(TransposedMat(M),2); [ [ 0, 0, 0, 0 ], [ 0, 0, 1, 1 ], [ 1, 1, 0, 0 ], [ 1, 1, 1, 1 ] ] gap> SolutionsMod3:=NullspaceModQ(TransposedMat(M),3); [ [ 0, 0, 0, 0 ], [ 0, 0, 0, 1 ], [ 0, 0, 0, 2 ], [ 0, 0, 1, 0 ], [ 0, 0, 1, 1 ], [ 0, 0, 1, 2 ], [ 0, 0, 2, 0 ], [ 0, 0, 2, 1 ], [ 0, 0, 2, 2 ] ]
A non-standard \(3\)-cocycle \(f\) can be converted to a standard one using the command StandardCocycle(R,f,n,q) . This command inputs \( R_\ast\), integers \(n\) and \(q\), and an \(n\)-cocycle \(f\) for the resolution \(R_\ast\). It returns a standard cocycle \(G^n \rightarrow \mathbb Z_q\).
gap> f:=3*SolutionsMod2[3] - SolutionsMod3[5]; #An example solution to Mf=0 mod 6. [ 3, 3, -1, -1 ] gap> Standard_f:=StandardCocycle(R,f,3,6);; gap> g:=Random(G); h:=Random(G); k:=Random(G); (1,2) (1,3,2) (1,3) gap> Standard_f(g,h,k); 3
A function \(f\colon G\times G\times G \rightarrow A\) is a standard \(3\)-cocycle if and only if
\(g\cdot f(h,k,l) - f(gh,k,l) + f(g,hk,l) - f(g,h,kl) + f(g,h,k) = 0\)
for all \(g,h,k,l \in G\). In the above example the group \(G=S_3\) acts trivially on \(A=Z_6\). The following commands show that the standard \(3\)-cocycle produced in the example really does satisfy this \(3\)-cocycle condition.
gap> sf:=Standard_f;; gap> Test:=function(g,h,k,l); > return sf(h,k,l) - sf(g*h,k,l) + sf(g,h*k,l) - sf(g,h,k*l) + sf(g,h,k); > end; function( g, h, k, l ) ... end gap> for g in G do for h in G do for k in G do for l in G do > Print(Test(g,h,k,l),","); > od;od;od;od; 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,6,6,0,0,6, 0,0,0,0,0,6,6,6,0,6,0,12,12,6,12,6,0,12,6,0,6,6,0,0,0,0,0,0,0,12,12,6,6,6,0, 6,6,0,6,6,0,0,-6,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,0,0,0,0,0,0,6,0,0,6,6,0,6,6, 0,6,0,0,6,6,6,0,0,0,0,0,0,0,-6,0,0,-6,0,-6,0,0,0,0,0,0,0,0,6,6,0,6,0,0,6,0,0, 0,0,0,6,6,6,0,0,0,6,6,6,0,0,0,0,-6,0,6,6,0,0,0,0,0,0,0,12,6,6,0,6,0,0,0,0,12, 6,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,0,0,6,0,0,0,0,0,6,6, 6,0,0,0,6,12,6,6,0,0,0,-6,0,0,6,0,0,0,0,0,0,0,12,12,6,6,6,0,0,0,0,6,6,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,0,6,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0, 6,6,0,6,6,0,12,12,6,12,12,0,0,0,0,0,0,0,6,6,0,0,0,0,6,6,6,12,12,0,-6,-6,0,0, 0,0,6,6,0,0,6,0,0,6,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6, 0,6,0,0,6,0,0,0,0,0,0,0,0,0,0,0,6,6,0,6,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,6,0,6,6,0,6,0,0,6,6,6,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,-6,0,6,0,6,0,6,0,0,0,0,0,0,0,12,12,6,12,12,0,6,6,0,6,6,0, 0,0,0,0,0,0,12,12,6,12,12,0,6,6,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0, 0,0,0,0,0,0,6,0,0,6,6,0,6,6,0,6,0,0,6,6,6,0,0,0,-6,0,0,0,-6,0,0,-6,0,-6,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,6,6,0,0,0,0,0,0,0,6,6,0,0,0, 0,0,0,0,6,6,0,-6,0,0,-6,0,0,12,6,0,-6,-6,0,0,0,0,6,6,0,0,6,0,0,6,0,6,6,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,-6,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,6,12,0,6,0,0,6,0,0,0,6,0,0,0,0,0,0, 0,6,12,0,0,0,0,0,0,0,6,6,0,-6,-6,0,0,0,0,0,0,0,0,6,0,0,6,0,6,6,0,0,0,0,0,0,0, 6,0,0,0,6,0,0,6,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6, 0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,6,6,0,6,6,0,6,6,6,12,12,0,0,0,0,0,0,0,6,6,0, 6,6,0,6,6,6,12,12,0,0,0,0,0,0,0,6,6,0,0,6,0,0,6,0,6,6,
Let \(G\) be a finite group with order divisible by prime \(p\). Let \({\mathcal A}={\mathcal A}_p(G)\) denote Quillen's simplicial complex arising as the order complex of the poset of non-trivial elementary abelian \(p\)-subgroups of \(G\). The group \(G\) acts on \(\mathcal A\). Denote the orbit of a \(k\)-simplex \(e^k\) by \([e^k]\), and the stabilizer of \(e^k\) by \(Stab(e^k) \le G\). For a finite abelian group \(H\) let \(H_p\) denote the Sylow \(p\)-subgroup or the "\(p\)-part". Peter Webb proved the following.
Theorem.[Peter Webb] For any \(G\)-module \(M\) there is a (non natural) homomorphism
\(H_n(G,M)_p \oplus \bigoplus_{[e^k]\, :\, k~{\rm odd}~}H_n(Stab(e^k),M)_p \cong \bigoplus_{[e^k]\, : \, k~{\rm even}~}H_n(Stab(e^k),M)_p\)
for \(n\ge 0\). The isomorphism can also be expressed as
\(H_n(G,M)_p \cong \bigoplus_{[e^k]\, : \, k~{\rm even}~}H_n(Stab(e^k),M)_p\ -\ \bigoplus_{[e^k] \, :\, k~{\rm odd}~}H_n(Stab(e^k),M)_p\) and terms can often be cancelled.
Thus the additive structure of the \(p\)-part of the homology of \(G\) is determined by that of the stabilizer groups. The result also holds with homology replaced by cohomology.
Illustration 1
As an illustration of the theorem, the following commands calculate
\(H_n(M_{12},M)_3 \cong \bigoplus_{1\le i\le 3}\,H_n(S_i,M)_3 - \bigoplus_{4\le i\le 5}H_n(S_4,M)_3\)
for the Mathieu simple group \(M_{12}\) of order \(95040\), where
\(S_1\cong S_3=(((C_3 \times C_3) : Q_8) : C_3) : C_2\)
\(S_2=A_4 \times S_3\)
\(S_4=C_3 \times S_3\)
\(S_5=((C_3 \times C_3) : C_3) : (C_2 \times C_2)\) .
gap> G:=MathieuGroup(12);; gap> D:=HomologicalGroupDecomposition(G,3);; gap> List(D[1],StructureDescription); [ "(((C3 x C3) : Q8) : C3) : C2", "A4 x S3", "(((C3 x C3) : Q8) : C3) : C2" ] gap> List(D[2],StructureDescription); [ "C3 x S3", "((C3 x C3) : C3) : (C2 x C2)" ]
Illustration 2
As a second illustration, the following commands show that \(H_n(M_{23},M)_{p}\) is periodic for primes \(p=5, 7, 11, 23\) of periods dividing \(8, 6, 10, 22\) respectively.
gap> G:=MathieuGroup(23);; gap> Factors(Order(G)); [ 2, 2, 2, 2, 2, 2, 2, 3, 3, 5, 7, 11, 23 ] gap> sd:=StructureDescription;; gap> D:=HomologicalGroupDecomposition(G,5);; gap> List(D[1],sd);List(D[2],sd); [ "C15 : C4" ] [ ] gap> IsPeriodic(D[1][1]); true gap> CohomologicalPeriod(D[1][1]); 8 gap> D:=HomologicalGroupDecomposition(G,7);; gap> List(D[1],sd);List(D[2],sd); [ "C2 x (C7 : C3)" ] [ ] gap> IsPeriodic(D[1][1]); true gap> CohomologicalPeriod(D[1][1]); 6 gap> D:=HomologicalGroupDecomposition(G,11);; gap> List(D[1],sd);List(D[2],sd); [ "C11 : C5" ] [ ] gap> IsPeriodic(D[1][1]); true gap> CohomologicalPeriod(D[1][1]); 10 gap> D:=HomologicalGroupDecomposition(G,23);; gap> List(D[1],sd);List(D[2],sd); [ "C23 : C11" ] [ ] gap> IsPeriodic(D[1][1]); true gap> CohomologicalPeriod(D[1][1]); 22
The order \(|M_{23}|=10200960\) is divisible by primes \(p=2, 3, 5, 7, 11, 23\). For \(p=3\) the following commands establish that the Poincare series
\((x^{16} - 2x^{15}\) \( + 3x^{14} - 4x^{13}\) \( + 4x^{12} - 4x^{11}\) \( + 4x^{10} - 3x^9\) \( + 3x^8 - 3x^7 +\) \( 4x^6 - 4x^5 \) \(+ 4x^4 -4x^3\) \( + 3x^2 -2x + 1) /\) \( (x^{18} - 2x^{17}\) \( + 3x^{16} - 4x^{15}\) \( + 4x^{14} - \) \(4x^{13} + 4x^{12}\) \( - 4x^{11} + 4x^{10}\) \( - 4x^9 + 4x^8\) \( - 4x^7 + 4x^6 \) \( - 4x^5 + 4x^4\) \( - 4x^3 +\) \( 3x^2 - 2x + 1)\)
describes the dimension of the vector space \(H^n(M_{23},\mathbb Z_3)\) up to at least degree \(n=40\). To prove that it describes the dimension in all degrees one would need to verify "completion criteria".
gap> G:=MathieuGroup(23);; gap> D:=HomologicalGroupDecomposition(G,3);; gap> List(D[1],StructureDescription); [ "(C3 x C3) : QD16", "A5 : S3" ] gap> List(D[2],StructureDescription); [ "S3 x S3" ] gap> P1:=PoincareSeriesPrimePart(D[1][1],3,40); (x_1^16-2*x_1^15+3*x_1^14-4*x_1^13+4*x_1^12-4*x_1^11+4*x_1^10-3*x_1^9+3*x_1^8-3*x_1^7+4*x_1^6-4*x_1^5+\ 4*x_1^4-4*x_1^3+3*x_1^2-2*x_1+1)/(x_1^18-2*x_1^17+3*x_1^16-4*x_1^15+4*x_1^14-4*x_1^13+4*x_1^12-4*x_1^1\ 1+4*x_1^10-4*x_1^9+4*x_1^8-4*x_1^7+4*x_1^6-4*x_1^5+4*x_1^4-4*x_1^3+3*x_1^2-2*x_1+1) gap> P2:=PoincareSeriesPrimePart(D[1][2],3,40); (x_1^4-2*x_1^3+3*x_1^2-2*x_1+1)/(x_1^6-2*x_1^5+3*x_1^4-4*x_1^3+3*x_1^2-2*x_1+1) gap> P3:=PoincareSeriesPrimePart(D[2][1],3,40); (x_1^4-2*x_1^3+3*x_1^2-2*x_1+1)/(x_1^6-2*x_1^5+3*x_1^4-4*x_1^3+3*x_1^2-2*x_1+1)
Let \(A\) be the Lie algebra constructed from the associative algebra \(M^{4\times 4}(\mathbb Q)\) of all \(4\times 4\) rational matrices. Let \(V\) be its adjoint module (with underlying vector space of dimension \(16\) and equal to that of \(A\)). The following commands compute \(H_{4}(A,V) = \mathbb Q\).
gap> M:=FullMatrixAlgebra(Rationals,4);; gap> A:=LieAlgebra(M);; gap> V:=AdjointModule(A);; gap> C:=ChevalleyEilenbergComplex(V,17);; gap> List([0..17],C!.dimension); [ 16, 256, 1920, 8960, 29120, 69888, 128128, 183040, 205920, 183040, 128128, 69888, 29120, 8960, 1920, 256, 16, 0 ] gap> Homology(C,4); 1
Note that the eighth term \(C_{8}(V)\) in the Chevalley-Eilenberg complex \(C_\ast(V)\) is a vector space of dimension \(205920\) and so it will take longer to compute the homology in degree \(8\).
As a second example, let \(B\) be the classical Lie ring of type \(B_3\) over the ring of integers. The following commands compute \(H_3(B,\mathbb Z)= \mathbb Z \oplus \mathbb Z_2^{105}\).
gap> A:=SimpleLieAlgebra("B",7,Integers); <Lie algebra of dimension 105 over Integers> gap> C:=ChevalleyEilenbergComplex(A,4,"sparse"); Sparse chain complex of length 4 in characteristic 0 . gap> D:=ContractedComplex(C); Sparse chain complex of length 4 in characteristic 0 . gap> Collected(Homology(D,3)); [ [ 0, 1 ], [ 2, 105 ] ]
A short exact sequence of Lie algebras
\( M \rightarrowtail C \twoheadrightarrow L \)
(over a field \(k\)) is said to be a stem extension of \(L\) if \(M\) lies both in the centre \(Z(C)\) and in the derived subalgeba \(C^2\). If, in addition, the rank of the vector space \(M\) is equal to the rank of the second Chevalley-Eilenberg homology \(H_2(L,k)\) then the Lie algebra \(C\) is said to be a cover of \(L\).
Each finite dimensional Lie algebra \(L\) admits a cover \(C\), and this cover can be shown to be unique up to Lie isomorphism.
The cover can be used to determine whether there exists a Lie algebra \(E\) whose central quotient \(E/Z(E)\) is isomorphic to \(L\). The image in \(L\) of the centre of \(C\) is called the Lie Epicentre of \(L\), and this image is trivial if and only if such an \(E\) exists.
The cover can also be used to determine the stem extensions of \(L\). It can be shown that each stem extension is a quotient of the cover by an ideal in the Lie multiplier \(H_2(L,k)\).
The following commands compute the cover \(C\) of the solvable but non-nilpotent 13-dimensional Lie algebra \(L\) (over \(k=\mathbb Q\)) that was introduced by M. Wuestner [Wue92]. They also show that: the second homology of \(C\) is trivial and compute the ranks of the homology groups in other dimensions; the Lie algebra \(L\) is not isomorphic to any central quotient \(E/Z(E)\).
gap> SCTL:=EmptySCTable(13,0,"antisymmetric");; gap> SetEntrySCTable( SCTL, 1, 6, [ 1, 7 ] );; gap> SetEntrySCTable( SCTL, 1, 8, [ 1, 9 ] );; gap> SetEntrySCTable( SCTL, 1, 10, [ 1, 11 ] );; gap> SetEntrySCTable( SCTL, 1, 12, [ 1, 13 ] );; gap> SetEntrySCTable( SCTL, 1, 7, [ -1, 6 ] );; gap> SetEntrySCTable( SCTL, 1, 9, [ -1, 8 ] );; gap> SetEntrySCTable( SCTL, 1, 11, [ -1, 10 ] );; gap> SetEntrySCTable( SCTL, 1, 13, [ -1, 12 ] );; gap> SetEntrySCTable( SCTL, 6, 7, [ 1, 2 ] );; gap> SetEntrySCTable( SCTL, 8, 9, [ 1, 3 ] );; gap> SetEntrySCTable( SCTL, 6, 9, [ -1, 5 ] );; gap> SetEntrySCTable( SCTL, 7, 8, [ 1, 5 ] );; gap> SetEntrySCTable( SCTL, 2, 8, [ 1, 12 ] );; gap> SetEntrySCTable( SCTL, 2, 9, [ 1, 13 ] );; gap> SetEntrySCTable( SCTL, 3, 6, [ 1, 10 ] );; gap> SetEntrySCTable( SCTL, 3, 7, [ 1, 11 ] );; gap> SetEntrySCTable( SCTL, 2, 3, [ 1, 4 ] );; gap> SetEntrySCTable( SCTL, 5, 6, [ -1, 12 ] );; gap> SetEntrySCTable( SCTL, 5, 7, [ -1, 13 ] );; gap> SetEntrySCTable( SCTL, 5, 8, [ -1, 10 ] );; gap> SetEntrySCTable( SCTL, 5, 9, [ -1, 11 ] );; gap> SetEntrySCTable( SCTL, 6, 11, [ -1/2, 4 ] );; gap> SetEntrySCTable( SCTL, 7, 10, [ 1/2, 4 ] );; gap> SetEntrySCTable( SCTL, 8, 13, [ 1/2, 4 ] );; gap> SetEntrySCTable( SCTL, 9, 12, [ -1/2, 4 ] );; gap> L:=LieAlgebraByStructureConstants(Rationals,SCTL);; gap> C:=Source(LieCoveringHomomorphism(L)); <Lie algebra of dimension 15 over Rationals> gap> Dimension(LieEpiCentre(L)); 1 gap> ch:=ChevalleyEilenbergComplex(C,17);; gap> List([0..16],n->Homology(ch,n)); [ 1, 1, 0, 9, 23, 27, 47, 88, 88, 47, 27, 23, 9, 0, 1, 1, 0 ]
generated by GAPDoc2HTML