accumulated coefficients)
This chapter contains the basic definitions, and it describes how to enter residue-class-wise affine mappings and how to compute with them.
How to compute with residue-class-wise affine groups is described in detail in the next chapter. The reader is encouraged to look there already after having read the first few pages of this chapter, and to look up definitions as he needs to.
Residue-class-wise affine groups, or rcwa groups for short, are permutation groups whose elements are bijective residue-class-wise affine mappings.
A mapping \(f: ℤ \rightarrow ℤ\) is called residue-class-wise affine, or for short an rcwa mapping, if there is a positive integer \(m\) such that the restrictions of \(f\) to the residue classes \(r(m) \in ℤ/mℤ\) are all affine, i.e. given by
for certain coefficients \(a_{r(m)}, b_{r(m)}, c_{r(m)} \in ℤ\) depending on \(r(m)\). The smallest possible \(m\) is called the modulus of \(f\). It is understood that all fractions are reduced, i.e. that \(\gcd( a_{r(m)}, b_{r(m)}, c_{r(m)} ) = 1\), and that \(c_{r(m)} > 0\). The lcm of the coefficients \(a_{r(m)}\) is called the multiplier of \(f\), and the lcm of the coefficients \(c_{r(m)}\) is called the divisor of \(f\).
It is easy to see that the residue-class-wise affine mappings of ℤ form a monoid under composition, and that the residue-class-wise affine permutations of ℤ form a countable subgroup of Sym(ℤ). We denote the former by Rcwa(ℤ), and the latter by RCWA(ℤ).
An rcwa mapping is called tame if the set of moduli of its powers is bounded, or equivalently if it permutes a partition of ℤ into finitely many residue classes on all of which it is affine. An rcwa group is called tame if there is a common such partition for all of its elements, or equivalently if the set of moduli of its elements is bounded. Rcwa mappings and -groups which are not tame are called wild. Tame rcwa mappings and -groups are something which one could call the trivial cases
or basic building blocks
, while wild rcwa groups are the objects of primary interest.
The definitions of residue-class-wise affine mappings and -groups can be generalized in the obvious way to suitable rings other than ℤ. In fact, this package provides also some support for residue-class-wise affine groups over \(ℤ^2\), over semilocalizations of ℤ and over univariate polynomial rings over finite fields. The ring \(ℤ^2\) has been chosen as an example of a suitable ring which is not a principal ideal domain, the semilocalizations of ℤ have been chosen as examples of rings with only finitely many prime elements, and the univariate polynomial rings over finite fields have been chosen as examples of rings with nonzero characteristic.
Entering an rcwa mapping of ℤ requires giving the modulus \(m\) and the coefficients \(a_{r(m)}\), \(b_{r(m)}\) and \(c_{r(m)}\) for \(r(m)\) running over the residue classes (mod \(m\)).
This can be done easiest by RcwaMapping( coeffs ), where coeffs is a list of \(m\) coefficient triples coeffs[\(r+1\)] = [\(a_{r(m)}\), \(b_{r(m)}\), \(c_{r(m)}\)], with \(r\) running from 0 to \(m-1\).
If some coefficient \(c_{r(m)}\) is zero or if images of some integers under the mapping to be defined would not be integers, an error message is printed and a break loop is entered. For example, the coefficient triple [1,4,3] is not allowed at the first position. The reason for this is that not all integers congruent to \(1 \cdot 0 + 4 = 4\) mod \(m\) are divisible by 3.
For the general constructor for rcwa mappings, see RcwaMapping (2.2-5).
gap> T := RcwaMapping([[1,0,2],[3,1,2]]); # The Collatz mapping. <rcwa mapping of Z with modulus 2> gap> [ IsSurjective(T), IsInjective(T) ]; [ true, false ] gap> Display(T); Surjective rcwa mapping of Z with modulus 2 / | n/2 if n in 0(2) n |-> < (3n+1)/2 if n in 1(2) | \ gap> a := RcwaMapping([[2,0,3],[4,-1,3],[4,1,3]]); <rcwa mapping of Z with modulus 3> gap> IsBijective(a); true gap> Display(a); # This is Collatz' permutation: Rcwa permutation of Z with modulus 3 / | 2n/3 if n in 0(3) n |-> < (4n-1)/3 if n in 1(3) | (4n+1)/3 if n in 2(3) \ gap> Support(a); Z \ [ -1, 0, 1 ] gap> Cycle(a,44); [ 44, 59, 79, 105, 70, 93, 62, 83, 111, 74, 99, 66 ]
There is computational evidence for the conjecture that any residue-class-wise affine permutation of ℤ can be factored into members of the following three series of permutations of particularly simple structure (cf. FactorizationIntoCSCRCT (2.5-2)):
‣ ClassShift( r, m ) | ( function ) |
‣ ClassShift( cl ) | ( function ) |
Returns: the class shift \(\nu_{r(m)}\).
The class shift \(\nu_{r(m)}\) is the rcwa mapping of ℤ which maps \(n \in r(m)\) to \(n + m\) and which fixes \(ℤ \setminus r(m)\) pointwise.
In the one-argument form, the argument cl stands for the residue class \(r(m)\). Enclosing the argument list in list brackets is permitted.
gap> Display(ClassShift(5,12)); Tame rcwa permutation of Z with modulus 12, of order infinity / | n+12 if n in 5(12) n |-> < n if n in Z \ 5(12) | \
‣ ClassReflection( r, m ) | ( function ) |
‣ ClassReflection( cl ) | ( function ) |
Returns: the class reflection \(\varsigma_{r(m)}\).
The class reflection \(\varsigma_{r(m)}\) is the rcwa mapping of ℤ which maps \(n \in r(m)\) to \(-n + 2r\) and which fixes \(ℤ \setminus r(m)\) pointwise, where it is understood that \(0 \leq r < m\).
In the one-argument form, the argument cl stands for the residue class \(r(m)\). Enclosing the argument list in list brackets is permitted.
gap> Display(ClassReflection(5,9)); Rcwa permutation of Z with modulus 9, of order 2 / | -n+10 if n in 5(9) n |-> < n if n in Z \ 5(9) | \
‣ ClassTransposition( r1, m1, r2, m2 ) | ( function ) |
‣ ClassTransposition( cl1, cl2 ) | ( function ) |
Returns: the class transposition \(\tau_{r_1(m_1),r_2(m_2)}\).
Given two disjoint residue classes \(r_1(m_1)\) and \(r_2(m_2)\) of the integers, the class transposition \(\tau_{r_1(m_1),r_2(m_2)}\) \(\in\) RCWA(ℤ) is defined as the involution which interchanges \(r_1+km_1\) and \(r_2+km_2\) for any integer \(k\) and which fixes all other points. It is understood that \(m_1\) and \(m_2\) are positive, that \(0 \leq r_1 < m_1\) and that \(0 \leq r_2 < m_2\). For a generalized class transposition, the latter assumptions are not made.
The class transposition \(\tau_{r_1(m_1),r_2(m_2)}\) interchanges the residue classes \(r_1(m_1)\) and \(r_2(m_2)\) and fixes the complement of their union pointwise.
In the four-argument form, the arguments r1, m1, r2 and m2 stand for \(r_1\), \(m_1\), \(r_2\) and \(m_2\), respectively. In the two-argument form, the arguments cl1 and cl2 stand for the residue classes \(r_1(m_1)\) and \(r_2(m_2)\), respectively. Enclosing the argument list in list brackets is permitted. The residue classes \(r_1(m_1)\) and \(r_2(m_2)\) are stored as an attribute TransposedClasses.
A list of all class transpositions interchanging residue classes with moduli less than or equal to a given bound m can be obtained by List(ClassPairs([P],m),ClassTransposition), where the function ClassPairs returns a list of all 4-tuples \((r_1,m_1,r_2,m_2)\) of integers corresponding to the unordered pairs of disjoint residue classes \(r_1(m_1)\) and \(r_2(m_2)\) with \(m_1\) and \(m_2\) less than or equal to the specified bound. If a list of primes is given as optional argument P, then the returned list contains only those 4-tuples where all prime factors of \(m_1\) and \(m_2\) lie in P. If the option divisors is set, the returned list contains only the 4-tuples where \(m_1\) and \(m_2\) divide m.
The function NrClassPairs(m) returns the length of the list ClassPairs(m), where the result is computed much faster and without actually generating the list of tuples. Given a class transposition ct, the corresponding 4-tuple can be obtained by ExtRepOfObj(ct)
A class transposition can be written as a product of any given number \(k\) of class transpositions. Such a decomposition can be obtained by SplittedClassTransposition(ct,k).
gap> Display(ClassTransposition(1,2,8,10):CycleNotation:=false); Rcwa permutation of Z with modulus 10, of order 2 / | 5n+3 if n in 1(2) n |-> < (n-3)/5 if n in 8(10) | n if n in 0(2) \ 8(10) \ gap> List(ClassPairs(4),ClassTransposition); [ ( 0(2), 1(2) ), ( 0(2), 1(4) ), ( 0(2), 3(4) ), ( 0(3), 1(3) ), ( 0(3), 2(3) ), ( 0(4), 1(4) ), ( 0(4), 2(4) ), ( 0(4), 3(4) ), ( 1(2), 0(4) ), ( 1(2), 2(4) ), ( 1(3), 2(3) ), ( 1(4), 2(4) ), ( 1(4), 3(4) ), ( 2(4), 3(4) ) ] gap> NrClassPairs(100); 3528138 gap> SplittedClassTransposition(ClassTransposition(0,2,1,4),3); [ ( 0(6), 1(12) ), ( 2(6), 5(12) ), ( 4(6), 9(12) ) ]
The set of all class transpositions of the ring of integers generates the simple group CT(ℤ) mentioned in Chapter 1. This group has a representation as a GAP object -- see CT (3.1-9). The set of all generalized class transpositions of ℤ generates a simple group as well, cf. [Koh10].
Class shifts, class reflections and class transpositions of rings \(R\) other than ℤ are defined in an entirely analogous way -- all one needs to do is to replace ℤ by \(R\) and to read \(<\) and \(\leq\) in the sense of the ordering used by GAP. They can also be entered basically as described above -- just prepend the desired ring \(R\) to the argument list. Often also a sensible default ring
(\(\rightarrow\) DefaultRing in the GAP Reference Manual) is chosen if that optional first argument is omitted.
On rings which have more than two units, there is another basic series of rcwa permutations which generalizes class reflections:
‣ ClassRotation( r, m, u ) | ( function ) |
‣ ClassRotation( cl, u ) | ( function ) |
Returns: the class rotation \(\rho_{r(m),u}\).
Given a residue class \(r(m)\) and a unit \(u\) of a suitable ring \(R\), the class rotation \(\rho_{r(m),u}\) is the rcwa mapping which maps \(n \in r(m)\) to \(un + (1-u)r\) and which fixes \(R \setminus r(m)\) pointwise. Class rotations generalize class reflections, as we have \(\rho_{r(m),-1} = \varsigma_{r(m)}\).
In the two-argument form, the argument cl stands for the residue class \(r(m)\). Enclosing the argument list in list brackets is permitted. The argument u is stored as an attribute RotationFactor.
gap> Display(ClassRotation(ResidueClass(Z_pi(2),2,1),1/3)); Tame rcwa permutation of Z_( 2 ) with modulus 2, of order infinity / | 1/3 n + 2/3 if n in 1(2) n |-> < n if n in 0(2) | \ gap> x := Indeterminate(GF(8),1);; SetName(x,"x"); gap> R := PolynomialRing(GF(8),1);; gap> cr := ClassRotation(1,x,Z(8)*One(R)); Support(cr); ClassRotation( 1(x), Z(2^3) ) 1(x) \ [ 1 ] gap> Display(cr); Rcwa permutation of GF(2^3)[x] with modulus x, of order 7 / | Z(2^3)*P + Z(2^3)^3 if P in 1(x) P |-> < P otherwise | \
IsClassShift, IsClassReflection, IsClassRotation, IsClassTransposition and IsGeneralizedClassTransposition are properties which indicate whether a given rcwa mapping belongs to the corresponding series.
In the sequel we describe the general-purpose constructor for rcwa mappings. The constructor may look a bit technical on a first glance, but knowing all possible ways of entering an rcwa mapping is by no means necessary for understanding this manual or for using this package.
‣ RcwaMapping( R, m, coeffs ) | ( method ) |
‣ RcwaMapping( R, coeffs ) | ( method ) |
‣ RcwaMapping( coeffs ) | ( method ) |
‣ RcwaMapping( perm, range ) | ( method ) |
‣ RcwaMapping( m, values ) | ( method ) |
‣ RcwaMapping( pi, coeffs ) | ( method ) |
‣ RcwaMapping( q, m, coeffs ) | ( method ) |
‣ RcwaMapping( P1, P2 ) | ( method ) |
‣ RcwaMapping( cycles ) | ( method ) |
‣ RcwaMapping( expression ) | ( method ) |
Returns: an rcwa mapping.
In all cases the argument R is the underlying ring, m is the modulus and coeffs is the coefficient list. A coefficient list for an rcwa mapping with modulus \(m\) consists of \(|R/mR|\) coefficient triples [\(a_{r(m)}\), \(b_{r(m)}\), \(c_{r(m)}\)]. Their ordering is determined by the ordering of the representatives of the residue classes (mod \(m\)) in the sorted list returned by AllResidues(R, m). In case \(R = ℤ\) this means that the coefficient triple for the residue class \(0(m)\) comes first and is followed by the one for \(1(m)\), the one for \(2(m)\) and so on.
If one or several of the arguments R, m and coeffs are omitted or replaced by other arguments, the former are either derived from the latter or default values are chosen. The meaning of the other arguments is defined in the detailed description of the particular methods given in the sequel. The above methods return the rcwa mapping
of R with modulus m and coefficients coeffs,
of R = ℤ or R = \(ℤ_{(\pi)}\) with modulus Length(coeffs) and coefficients coeffs,
of R = ℤ with modulus Length(coeffs) and coefficients coeffs,
of R = ℤ, permuting any set range+k*Length(range) like perm permutes range,
of R = ℤ with modulus m and values given by a list val of 2 pairs [preimage, image] per residue class (mod m),
of R = \(ℤ_{(\pi)}\) with modulus Length(coeffs) and coefficients coeffs (the set of primes \(\pi\) which denotes the underlying ring is passed as argument pi),
of R = GF(q)[x] with modulus m and coefficients coeffs,
an rcwa permutation which induces a bijection between the partitions P1 and P2 of R into residue classes and which is affine on the elements of P1,
an rcwa permutation with residue class cycles
given by a list cycles of lists of pairwise disjoint residue classes, each of which it permutes cyclically, or
the rcwa permutation of ℤ given by the arithmetical expression expression -- a string consisting of class transpositions (e.g. "(0(2),1(4))") or cycles permuting residue classes (e.g. "(0(2),1(8),3(4),5(8))"), class shifts (e.g. "cs(4(6))", class reflections (e.g. "cr(3(4))"), arithmetical operators ("*", "/" and "^") and brackets ("(", ")"),
respectively. The methods for the operation RcwaMapping perform a number of argument checks, which can be skipped by using RcwaMappingNC instead.
gap> R := PolynomialRing(GF(2),1);; x := X(GF(2),1);; SetName(x,"x"); gap> RcwaMapping(R,x+1,[[1,0,x+One(R)],[x+One(R),0,1]]*One(R)); # (a) <rcwa mapping of GF(2)[x] with modulus x+1> gap> RcwaMapping(Z_pi(2),[[1/3,0,1]]); # (b) Rcwa mapping of Z_( 2 ): n -> 1/3 n gap> a := RcwaMapping([[2,0,3],[4,-1,3],[4,1,3]]); # (c) <rcwa mapping of Z with modulus 3> gap> RcwaMapping((1,2,3),[1..4]); # (d) ( 1(4), 2(4), 3(4) ) gap> T = RcwaMapping(2,[[1,2],[2,1],[3,5],[4,2]]); # (e) true gap> RcwaMapping([2],[[1/3,0,1]]); # (f) Rcwa mapping of Z_( 2 ): n -> 1/3 n gap> RcwaMapping(2,x+1,[[1,0,x+One(R)],[x+One(R),0,1]]*One(R)); # (g) <rcwa mapping of GF(2)[x] with modulus x+1> gap> a = RcwaMapping(List([[0,3],[1,3],[2,3]],ResidueClass), > List([[0,2],[1,4],[3,4]],ResidueClass)); # (h) true gap> RcwaMapping([List([[0,2],[1,4],[3,8],[7,16]],ResidueClass)]); # (i) ( 0(2), 1(4), 3(8), 7(16) ) gap> Cycle(last,ResidueClass(0,2)); [ 0(2), 1(4), 3(8), 7(16) ] gap> g := RcwaMapping("((0(4),1(6))*cr(0(6)))^2/cs(2(8))"); # (j) <rcwa permutation of Z with modulus 72> gap> g = (ClassTransposition(0,4,1,6) * ClassReflection(0,6))^2/ > ClassShift(2,8); true
Rcwa mappings of ℤ can be translated
to rcwa mappings of some semilocalization \(ℤ_{(\pi)}\) of ℤ:
‣ LocalizedRcwaMapping( f, p ) | ( function ) |
‣ SemilocalizedRcwaMapping( f, pi ) | ( function ) |
Returns: the rcwa mapping of \(ℤ_{(p)}\) respectively \(ℤ_{(\pi)}\) with the same coefficients as the rcwa mapping f of ℤ.
The argument p or pi must be a prime or a set of primes, respectively. The argument f must be an rcwa mapping of ℤ whose modulus is a power of p, or whose modulus has only prime divisors which lie in pi, respectively.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> Cycle(LocalizedRcwaMapping(T,2),131/13); [ 131/13, 203/13, 311/13, 473/13, 716/13, 358/13, 179/13, 275/13, 419/13, 635/13, 959/13, 1445/13, 2174/13, 1087/13, 1637/13, 2462/13, 1231/13, 1853/13, 2786/13, 1393/13, 2096/13, 1048/13, 524/13, 262/13 ]
Rcwa mappings can be Viewed, Displayed, Printed and written to a String. The output of the View method is kept reasonably short. In most cases it does not describe an rcwa mapping completely. In these cases the output is enclosed in brackets. There are options CycleNotation, AsClassMapping, PrintNotation and AbridgedNotation to take influence on how certain rcwa mappings are shown. These options can either be not set, set to true or set to false. If the option CycleNotation is set, it is tried harder to write down an rcwa permutation of ℤ of finite order as a product of disjoint residue class cycles, if this is possible. If the option AsClassMapping is set, Display shows which residue classes are mapped to which by the affine partial mappings, and marks any loops. The option PrintNotation influences the output in favour of GAP - readability, and the option AbridgedNotation can be used to abridge longer names like ClassShift, ClassReflection etc.. By default, the output of the methods for Display and Print describes an rcwa mapping in full. The Printed representation of an rcwa mapping is GAP - readable if and only if the Printed representation of the elements of the underlying ring is so.
There is also an operation LaTeXStringRcwaMapping, which takes as argument an rcwa mapping and returns a corresponding LaTeX string. The output makes use of the LaTeX macro package amsmath. If the option Factorization is set and the argument is bijective, a factorization into class shifts, class reflections, class transpositions and prime switches is printed (cf. FactorizationIntoCSCRCT (2.5-2)). For rcwa mappings with modulus greater than 1, an indentation by Indentation characters can be obtained by setting this option value accordingly.
gap> Print(LaTeXStringRcwaMapping(T)); n \ \mapsto \ \begin{cases} n/2 & \text{if} \ n \in 0(2), \\ (3n+1)/2 & \text{if} \ n \in 1(2). \end{cases}
There is an operation LaTeXAndXDVI which displays an rcwa mapping in an xdvi window. This works as follows: The string returned by LaTeXStringRcwaMapping is inserted into a LaTeX template file. This file is LaTeX'ed, and the result is shown with xdvi. Calling Display with option xdvi has the same effect. The operation LaTeXAndXDVI is only available on UNIX systems, and requires suitable installations of LaTeX and xdvi.
Testing rcwa mappings for equality requires only comparing their coefficient lists, hence is cheap. Rcwa mappings can be multiplied, thus there is a method for *. Rcwa permutations can also be inverted, thus there is a method for Inverse. The latter method is usually accessed by raising a mapping to a power with negative exponent. Multiplying, inverting and computing powers of tame rcwa mappings is cheap. Computing powers of wild mappings is usually expensive -- run time and memory requirements normally grow approximately exponentially with the exponent. How expensive multiplying a couple of wild mappings is, varies very much. In any case, the amount of memory required for storing an rcwa mapping is proportional to its modulus. Whether a given mapping is tame or wild can be determined by the operation IsTame. There is a method for Order, which can not only compute a finite order, but which can also detect infinite order.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> a := RcwaMapping([[2,0,3],[4,-1,3],[4,1,3]]);; # Collatz' permutation. gap> List([-4..4],k->Modulus(a^k)); [ 256, 64, 16, 4, 1, 3, 9, 27, 81 ] gap> IsTame(T) or IsTame(a); false gap> IsTame(ClassShift(0,1)) and IsTame(ClassTransposition(0,2,1,2)); true gap> T^2*a*T*a^-3; <rcwa mapping of Z with modulus 768> gap> (ClassShift(1,3)*ClassReflection(2,7))^1000000; <rcwa permutation of Z with modulus 21>
There are methods installed for IsInjective, IsSurjective, IsBijective and Image.
gap> [ IsInjective(T), IsSurjective(T), IsBijective(a) ]; [ false, true, true ] gap> Image(RcwaMapping([[2,0,1]])); 0(2)
Images of elements, of finite sets of elements and of unions of finitely many residue classes of the source of an rcwa mapping can be computed with ^, the same symbol as used for exponentiation and conjugation. The same works for partitions of the source into a finite number of residue classes.
gap> 15^T; 23 gap> ResidueClass(1,2)^T; 2(3) gap> List([[0,3],[1,3],[2,3]],ResidueClass)^a; [ 0(2), 1(4), 3(4) ]
For computing preimages of elements under rcwa mappings, there are methods for PreImageElm and PreImagesElm. The preimage of a finite set of ring elements or of a union of finitely many residue classes under an rcwa mapping can be computed by PreImage.
gap> PreImagesElm(T,8); [ 5, 16 ] gap> PreImage(T,ResidueClass(Integers,3,2)); Z \ 0(6) U 2(6) gap> M := [1];; l := [1];; gap> while Length(M) < 5000 do M := PreImage(T,M); Add(l,Length(M)); od; l; [ 1, 1, 2, 2, 4, 5, 8, 10, 14, 18, 26, 36, 50, 67, 89, 117, 157, 208, 277, 367, 488, 649, 869, 1154, 1534, 2039, 2721, 3629, 4843, 6458 ]
There is a method for the operation Support for computing the support of an rcwa mapping. A synonym for Support is MovedPoints. The natural density of the support of an rcwa mapping of ℤ can be computed efficiently with the operation DensityOfSupport. Likewise, the natural density of the set of fixed points of an rcwa mapping of ℤ can be computed efficiently with the operation DensityOfSetOfFixedPoints. There is also a method for RestrictedPerm for computing the restriction of an rcwa permutation to a union of residue classes which it fixes setwise.
gap> List([a,a^2],Support); [ Z \ [ -1, 0, 1 ], Z \ [ -3, -2, -1, 0, 1, 2, 3 ] ] gap> RestrictedPerm(ClassShift(0,2)*ClassReflection(1,2), > ResidueClass(0,2)); <rcwa mapping of Z with modulus 2> gap> last = ClassShift(0,2); true
Rcwa mappings can be added and subtracted pointwise. However, please note that the set of rcwa mappings of a ring does not form a ring under + and *.
gap> b := ClassShift(0,3) * a;; gap> [ Image((a + b)), Image((a - b)) ]; [ 2(4), [ -2, 0 ] ]
There are operations Modulus (abbreviated Mod) and Coefficients for retrieving the modulus and the coefficient list of an rcwa mapping. The meaning of the return values is as described in Section 2.2.
General documentation for most operations mentioned in this section can be found in the GAP reference manual. For rcwa mappings of rings other than ℤ, not for all operations applicable methods are available.
As in general a subring relation \(R_1<R_2\) does not give rise to a natural embedding of RCWA(\(R_1\)) into RCWA(\(R_2\)), there is no coercion between rcwa mappings or rcwa groups over different rings.
A number of basic attributes and properties of an rcwa mapping are derived immediately from the coefficients of its affine partial mappings. This holds for example for the multiplier and the divisor. These two values are stored as attributes Multiplier and Divisor, or for short Mult and Div. The prime set of an rcwa mapping is the set of prime divisors of the product of its modulus and its multiplier. It is stored as an attribute PrimeSet. The maximal shift of an rcwa mapping of ℤ is the maximum of the absolute values of its coefficients \(b_{r(m)}\) in the notation introduced in Section 2.1. It is stored as an attribute MaximalShift. An rcwa mapping is called class-wise translating if all of its affine partial mappings are translations, it is called integral if its divisor equals 1, and it is called balanced if its multiplier and its divisor have the same prime divisors. A class-wise translating mapping has the property IsClassWiseTranslating, an integral mapping has the property IsIntegral and a balanced mapping has the property IsBalanced. An rcwa mapping of the ring of integers or of one of its semilocalizations is called class-wise order-preserving if and only if all coefficients \(a_{r(m)}\) (cf. Section 2.1) in the numerators of the affine partial mappings are positive. The corresponding property is IsClassWiseOrderPreserving. An rcwa mapping of ℤ is called sign-preserving if it does not map nonnegative integers to negative integers or vice versa. The corresponding property is IsSignPreserving. All elements of the simple group CT(ℤ) generated by the set of all class transpositions are sign-preserving.
gap> u := RcwaMapping([[3,0,5],[9,1,5],[3,-1,5],[9,-2,5],[9,4,5]]);; gap> IsBijective(u);; Display(u); Rcwa permutation of Z with modulus 5 / | 3n/5 if n in 0(5) | (9n+1)/5 if n in 1(5) n |-> < (3n-1)/5 if n in 2(5) | (9n-2)/5 if n in 3(5) | (9n+4)/5 if n in 4(5) \ gap> Multiplier(u); 9 gap> Divisor(u); 5 gap> PrimeSet(u); [ 3, 5 ] gap> IsIntegral(u) or IsBalanced(u); false gap> IsClassWiseOrderPreserving(u) and IsSignPreserving(u); true
There are a couple of further attributes and operations related to the affine partial mappings of an rcwa mapping:
‣ LargestSourcesOfAffineMappings( f ) | ( attribute ) |
Returns: the coarsest partition of Source(f) on whose elements the rcwa mapping f is affine.
gap> LargestSourcesOfAffineMappings(ClassShift(3,7)); [ Z \ 3(7), 3(7) ] gap> LargestSourcesOfAffineMappings(ClassReflection(0,1)); [ Integers ] gap> u := RcwaMapping([[3,0,5],[9,1,5],[3,-1,5],[9,-2,5],[9,4,5]]);; gap> List( [ u, u^-1 ], LargestSourcesOfAffineMappings ); [ [ 0(5), 1(5), 2(5), 3(5), 4(5) ], [ 0(3), 1(3), 2(9), 5(9), 8(9) ] ] gap> kappa := ClassTransposition(2,4,3,4) * ClassTransposition(4,6,8,12) > * ClassTransposition(3,4,4,6); <rcwa permutation of Z with modulus 12> gap> LargestSourcesOfAffineMappings(kappa); [ 2(4), 1(4) U 0(12), 3(12) U 7(12), 4(12), 8(12), 11(12) ]
‣ FixedPointsOfAffinePartialMappings( f ) | ( attribute ) |
Returns: a list of the sets of fixed points of the affine partial mappings of the rcwa mapping f in the quotient field of its source.
The returned list contains entries for the restrictions of f to all residue classes modulo Mod(f). A list entry can either be an empty set, the source of f or a set of cardinality 1. The ordering of the entries corresponds to the ordering of the residues in AllResidues(Source(f),m).
gap> FixedPointsOfAffinePartialMappings(ClassShift(0,2)); [ [ ], Rationals ] gap> List([1..3],k->FixedPointsOfAffinePartialMappings(T^k)); [ [ [ 0 ], [ -1 ] ], [ [ 0 ], [ 1 ], [ 2 ], [ -1 ] ], [ [ 0 ], [ -7 ], [ 2/5 ], [ -5 ], [ 4/5 ], [ 1/5 ], [ -10 ], [ -1 ] ] ]
‣ Multpk( f, p, k ) | ( operation ) |
Returns: the union of the residue classes \(r(m)\) such that \(p^k||a_{r(m)}\) if \(k \geq 0\), and the union of the residue classes \(r(m)\) such that \(p^k||c_{r(m)}\) if \(k \leq 0\). In this context, \(m\) denotes the modulus of f, and \(a_{r(m)}\) and \(c_{r(m)}\) denote the coefficients of f as introduced in Section 2.1.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> [ Multpk(T,2,-1), Multpk(T,3,1) ]; [ Integers, 1(2) ] gap> u := RcwaMapping([[3,0,5],[9,1,5],[3,-1,5],[9,-2,5],[9,4,5]]);; gap> [ Multpk(u,3,0), Multpk(u,3,1), Multpk(u,3,2), Multpk(u,5,-1) ]; [ [ ], 0(5) U 2(5), Z \ 0(5) U 2(5), Integers ]
There are attributes ClassWiseOrderPreservingOn, ClassWiseConstantOn and ClassWiseOrderReversingOn which store the union of the residue classes (mod Mod(f)) on which an rcwa mapping f of ℤ or of a semilocalization thereof is class-wise order-preserving, class-wise constant or class-wise order-reversing, respectively.
gap> List([ClassTransposition(1,2,0,4),ClassShift(2,3), > ClassReflection(2,5)],ClassWiseOrderPreservingOn); [ Integers, Integers, Z \ 2(5) ]
Also there are attributes ShiftsUpOn and ShiftsDownOn which store the union of the residue classes (mod Mod(f)) on which an rcwa mapping f of ℤ induces affine mappings \(n \mapsto n + c\) for \(c > 0\), respectively, \(c < 0\).
Finally, there are epimorphisms from the subgroup of RCWA(ℤ) formed by all class-wise order-preserving elements to (ℤ,+) and from RCWA(ℤ) itself to the cyclic group of order 2, respectively:
‣ Determinant( f ) | ( method ) |
Returns: the determinant of the rcwa mapping f of ℤ.
The determinant of an affine mapping \(n \mapsto (an+b)/c\) whose source is a residue class \(r(m)\) is defined by \(b/|a|m\). This definition is extended additively to determinants of rcwa mappings.
Let \(f\) be an rcwa mapping of the integers, and let \(m\) denote its modulus. Using the notation \(f|_{r(m)}: n \mapsto (a_{r(m)} \cdot n + b_{r(m)})/c_{r(m)}\) for the affine partial mappings, the determinant det(\(f\)) of \(f\) is given by
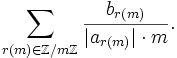
The determinant mapping is an epimorphism from the group of all class-wise order-preserving rcwa permutations of ℤ to (ℤ,+), see [Koh05], Theorem 2.11.9.
gap> List([ClassTransposition(0,4,5,12),ClassShift(3,7)],Determinant); [ 0, 1 ] gap> Determinant(ClassTransposition(0,4,5,12)*ClassShift(3,7)^100); 100
‣ Sign( g ) | ( attribute ) |
Returns: the sign of the rcwa permutation g of ℤ.
Let \(\sigma\) be an rcwa permutation of the integers, and let \(m\) denote its modulus. Using the notation \(\sigma|_{r(m)}: n \mapsto (a_{r(m)} \cdot n + b_{r(m)})/c_{r(m)}\) for the affine partial mappings, the sign of \(\sigma\) is defined by
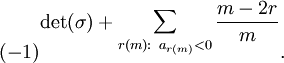
The sign mapping is an epimorphism from RCWA(ℤ) to the group \(ℤ^\times\) of units of ℤ, see [Koh05], Theorem 2.12.8. Therefore the kernel of the sign mapping is a normal subgroup of RCWA(ℤ) of index 2. The simple group CT(ℤ) is a subgroup of this kernel.
gap> List([ClassTransposition(3,4,2,6), > ClassShift(0,3),ClassReflection(2,5)],Sign); [ 1, -1, -1 ]
Factoring group elements into the members of some nice
set of generators is often helpful. In this section we describe an operation which attempts to solve this problem for the group RCWA(ℤ). Elements of finitely generated rcwa groups can be factored into generators as usual
, see PreImagesRepresentative (3.2-3).
‣ CTCSCRSplit( g ) | ( operation ) |
Returns: a list of 3 rcwa permutations \(a\), \(b\) and \(c\) whose product equals g, where \(a\) fixes the nonnegative integers setwise, \(b\) is integral and class-wise order-preserving and \(c\) is integral.
Assuming the hypothesis that CT(ℤ) is the group of all rcwa permutations of ℤ which fix the nonnegative integers setwise, \(a\) is always an element of CT(ℤ).
gap> g := ClassTransposition(0,4,1,6)*ClassShift(2,5)*ClassReflection(2,3); <rcwa permutation of Z with modulus 180> gap> facts := CTCSCRSplit(g); [ <rcwa permutation of Z with modulus 60>, ClassShift( 2(30) ), ClassReflection( 2(3) ) ] gap> Product(facts) = g; true gap> List(facts,IsSignPreserving); [ true, false, false ] gap> List(facts,IsIntegral); [ false, true, true ] gap> List(facts,IsClassWiseOrderPreserving); [ true, true, false ]
‣ FactorizationIntoCSCRCT( g ) | ( attribute ) |
‣ Factorization( g ) | ( method ) |
Returns: a factorization of the rcwa permutation g of ℤ into class shifts, class reflections and class transpositions, provided that such a factorization exists and the method finds it.
The method may return fail, stop with an error message or run into an infinite loop. If it returns a result, this result is always correct.
The problem of obtaining a factorization as described is algorithmically difficult, and this factorization routine is currently perhaps the most sophisticated part of the RCWA package. Information about the progress of the factorization process can be obtained by setting the info level of the Info class InfoRCWA (9.4-1) to 2.
By default, prime switches (\(\rightarrow\) PrimeSwitch (2.5-3)) are taken as one factor. If the option ExpandPrimeSwitches is set, they are each decomposed into the 6 class transpositions given in the definition.
By default, the factoring process begins with splitting off factors from the right. This can be changed by setting the option Direction to "from the left".
By default, a reasonably coarse respected partition of the integral mapping occurring in the final stage of the algorithm is computed. This can be suppressed by setting the option ShortenPartition equal to false.
By default, at the end it is checked whether the product of the determined factors indeed equals g. This check can be suppressed by setting the option NC.
gap> Factorization(Comm(ClassShift(0,3)*ClassReflection(1,2), > ClassShift(0,2))); [ ClassReflection( 2(3) ), ClassShift( 2(6) )^-1, ( 0(6), 2(6) ), ( 0(6), 5(6) ) ]
For purposes of demonstrating the capabilities of the factorization routine, in Section 7.2 Collatz' permutation is factored. Lothar Collatz has investigated this permutation in 1932. Its cycle structure is unknown so far.
The permutations of the following kind play an important role in factoring rcwa permutations of ℤ into class shifts, class reflections and class transpositions:
‣ PrimeSwitch( p ) | ( method ) |
‣ PrimeSwitch( p, k ) | ( method ) |
‣ PrimeSwitch( p, r, m ) | ( method ) |
‣ PrimeSwitch( p, cl ) | ( method ) |
Returns: in the first form the prime switch \(\sigma_p := \tau_{0(8),1(2p)} \cdot \tau_{4(8),-1(2p)} \cdot \tau_{0(4),1(2p)} \cdot \tau_{2(4),-1(2p)} \cdot \tau_{2(2p),1(4p)} \cdot \tau_{4(2p),2p+1(4p)}\), in the second form the restriction of \(\sigma_p\) by \(n \mapsto kn\), and in the third and fourth form the prime switch \(\sigma_{p,r(m)} := \tau_{r_1(m/2),r_2(m)} \cdot \tau_{r_2(m),r_1(pm/2)} \cdot \tau_{r(m/2),r_1(pm/2)}\). In the latter case, cl is the residue class \(r(m)\), the residue \(r_1\) is \(1-(r \mod 2)\), and \(r_2\) is defined by the equality \(r(m) \cup r_2(m) = r(m/2)\).
For an odd prime \(p\), the prime switch \(\sigma_p\) is an rcwa permutation of ℤ with modulus \(4p\), multiplier \(p\) and divisor 2. The prime switch \(\sigma_{p,r(m)}\) has multiplier \(p\) and divisor 2, and the class where the multiplication by \(p\) occurs is just \(r(m)\). The key mathematical property of a prime switch is that it is a product of class transpositions whose multiplier and divisor are coprime.
Prime switches can be distinguished from other rcwa mappings by their GAP property IsPrimeSwitch.
gap> Display(PrimeSwitch(3)); Wild rcwa permutation of Z with modulus 12 / | (3n+4)/2 if n in 2(4) | n-1 if n in 5(6) U 8(12) | n+1 if n in 1(6) n |-> < n/2 if n in 0(12) | n-3 if n in 4(12) | n if n in 3(6) | \ gap> Display(PrimeSwitch(3):AsClassMapping); Wild rcwa permutation of Z with modulus 12 0(12) -> 0(6) loop 1(6) -> 2(6) 2(4) -> 5(6) 3(6) -> 3(6) id 4(12) -> 1(12) 5(6) -> 4(6) 8(12) -> 7(12) gap> Factorization(PrimeSwitch(3)); [ ( 1(6), 0(8) ), ( 5(6), 4(8) ), ( 0(4), 1(6) ), ( 2(4), 5(6) ), ( 2(6), 1(12) ), ( 4(6), 7(12) ) ] gap> Display(PrimeSwitch(5,3,4)); Wild rcwa permutation of Z with modulus 20 / | n+1 if n in 0(2) | 5n-5 if n in 3(4) n |-> < (n-1)/2 if n in 1(4) \ 1(20) | n-1 if n in 1(20) | \ gap> Multpk(PrimeSwitch(5,3,4),5,1); 3(4) gap> PrimeSwitch(5,3,4) = PrimeSwitch(5,ResidueClass(3,4)); true gap> Factorization(PrimeSwitch(5,3,4)); [ ( 0(2), 1(4) ), ( 1(4), 0(10) ), ( 1(2), 0(10) ) ]
Obtaining a factorization of an rcwa permutation into class shifts, class reflections and class transpositions is particularly difficult if multiplier and divisor are coprime. A prototype of permutations which have this property has been introduced in a different context in [Kel99]:
‣ mKnot( m ) | ( function ) |
Returns: the permutation \(g_m\) as defined in [Kel99].
The argument m must be an odd integer greater than 1.
gap> Display(mKnot(5)); Wild rcwa permutation of Z with modulus 5 / | 6n/5 if n in 0(5) | (4n+1)/5 if n in 1(5) n |-> < (6n-2)/5 if n in 2(5) | (4n+3)/5 if n in 3(5) | (6n-4)/5 if n in 4(5) \
In his article, Timothy P. Keller shows that a permutation of this type cannot have infinitely many cycles of any given finite length.
‣ Root( f, k ) | ( method ) |
Returns: an rcwa mapping g such that g^k=f, provided that such a mapping exists and that there is a method available which can determine it.
Currently, extracting roots is implemented for rcwa permutations of finite order.
gap> Root(ClassTransposition(0,2,1,2),100); ( 0(8), 2(8), 4(8), 6(8), 1(8), 3(8), 5(8), 7(8) ) gap> Display(last:CycleNotation:=false); Tame rcwa permutation of Z with modulus 8 / | n+2 if n in Z \ 6(8) U 7(8) n |-> < n-5 if n in 6(8) | n-7 if n in 7(8) \ gap> last^100 = ClassTransposition(0,2,1,2); true
‣ RightInverse( f ) | ( attribute ) |
Returns: a right inverse of the injective rcwa mapping f, i.e. a mapping \(g\) such that f\(g\) = 1.
gap> twice := 2*IdentityRcwaMappingOfZ; Rcwa mapping of Z: n -> 2n gap> twice * RightInverse(twice); IdentityMapping( Integers )
‣ CommonRightInverse( l, r ) | ( operation ) |
Returns: a mapping \(d\) such that l\(d\) = r\(d\) = 1.
The mappings l and r must be injective, and their images must form a partition of their source.
gap> twice := 2*IdentityRcwaMappingOfZ; twiceplus1 := twice+1; Rcwa mapping of Z: n -> 2n Rcwa mapping of Z: n -> 2n + 1 gap> Display(CommonRightInverse(twice,twiceplus1)); Rcwa mapping of Z with modulus 2 / | n/2 if n in 0(2) n |-> < (n-1)/2 if n in 1(2) | \
‣ ImageDensity( f ) | ( attribute ) |
Returns: the image density of the rcwa mapping f.
In the notation introduced in the definition of an rcwa mapping, the image density of an rcwa mapping \(f\) is defined by 1/m \(\sum_{r(m) \in R/mR} |R/c_{r(m)}R|/|R/a_{r(m)}R|\). The image density of an injective rcwa mapping is \(\leq 1\), and the image density of a surjective rcwa mapping is \(\geq 1\) (this can be seen easily). Thus in particular the image density of a bijective rcwa mapping is 1.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> List( [ T, ClassShift(0,1), RcwaMapping([[2,0,1]]) ], ImageDensity ); [ 4/3, 1, 1/2 ]
Given an rcwa mapping f, the function InjectiveAsMappingFrom returns a set S such that the restriction of f to S is injective, and such that the image of S under f is the entire image of f.
gap> InjectiveAsMappingFrom(T); 0(2)
RCWA provides various methods to compute trajectories of rcwa mappings:
‣ Trajectory( f, n, length ) | ( method ) |
‣ Trajectory( f, n, length, m ) | ( method ) |
‣ Trajectory( f, n, terminal ) | ( method ) |
‣ Trajectory( f, n, terminal, m ) | ( method ) |
Returns: the first length iterates in the trajectory of the rcwa mapping f starting at n, respectively the initial part of the trajectory of the rcwa mapping f starting at n which ends at the first occurrence of an iterate in the set terminal. If the argument m is given, the iterates are reduced (mod m).
To save memory when computing long trajectories containing huge iterates, the reduction (mod m) is done each time before storing an iterate. In place of the ring element n, the methods also accept a finite set of ring elements or a union of residue classes.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> Trajectory(T,27,15); Trajectory(T,27,20,5); [ 27, 41, 62, 31, 47, 71, 107, 161, 242, 121, 182, 91, 137, 206, 103 ] [ 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 3, 0, 3, 0, 0, 3 ] gap> Trajectory(T,15,[1]); Trajectory(T,15,[1],2); [ 15, 23, 35, 53, 80, 40, 20, 10, 5, 8, 4, 2, 1 ] [ 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1 ] gap> Trajectory(T,ResidueClass(Integers,3,0),Integers); [ 0(3), 0(3) U 5(9), 0(3) U 5(9) U 7(9) U 8(27), <union of 20 residue classes (mod 27) (6 classes)>, <union of 73 residue classes (mod 81)>, Z \ 10(81) U 37(81), Integers ]
accumulated coefficients)
‣ Trajectory( f, n, length, whichcoeffs ) | ( method ) |
‣ Trajectory( f, n, terminal, whichcoeffs ) | ( method ) |
Returns: either the list c of triples of coprime coefficients such that for any k it holds that n^(f^(k-1)) = (c[k][1]*n + c[k][2])/c[k][3] or the last entry of that list, depending on whether whichcoeffs is "AllCoeffs" or "LastCoeffs".
The meanings of the arguments length and terminal are the same as in the methods for the operation Trajectory described above. In general, computing only the last coefficient triple (whichcoeffs = "LastCoeffs") needs considerably less memory than computing the entire list.
gap> Trajectory(T,27,[1],"LastCoeffs"); [ 36472996377170786403, 195820718533800070543, 1180591620717411303424 ] gap> (last[1]*27+last[2])/last[3]; 1
When dealing with problems like the \(3n+1\)-Conjecture or when determining the degree of transitivity of the natural action of an rcwa group on its underlying ring, an important task is to determine the residue classes whose elements get larger or smaller when applying a given rcwa mapping:
‣ IncreasingOn( f ) | ( attribute ) |
‣ DecreasingOn( f ) | ( attribute ) |
Returns: the union of all residue classes \(r(m)\) such that \(|R/a_{r(m)}R| > |R/c_{r(m)}R|\) or \(|R/a_{r(m)}R| < |R/c_{r(m)}R|\), respectively, where \(R\) denotes the source, \(m\) denotes the modulus and \(a_{r(m)}\), \(b_{r(m)}\) and \(c_{r(m)}\) denote the coefficients of f as introduced in Section 2.1.
If the argument is an rcwa mapping of ℤ in sparse representation, an option classes is interpreted; if set, the step of forming the union of the residue classes in question is omitted, and the list of residue classes is returned instead of their union. This may save time and memory if the modulus is large.
gap> List([1..3],k->IncreasingOn(T^k)); [ 1(2), 3(4), 3(4) U 1(8) U 6(8) ] gap> List([1..3],k->DecreasingOn(T^k)); [ 0(2), Z \ 3(4), 0(4) U 2(8) U 5(8) ] gap> a := RcwaMapping([[2,0,3],[4,-1,3],[4,1,3]]);; # Collatz' permutation gap> List([-2..2],k->IncreasingOn(a^k)); [ Z \ 1(8) U 7(8), 0(2), [ ], Z \ 0(3), 1(9) U 4(9) U 5(9) U 8(9) ]
We assign certain directed graphs to rcwa mappings, which encode the order in which trajectories may traverse the residue classes modulo some modulus:
‣ TransitionGraph( f, m ) | ( operation ) |
Returns: the transition graph of the rcwa mapping f for modulus m.
The transition graph \(\Gamma_{f,m}\) of \(f\) for modulus \(m\) is defined as follows:
The vertices are the residue classes (mod \(m\)).
There is an edge from \(r_1(m)\) to \(r_2(m)\) if and only if there is some \(n \in r_1(m)\) such that \(n^f \in r_2(m)\).
The assignment of the residue classes (mod \(m\)) to the vertices of the graph corresponds to the ordering of the residues in AllResidues(Source(f),m). The result is returned in the format used by the package GRAPE [Soi16].
There are a couple of operations and attributes which are based on these graphs:
‣ OrbitsModulo( f, m ) | ( operation ) |
Returns: the partition of AllResidues(Source(f),m) corresponding to the weakly connected components of the transition graph of the rcwa mapping f for modulus m.
gap> OrbitsModulo(ClassTransposition(0,2,1,4),8); [ [ 0, 1, 4 ], [ 2, 5, 6 ], [ 3 ], [ 7 ] ]
‣ FactorizationOnConnectedComponents( f, m ) | ( operation ) |
Returns: the set of restrictions of the rcwa mapping f to the weakly connected components of its transition graph \(\Gamma_{f,m}\).
The product of the returned mappings is f. They have pairwise disjoint supports, hence any two of them commute.
gap> sigma := ClassTransposition(1,4,2,4) * ClassTransposition(1,4,3,4) > * ClassTransposition(3,9,6,18) * ClassTransposition(1,6,3,9);; gap> List(FactorizationOnConnectedComponents(sigma,36),Support); [ 33(36) U 34(36) U 35(36), 9(36) U 10(36) U 11(36), <union of 23 residue classes (mod 36)> \ [ -6, 3 ] ]
‣ TransitionMatrix( f, m ) | ( operation ) |
Returns: the transition matrix of the rcwa mapping f for modulus m.
Let \(M\) be this matrix. Then for any two residue classes \(r_1(m), r_2(m) \in R/mR\), the entry \(M_{r_1(m),r_2(m)}\) is defined by
AllResidues(Source(f),m).
The transition matrix is a weighted adjacency matrix of the corresponding transition graph TransitionGraph(f,m). The sums of the rows of a transition matrix are always equal to 1.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> Display(TransitionMatrix(T^3,3)); [ [ 1/8, 1/4, 5/8 ], [ 0, 1/4, 3/4 ], [ 0, 3/8, 5/8 ] ]
‣ Sources( f ) | ( attribute ) |
‣ Sinks( f ) | ( attribute ) |
Returns: a list of unions of residue classes modulo the modulus \(m\) of the rcwa mapping f, as described below.
The returned list contains an entry for any strongly connected component of the transition graph of f for modulus Mod(f) which has only outgoing edges (source
) or which has only ingoing edges (sink
), respectively. The list entry corresponding to such a component is the union of the vertices belonging to it.
gap> g := ClassTransposition(0,2,1,2)*ClassTransposition(0,2,1,4);; gap> Sources(g); Sinks(g); [ 0(4) ] [ 1(4) ]
‣ Loops( f ) | ( attribute ) |
Returns: if f is bijective, the list of non-isolated vertices of the transition graph of f for modulus Mod(f) which carry a loop. In general, the list of vertices of that transition graph which carry a loop, but which f does not fix setwise.
The returned list may also include supersets of the named residue classes instead if f is affine even on these.
gap> Loops(ClassTransposition(0,2,1,2)*ClassTransposition(0,2,1,4)); [ 0(4), 1(4) ]
There is a nice invariant of trajectories of the Collatz mapping:
‣ GluckTaylorInvariant( a ) | ( function ) |
Returns: the invariant defined in [GT02]. This is \((\sum_{i=1}^l a_i \cdot a_{i \mod l + 1})/(\sum_{i=1}^l a_i^2)\), where \(l\) denotes the length of a.
The argument a must be a list of integers. In [GT02] it is shown that if a is a trajectory of the `original' Collatz mapping \(n\) \(\mapsto\) (\(n/2\) if \(n\) even, \(3n+1\) if \(n\) odd) starting at an odd integer \(\geq 3\) and ending at 1, then the invariant lies in the interval \(]9/13,5/7[\).
gap> C := RcwaMapping([[1,0,2],[3,1,1]]);; gap> List([3,5..49],n->Float(GluckTaylorInvariant(Trajectory(C,n,[1])))); [ 0.701053, 0.696721, 0.708528, 0.707684, 0.706635, 0.695636, 0.711769, 0.699714, 0.707409, 0.693833, 0.710432, 0.706294, 0.714242, 0.699935, 0.714242, 0.705383, 0.706591, 0.698198, 0.712222, 0.714242, 0.709048, 0.69612, 0.714241, 0.701076 ]
Quite often one can make certain educated guesses
on the overall behaviour of the trajectories of a given rcwa mapping. For example it is reasonably straightforward to make the conjecture that all trajectories of the Collatz mapping eventually enter the finite set \(\{-136, -91, -82, -68, -61, -55, -41, -37, -34, -25, -17, -10, -7, -5, -1, 0, 1, 2 \}\), or that on average
the next number in a trajectory of the Collatz mapping is smaller than the preceding one by a factor of \(\sqrt{3}/2\). However it is clear that such guesses can be wrong, and that they therefore cannot be used to prove anything. Nevertheless they can sometimes be useful:
‣ LikelyContractionCentre( f, maxn, bound ) | ( operation ) |
Returns: a list of ring elements (see below).
This operation tries to compute the contraction centre of the rcwa mapping f. Assuming its existence this is the unique finite subset \(S_0\) of the source of f on which f induces a permutation and which intersects non-trivially with any trajectory of f. The mapping f is assumed to be contracting, i.e. to have such a contraction centre. As in general contraction centres are likely not computable, the methods for this operation are probabilistic and may return wrong results. The argument maxn is a bound on the starting value and bound is a bound on the elements of the trajectories to be searched. If the limit bound is exceeded, an Info message on Info level 3 of InfoRCWA is given.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; # The Collatz mapping. gap> S0 := LikelyContractionCentre(T,100,1000); #I Warning: `LikelyContractionCentre' is highly probabilistic. The returned result can only be regarded as a rough guess. See ?LikelyContractionCentre for more information. [ -136, -91, -82, -68, -61, -55, -41, -37, -34, -25, -17, -10, -7, -5, -1, 0, 1, 2 ]
‣ GuessedDivergence( f ) | ( operation ) |
Returns: a floating point value which is intended to be a rough guess on how fast the trajectories of the rcwa mapping f diverge (return value greater than 1) or converge (return value smaller than 1).
Nothing particular is guaranteed.
gap> GuessedDivergence(T); #I Warning: GuessedDivergence: no particular return value is guaranteed. 0.866025
It is quite common that an rcwa mapping with large modulus has only few distinct affine partial mappings. In this case the standard
representation which stores a coefficient triple for each residue class modulo the modulus is unsuitable. For this reason there is a second representation of rcwa mappings, the sparse
representation. Depending on the rcwa mappings involved, using this representation may speed up computations and reduce memory requirements by orders of magnitude. For rcwa mappings with almost as many distinct affine partial mappings as there are residue classes modulo the modulus, using sparse representation makes computations slower and more memory-consuming. Presently, the sparse representation is only available for rcwa mappings of ℤ.
The sparse representation of an rcwa mapping consists of the modulus and a list of 5-tuples \((r,m,a_{r(m)},b_{r(m)},c_{r(m)})\) of integers. Any such 5-tuple specifies the coefficients of the restriction \(n \mapsto (a_{r(m)} \cdot n + b_{r(m)})/c_{r(m)}\) of the mapping to a residue class \(r(m)\). The \(r(m)\) are chosen to form the coarsest possible partition of ℤ into residue classes such that the restriction of the mapping to any of them is affine. Also the list of coefficient tuples is sorted, all \(c_{r(m)}\) are positive and \(\gcd(c_{r(m)},\gcd(a_{r(m)},b_{r(m)})) = 1\). This way the coefficient list of an rcwa mapping of ℤ is unique.
Changing the representation of rcwa mappings does not change their behaviour with respect to
and =
The product of two rcwa mappings in sparse representation is in sparse representation again, just like the product of two rcwa mappings in standard representation is in standard representation. Also, inverses are in the same representation. The product of two rcwa mappings in different representation may be in any of the representations of the factors.<
‣ SparseRepresentation( f ) | ( operation ) |
‣ SparseRep( f ) | ( operation ) |
‣ StandardRepresentation( f ) | ( operation ) |
‣ StandardRep( f ) | ( operation ) |
Returns: the rcwa mapping f in sparse, respectively, standard representation.
Appropriate attribute values and properties are copied over to the rcwa mapping in the new
representation.
gap> a := ClassTransposition(1,2,4,6); ( 1(2), 4(6) ) gap> b := ClassTransposition(1,3,2,6); ( 1(3), 2(6) ) gap> c := ClassTransposition(2,3,4,6); ( 2(3), 4(6) ) gap> g := (b*a*c)^2*a; <rcwa permutation of Z with modulus 288> gap> h := SparseRep(g); <rcwa permutation of Z with modulus 288 and 21 affine parts> gap> g = h; true gap> Coefficients(h); [ [ 0, 6, 1, 0, 1 ], [ 1, 3, 16, -1, 3 ], [ 2, 96, 9, 14, 16 ], [ 3, 24, 9, 5, 4 ], [ 5, 24, 3, 1, 4 ], [ 8, 36, 2, -7, 9 ], [ 9, 48, 27, 29, 8 ], [ 11, 24, 9, 5, 4 ], [ 14, 48, 27, 38, 8 ], [ 15, 24, 27, 19, 4 ], [ 17, 48, 9, 7, 8 ], [ 20, 72, 3, 4, 4 ], [ 21, 24, 1, -3, 6 ], [ 23, 24, 27, 19, 4 ], [ 26, 48, 3, 2, 8 ], [ 32, 36, 4, -11, 9 ], [ 33, 48, 9, 7, 8 ], [ 38, 48, 9, 10, 8 ], [ 41, 48, 27, 29, 8 ], [ 50, 96, 27, 58, 16 ], [ 56, 72, 1, 0, 4 ] ] gap> h^2; <rcwa permutation of Z with modulus 13824 and 71 affine parts> gap> h^3; <rcwa permutation of Z with modulus 663552 and 201 affine parts>
Memory consumption may differ a lot between sparse- and standard representation:
gap> MemoryUsage(h^3); # on a 64-bit machine 18254 gap> MemoryUsage(StandardRep(h^3)); # on a 64-bit machine 42467894
‣ IsRcwaMapping( f ) | ( filter ) |
‣ IsRcwaMappingOfZ( f ) | ( filter ) |
‣ IsRcwaMappingOfZ_pi( f ) | ( filter ) |
‣ IsRcwaMappingOfGFqx( f ) | ( filter ) |
Returns: true if f is an rcwa mapping, an rcwa mapping of the ring of integers, an rcwa mapping of a semilocalization of the ring of integers or an rcwa mapping of a polynomial ring in one variable over a finite field, respectively, and false otherwise.
Often the same methods can be used for rcwa mappings of the ring of integers and of its semilocalizations. For this reason there is a category IsRcwaMappingOfZOrZ_pi which is the union of IsRcwaMappingOfZ and IsRcwaMappingOfZ_pi. The internal representation of rcwa mappings is called IsRcwaMappingStandardRep. There are methods available for ExtRepOfObj and ObjByExtRep.
‣ RcwaMappingsFamily( R ) | ( function ) |
Returns: the family of rcwa mappings of the ring R.
generated by GAPDoc2HTML