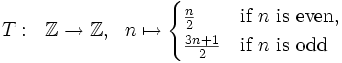
This chapter discusses a number of examples of rcwa mappings and -groups in detail. All of them show different aspects of the package, and the order in which they appear is entirely arbitrary. In particular they are not ordered by degree of difficulty or interest.
The rcwa mappings, rcwa groups and other objects defined in this chapter can be found in the file pkg/rcwa/examples/examples.g. This file can be read into the current GAP session by the function LoadRCWAExamples (6.1-1) which takes no arguments and returns the name of a variable which the record containing the examples got assigned to. The global variable assignments made in a section of this chapter can be made by applying the function AssignGlobals to the respective component of the examples record. The component names are given at the end of the corresponding sections.
The discussions of the examples are typically far from being exhaustive. It is quite likely that in many instances by just a few little modifications or additional easy commands you can find out interesting things yourself -- have fun!
Thompson's group V, also known as Higman-Thompson group, is a finitely presented infinite simple group. This group has been found by Graham Higman, cf. [Hig74]. We show that the group
gap> G := Group(List([[0,2,1,4],[0,4,1,4],[1,4,2,4],[2,4,3,4]], > ClassTransposition)); <(0(2),1(4)),(0(4),1(4)),(1(4),2(4)),(2(4),3(4))>
is isomorphic to Thompson's group V. This isomorphism has been pointed out by John P. McDermott. We take a slightly different set of generators:
gap> k := ClassTransposition(0,2,1,2);; gap> l := ClassTransposition(1,2,2,4);; gap> m := ClassTransposition(0,2,1,4);; gap> n := ClassTransposition(1,4,2,4);; gap> H := Group(k,l,m,n); <(0(2),1(2)),(1(2),2(4)),(0(2),1(4)),(1(4),2(4))> gap> G = H; # k, l, m and n generate G as well true
Now we verify that our four generators satisfy the relations given on page 50 in [Hig74], when we read k as \(\kappa\), l as \(\lambda\), m as \(\mu\) and n as \(\nu\):
gap> HigmanThompsonRels := > [ k^2, l^2, m^2, n^2, # (1) in Higman's book > l*k*m*k*l*n*k*n*m*k*l*k*m, # (2) " > k*n*l*k*m*n*k*l*n*m*n*l*n*m, # (3) " > (l*k*m*k*l*n)^3, (m*k*l*k*m*n)^3, # (4) " > (l*n*m)^2*k*(m*n*l)^2*k, # (5) " > (l*n*m*n)^5, # (6) " > (l*k*n*k*l*n)^3*k*n*k*(m*k*n*k*m*n)^3*k*n*k*n,# (7) " > ((l*k*m*n)^2*(m*k*l*n)^2)^3, # (8) " > (l*n*l*k*m*k*m*n*l*n*m*k*m*k)^4, # (9) " > (m*n*m*k*l*k*l*n*m*n*l*k*l*k)^4, #(10) " > (l*m*k*l*k*m*l*k*n*k)^2, #(11) " > (m*l*k*m*k*l*m*k*n*k)^2 ]; #(12) " [ IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ), IdentityMapping( Integers ) ]
We conclude that our group is an homomorphic image of Thompson's group V. But since Thompson's group V is simple and our group is not trivial, this means indeed that the two groups are isomorphic.
In fact it is straightforward to show that G is the group CT([2],Integers) which is generated by the set of all class transpositions which interchange residue classes modulo powers of 2. First we check that G contains all 11 class transpositions which interchange residue classes modulo 2 or 4:
gap> S := Filtered(List(ClassPairs(4),ClassTransposition), > ct->Mod(ct) in [2,4]); [ ( 0(2), 1(2) ), ( 0(2), 1(4) ), ( 0(2), 3(4) ), ( 0(4), 1(4) ), ( 0(4), 2(4) ), ( 0(4), 3(4) ), ( 1(2), 0(4) ), ( 1(2), 2(4) ), ( 1(4), 2(4) ), ( 1(4), 3(4) ), ( 2(4), 3(4) ) ] gap> IsSubset(G,S); true
Then we give a function which takes a class transposition \(\tau \in {\rm CT}_\emptyset(ℤ)\), and which returns a factorization of an element \(\gamma\) satisfying \(\tau^\gamma \in S\) into \(g_1 := \tau_{0(2),1(4)} \in S\), \(g_2 := \tau_{0(2),3(4)} \in S\), \(g_3 := \tau_{1(2),0(4)} \in S\), \(g_4 := \tau_{1(2),2(4)} \in S\), \(h_1 := \tau_{0(4),1(4)} \in S\) and \(h_2 := \tau_{1(4),2(4)} \in S\):
ReducingConjugator := function ( tau )
local w, F, g1, g2, g3, g4, h1, h2, h, cls, cl, r;
g1 := ClassTransposition(0,2,1,4); h1 := ClassTransposition(0,4,1,4);
g2 := ClassTransposition(0,2,3,4); h2 := ClassTransposition(1,4,2,4);
g3 := ClassTransposition(1,2,0,4);
g4 := ClassTransposition(1,2,2,4);
F := FreeGroup("g1","g2","g3","g4","h1","h2");
w := One(F); if Mod(tau) <= 4 then return w; fi;
# Before we can reduce the moduli of the interchanged residue classes,
# we must make sure that both of them have at least modulus 4.
cls := TransposedClasses(tau);
if Mod(cls[1]) = 2 then
if Residue(cls[1]) = 0 then
if Residue(cls[2]) mod 4 = 1 then tau := tau^g2; w := w * F.2;
else tau := tau^g1; w := w * F.1; fi;
else
if Residue(cls[2]) mod 4 = 0 then tau := tau^g4; w := w * F.4;
else tau := tau^g3; w := w * F.3; fi;
fi;
fi;
while Mod(tau) > 4 do # Now we can successively reduce the moduli.
if not ForAny(AllResidueClassesModulo(2),
cl -> IsEmpty(Intersection(cl,Support(tau))))
then
cls := TransposedClasses(tau);
h := Filtered([h1,h2],
hi->Length(Filtered(cls,cl->IsSubset(Support(hi),cl)))=1);
h := h[1]; tau := tau^h;
if h = h1 then w := w * F.5; else w := w * F.6; fi;
fi;
cl := TransposedClasses(tau)[2]; # class with larger modulus
r := Residue(cl);
if r mod 4 = 1 then tau := tau^g1; w := w * F.1;
elif r mod 4 = 3 then tau := tau^g2; w := w * F.2;
elif r mod 4 = 0 then tau := tau^g3; w := w * F.3;
elif r mod 4 = 2 then tau := tau^g4; w := w * F.4; fi;
od;
return w;
end;
After assigning g1, g2, g3, g4, h1 and h2 appropriately, we obtain for example:
gap> ReducingConjugator(ClassTransposition(3,16,34,256)); h2*g1*h1*g1*h1*g1*h1*g1*h2*g2*h2*g4*h2*g4*h2*g3 gap> gamma := h2*g1*h1*g1*h1*g1*h1*g1*h2*g2*h2*g4*h2*g4*h2*g3; <rcwa permutation of Z with modulus 256> gap> ct := ClassTransposition(3,16,34,256)^gamma;; gap> IsClassTransposition(ct);; gap> ct; ClassTransposition(1,4,2,4)
Thompson's group V can also be embedded in a natural way into CT(GF(2)[x]):
gap> x := Indeterminate(GF(2));; SetName(x,"x"); gap> R := PolynomialRing(GF(2),1);; gap> k := ClassTransposition(0,x,1,x);; gap> l := ClassTransposition(1,x,x,x^2);; gap> m := ClassTransposition(0,x,1,x^2);; gap> n := ClassTransposition(1,x^2,x,x^2);; gap> G := Group(k,l,m,n); <rcwa group over GF(2)[x] with 4 generators>
The correctness of this representation can likewise be verified by simply checking the defining relations given above.
Enter AssignGlobals(LoadRCWAExamples().HigmanThompson); in order to assign the global variables defined in this section.
In 1932, Lothar Collatz mentioned in his notebook the following permutation of the integers:
gap> Collatz := RcwaMapping([[2,0,3],[4,-1,3],[4,1,3]]);; gap> Display(Collatz); Rcwa mapping of Z with modulus 3 / | 2n/3 if n in 0(3) n |-> < (4n-1)/3 if n in 1(3) | (4n+1)/3 if n in 2(3) \ gap> ShortCycles(Collatz,[-50..50],50); # There are some finite cycles: [ [ 0 ], [ -1 ], [ 1 ], [ 2, 3 ], [ -2, -3 ], [ 4, 5, 7, 9, 6 ], [ -4, -5, -7, -9, -6 ], [ 44, 59, 79, 105, 70, 93, 62, 83, 111, 74, 99, 66 ], [ -44, -59, -79, -105, -70, -93, -62, -83, -111, -74, -99, -66 ] ]
The cycle structure of Collatz' permutation has not been completely determined yet. In particular it is not known whether the cycle containing 8 is finite or infinite. Nevertheless, the factorization routine included in this package can determine a factorization of this permutation into class transpositions, i.e. involutions interchanging two disjoint residue classes:
gap> Collatz in CT(Integers); # `Collatz' lies in the simple group CT(Z). true gap> Length(Factorization(Collatz)); 212
Setting the Info level of InfoRCWA equal to 2 (simply issue RCWAInfo(2);) causes the factorization routine to display detailed information on the progress of the factoring process. For reasons of saving space, this is not done in this manual.
We would like to get a factorization into fewer factors. Firstly, we try to factor the inverse -- just like the various options interpreted by the factorization routine, this has influence on decisions taken during the factoring process:
gap> Length(Factorization(Collatz^-1)); 129
This is already a shorter product, but can still be improved. We remember the mKnot's, of which the permutation mKnot(3) looks very similar to Collatz' permutation. Therefore it is straightforward to try to factor both mKnot(3) and Collatz/mKnot(3), and to look whether the sum of the numbers of factors is less than 129:
gap> KnotFacts := Factorization(mKnot(3));; gap> QuotFacts := Factorization(Collatz/mKnot(3));; gap> List([KnotFacts,QuotFacts],Length); [ 59, 9 ] gap> CollatzFacts := Concatenation(QuotFacts,KnotFacts); [ ( 0(6), 4(6) ), ( 0(6), 5(6) ), ( 0(6), 3(6) ), ( 0(6), 1(6) ), ( 0(6), 2(6) ), ( 2(3), 4(6) ), ( 0(3), 4(6) ), ( 2(3), 1(6) ), ( 0(3), 1(6) ), ( 0(36), 35(36) ), ( 0(36), 22(36) ), ( 0(36), 18(36) ), ( 0(36), 17(36) ), ( 0(36), 14(36) ), ( 0(36), 20(36) ), ( 0(36), 4(36) ), ( 2(36), 8(36) ), ( 2(36), 16(36) ), ( 2(36), 13(36) ), ( 2(36), 9(36) ), ( 2(36), 7(36) ), ( 2(36), 6(36) ), ( 2(36), 3(36) ), ( 2(36), 10(36) ), ( 2(36), 15(36) ), ( 2(36), 12(36) ), ( 2(36), 5(36) ), ( 21(36), 28(36) ), ( 21(36), 33(36) ), ( 21(36), 30(36) ), ( 21(36), 23(36) ), ( 21(36), 34(36) ), ( 21(36), 31(36) ), ( 21(36), 27(36) ), ( 21(36), 25(36) ), ( 21(36), 24(36) ), ( 26(36), 32(36) ), ( 26(36), 29(36) ), ( 10(18), 35(36) ), ( 5(18), 35(36) ), ( 10(18), 17(36) ), ( 5(18), 17(36) ), ( 8(12), 14(24) ), ( 6(9), 17(18) ), ( 3(9), 17(18) ), ( 0(9), 17(18) ), ( 6(9), 16(18) ), ( 3(9), 16(18) ), ( 0(9), 16(18) ), ( 6(9), 11(18) ), ( 3(9), 11(18) ), ( 0(9), 11(18) ), ( 6(9), 4(18) ), ( 3(9), 4(18) ), ( 0(9), 4(18) ), ( 0(6), 14(24) ), ( 0(6), 2(24) ), ( 8(12), 17(18) ), ( 7(12), 17(18) ), ( 8(12), 11(18) ), ( 7(12), 11(18) ), PrimeSwitch(3)^-1, ( 7(12), 17(18) ), ( 2(6), 17(18) ), ( 0(3), 17(18) ), PrimeSwitch(3)^-1, PrimeSwitch(3)^-1, PrimeSwitch(3)^-1 ] gap> Product(CollatzFacts) = Collatz; # Check. true
The factors PrimeSwitch(3) are products of 6 class transpositions (cf. PrimeSwitch (2.5-3)).
Enter AssignGlobals(LoadRCWAExamples().CollatzlikePerms); in order to assign the global variables defined in this section.
The following group acts transitively on the set of positive integers for which the \(3n+1\) conjecture holds and which are not divisible by 6:
gap> a := ClassTransposition(1,2,4,6);; gap> b := ClassTransposition(1,3,2,6);; gap> c := ClassTransposition(2,3,4,6);; gap> G := Group(a,b,c); <(1(2),4(6)),(1(3),2(6)),(2(3),4(6))> gap> LoadDatabaseOfGroupsGeneratedBy3ClassTranspositions(); "3CTsGroups6" gap> 3CTsGroups6.Id3CTsGroup(G,3CTsGroups6.grps); # 'catalogue number' of G 44132
To see this, consider the action of \(G\) on the \(3n+1\) tree
. The vertices of this tree are the positive integers for which the \(3n+1\) conjecture holds, and for every vertex \(n\) there is an edge from \(n\) to \(T(n)\), where \(T\) denotes the Collatz mapping
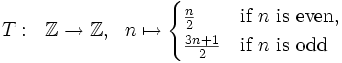
(cf. Chapter 1). It is easy to check that for every vertex \(n\), either \(a\), \(b\) or \(c\) maps \(n\) to \(T(n)\), and that the other two generators either fix \(n\) or map it to one of its preimages under \(T\). So the \(3n+1\) conjecture is equivalent to the assertion that the group \(G\) acts transitively on \(\mathbb{N} \setminus 0(6)\). First let's have a look at balls of small radius about 1 under the action of \(G\) -- these consist of those numbers whose trajectory under \(T\) reaches 1 quickly:
gap> Ball(G,1,5,OnPoints); [ 1, 2, 4, 5, 8, 10, 16, 32, 64 ] gap> Ball(G,1,10,OnPoints); [ 1, 2, 3, 4, 5, 8, 10, 13, 16, 20, 21, 26, 32, 40, 52, 53, 64, 80, 85, 128, 160, 170, 256, 320, 340, 341, 512, 1024, 2048 ] gap> Ball(G,1,15,OnPoints); [ 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 16, 17, 20, 21, 22, 23, 26, 32, 34, 35, 40, 44, 45, 46, 52, 53, 64, 68, 69, 70, 75, 80, 85, 104, 106, 113, 128, 136, 140, 141, 151, 160, 170, 208, 212, 213, 226, 227, 256, 272, 277, 280, 301, 302, 320, 340, 341, 416, 424, 452, 453, 454, 512, 640, 680, 682, 832, 848, 853, 904, 908, 909, 1024, 1280, 1360, 1364, 1365, 1664, 1696, 1706, 1808, 1813, 1816, 2048, 2560, 2720, 2728, 4096, 5120, 5440, 5456, 5461, 8192, 10240, 10880, 10912, 10922, 16384, 32768, 65536 ] gap> Ball(G,1,15,OnPoints:Spheres); [ [ 1 ], [ 2, 4 ], [ 8 ], [ 16 ], [ 5, 32 ], [ 10, 64 ], [ 3, 20, 21, 128 ], [ 40, 256 ], [ 13, 80, 85, 512 ], [ 26, 160, 170, 1024 ], [ 52, 53, 320, 340, 341, 2048 ], [ 17, 104, 106, 113, 640, 680, 682, 4096 ], [ 34, 35, 208, 212, 213, 226, 227, 1280, 1360, 1364, 1365, 8192 ], [ 11, 68, 69, 70, 75, 416, 424, 452, 453, 454, 2560, 2720, 2728, 16384 ], [ 22, 23, 136, 140, 141, 151, 832, 848, 853, 904, 908, 909, 5120, 5440, 5456, 5461, 32768 ], [ 7, 44, 45, 46, 272, 277, 280, 301, 302, 1664, 1696, 1706, 1808, 1813, 1816, 10240, 10880, 10912, 10922, 65536 ] ] gap> List(Ball(G,1,50,OnPoints:Spheres),Length); [ 1, 2, 1, 1, 2, 2, 4, 2, 4, 4, 6, 8, 12, 14, 17, 20, 26, 32, 43, 52, 66, 81, 104, 133, 170, 211, 271, 335, 424, 542, 686, 873, 1096, 1376, 1730, 2205, 2794, 3522, 4429, 5611, 7100, 8978, 11343, 14296, 18058, 22828, 28924, 36532, 46146, 58399, 73713 ] gap> FloatQuotientsList(last); [ 2., 0.5, 1., 2., 1., 2., 0.5, 2., 1., 1.5, 1.33333, 1.5, 1.16667, 1.21429, 1.17647, 1.3, 1.23077, 1.34375, 1.2093, 1.26923, 1.22727, 1.28395, 1.27885, 1.2782, 1.24118, 1.28436, 1.23616, 1.26567, 1.2783, 1.26568, 1.27259, 1.25544, 1.25547, 1.25727, 1.27457, 1.26712, 1.26056, 1.25752, 1.26688, 1.26537, 1.26451, 1.26342, 1.26034, 1.26315, 1.26415, 1.26704, 1.26303, 1.26317, 1.26553, 1.26223 ] gap> Difference(Filtered([1..100],n->n mod 6 <> 0),Ball(G,1,40,OnPoints)); [ 27, 31, 41, 47, 55, 62, 63, 71, 73, 82, 83, 91, 94, 95, 97 ] gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; gap> List(last2,n->Length(Trajectory(T,n,[1]))); [ 71, 68, 70, 67, 72, 69, 69, 66, 74, 71, 71, 60, 68, 68, 76 ]
It is convenient to define an epimorphism from the free group of rank 3 to \(G\):
gap> F := FreeGroup("a","b","c"); <free group on the generators [ a, b, c ]> gap> phi := EpimorphismByGenerators(F,G); [ a, b, c ] -> [ ( 1(2), 4(6) ), ( 1(3), 2(6) ), ( 2(3), 4(6) ) ]
We can compute balls about 1 in \(G\):
gap> B := Ball(G,One(G),7:Spheres);; gap> List(B,Length); [ 1, 3, 6, 12, 24, 48, 96, 192 ] gap> List(B[3],Order); [ 12, infinity, infinity, infinity, infinity, 12 ] gap> List(B[3],g->PreImagesRepresentative(phi,g)); [ b*a, c*b, c*a, b*c, a*c, a*b ] gap> g := a*b;; Order(g);; gap> Display(g); Rcwa permutation of Z with modulus 18, of order 12 ( 1(6), 8(36), 4(18), 2(12) ) ( 3(6), 20(36), 10(18) ) ( 5(6), 32(36), 16(18) )
Spending some more time to compute B := Ball(G,One(G),12:Spheres);;, one can check that \((ab)^{12}\) is the shortest word in the generators of \(G\) which does not represent the identity in the free product of 3 cyclic groups of order 2, but which represents the identity in \(G\). However, the group \(G\) has elements of other finite orders as well -- for example:
gap> g := (b*a)^3*b*c;; Order(g);; gap> Display(g); Rcwa permutation of Z with modulus 36, of order 105 ( 8(9), 16(18), 64(72), 256(288), 85(96), 128(144), 32(36) ) ( 7(12), 11(18), 22(36) ) ( 5(18), 10(36), 40(144), 13(48), 20(72) ) ( 1(24), 2(36), 4(72) ) ( 14(36), 28(72), 112(288), 37(96), 56(144) ) gap> Order(a*c*b*a*b*c*a*c); 60
With some more efforts, one finds that e.g. \((abc)^2c^b\) has order 616, that \((abc)^2b\) has order 2310, that \((ab)^2a^ca^bc\) has order 27720, and that \(a(c(ab)^2)^2\) has order 65520. Of course \(G\) has many elements of infinite order as well. Some of them have infinite cycles, like e.g.
gap> g := b*c;; gap> Display(g); Rcwa permutation of Z with modulus 12 / | 4n if n in 1(3) | 2n if n in 5(6) n |-> < n/2 if n in 2(12) | n/4 if n in 8(12) | n if n in 0(3) \ gap> Sinks(g); [ 4(12) ] gap> Trajectory(g,last[1],10); [ 4(12), 16(48), 64(192), 256(768), 1024(3072), 4096(12288), 16384(49152), 65536(196608), 262144(786432), 1048576(3145728) ] gap> Trajectory(g,4,20); [ 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864, 268435456, 1073741824, 4294967296, 17179869184, 68719476736, 274877906944, 1099511627776 ]
Others seem to have only finite cycles. Some of these appear to have on average
comparatively short
cycles, like e.g.
gap> g := a*b*a*c*b*c; <rcwa permutation of Z with modulus 144> gap> cycs := ShortCycles(g,[0..10000],100,10^20);; gap> Difference([0..10000],Union(cycs)); [ ] gap> Collected(List(cycs,Length)); [ [ 1, 2222 ], [ 3, 1945 ], [ 4, 1111 ], [ 5, 93 ], [ 6, 926 ], [ 7, 31 ], [ 8, 864 ], [ 9, 10 ], [ 10, 289 ], [ 11, 4 ], [ 12, 95 ], [ 13, 1 ], [ 14, 31 ], [ 16, 12 ], [ 18, 4 ], [ 20, 1 ] ]
If the cycle of \(g\) containing some \(n \in ℤ\) is finite and has a certain length \(l\), then there is some \(m \in ℤ\) such that for every \(k \in ℤ\) the cycle of \(g\) containing \(n + km\) has length \(l\) as well. Thus, in other words, every finite cycle of \(g\) belongs to
a cycle of residue classes. (This is a special property of \(g\) which is not shared by every rcwa permutation -- cf. e.g. Collatz' permutation from Section 7.2.) We can find some of these infinitely many residue class cycles
:
gap> cycsrc := ShortResidueClassCycles(g,Mod(g),20); [ [ 0(6) ], [ 3(6), 160(288), 20(36) ], [ 7(18), 352(864), 44(108), 28(72) ], [ 11(18), 544(864), 2896(4608), 362(576), 68(108), 88(144) ], [ 13(18), 640(864), 80(108), 52(72) ], [ 10(36) ], [ 34(36) ], [ 1(54), 64(2592), 8(324), 4(216), 16(1152), 2(144) ], [ 5(54), 256(2592), 1360(13824), 170(1728), 32(324), 40(432), 208(2304), 26(288) ], [ 17(54), 832(2592), 4432(13824), 23632(73728), 2954(9216), 554(1728), 104(324), 136(432) ], [ 37(54), 1792(2592), 224(324), 148(216), 784(1152), 98(144) ], [ 41(54), 1984(2592), 10576(13824), 1322(1728), 248(324), 328(432), 1744(2304), 218(288) ], [ 53(54), 2560(2592), 13648(13824), 72784(73728), 9098(9216), 1706(1728), 320(324), 424(432) ], [ 38(72), 58(108), 304(576) ], [ 62(72), 94(108), 496(576) ] ] gap> List(cycsrc,Length); [ 1, 3, 4, 6, 4, 1, 1, 6, 8, 8, 6, 8, 8, 3, 3 ] gap> Sum(List(Flat(cycsrc),cl->1/Mod(cl))); 97459/110592 gap> Float(last); # about 88% 'coverage' 0.881248 gap> cycsrc := ShortResidueClassCycles(g,3*Mod(g),20); [ [ 0(6) ], [ 3(6), 160(288), 20(36) ], [ 7(18), 352(864), 44(108), 28(72) ], [ 11(18), 544(864), 2896(4608), 362(576), 68(108), 88(144) ], [ 13(18), 640(864), 80(108), 52(72) ], [ 10(36) ], [ 34(36) ], [ 1(54), 64(2592), 8(324), 4(216), 16(1152), 2(144) ], [ 5(54), 256(2592), 1360(13824), 170(1728), 32(324), 40(432), 208(2304), 26(288) ], [ 17(54), 832(2592), 4432(13824), 23632(73728), 2954(9216), 554(1728), 104(324), 136(432) ], [ 37(54), 1792(2592), 224(324), 148(216), 784(1152), 98(144) ], [ 41(54), 1984(2592), 10576(13824), 1322(1728), 248(324), 328(432), 1744(2304), 218(288) ], [ 53(54), 2560(2592), 13648(13824), 72784(73728), 9098(9216), 1706(1728), 320(324), 424(432) ], [ 38(72), 58(108), 304(576) ], [ 62(72), 94(108), 496(576) ], [ 23(162), 1120(7776), 5968(41472), 746(5184), 140(972), 184(1296), 976(6912), 5200(36864), 650(4608), 122(864) ], [ 35(162), 1696(7776), 9040(41472), 48208(221184), 257104(1179648), 32138(147456), 6026(27648), 1130(5184), 212(972), 280(1296) ], [ 73(162), 3520(7776), 440(972), 292(648), 1552(3456), 8272(18432), 1034(2304), 194(432) ], [ 77(162), 3712(7776), 19792(41472), 2474(5184), 464(972), 616(1296), 3280(6912), 17488(36864), 2186(4608), 410(864) ], [ 89(162), 4288(7776), 22864(41472), 121936(221184), 650320(1179648), 81290(147456), 15242(27648), 2858(5184), 536(972), 712(1296) ], [ 127(162), 6112(7776), 764(972), 508(648), 2704(3456), 14416(18432), 1802(2304), 338(432) ], [ 14(216), 22(324), 112(1728), 592(9216), 74(1152) ], [ 86(216), 130(324), 688(1728), 3664(9216), 458(1152) ] ] gap> List(cycsrc,Length); [ 1, 3, 4, 6, 4, 1, 1, 6, 8, 8, 6, 8, 8, 3, 3, 10, 10, 8, 10, 10, 8, 5, 5 ] gap> Sum(List(Flat(cycsrc),Density)); 5097073/5308416 gap> Float(last); # already about 96% 'coverage' 0.960187
There are also some elements of infinite order whose cycles seem to be all finite, but on average
pretty long
-- e.g.
gap> g := (b*a*c)^2*a;; gap> Display(g); Rcwa permutation of Z with modulus 288 / | (16n-1)/3 if n in 1(3) | (9n+5)/4 if n in 3(24) U 11(24) | (27n+19)/4 if n in 15(24) U 23(24) | (3n+1)/4 if n in 5(24) | (n-3)/6 if n in 21(24) | (27n+29)/8 if n in 9(48) U 41(48) | (9n+7)/8 if n in 17(48) U 33(48) | (2n-7)/9 if n in 8(36) n |-> < (4n-11)/9 if n in 32(36) | (27n+38)/8 if n in 14(48) | (3n+2)/8 if n in 26(48) | (9n+10)/8 if n in 38(48) | (3n+4)/4 if n in 20(72) | n/4 if n in 56(72) | (9n+14)/16 if n in 2(96) | (27n+58)/16 if n in 50(96) | n if n in 0(6) \ gap> List([1..100],n->Length(Cycle(g,n))); [ 6, 1, 6, 6, 6, 1, 194, 6, 216, 26, 26, 1, 26, 194, 65, 26, 26, 1, 216, 26, 6, 216, 46, 1, 640, 26, 70, 194, 216, 1, 70, 26, 216, 216, 26, 1, 194, 216, 73, 26, 110, 1, 194, 216, 194, 111, 39, 1, 194, 640, 640, 194, 26, 1, 171, 194, 204, 640, 216, 1, 111, 70, 91, 26, 194, 1, 216, 216, 26, 111, 65, 1, 50, 194, 26, 216, 640, 1, 502, 26, 111, 40, 110, 1, 26, 194, 385, 640, 88, 1, 100, 111, 65, 110, 416, 1, 171, 194, 194, 640 ] gap> Length(Cycle(g,25)); 640 gap> Maximum(Cycle(g,25)); 323270249684063829 gap> Length(Cycle(g,25855)); 4751 gap> Maximum(Cycle(g,25855)); 507359605810239426786254778159924369135184044618585904603866210104085 gap> cycs := ShortCycles(g,[0..50000],10000,10^100);; gap> S := [0..50000];; gap> for cyc in cycs do S := Difference(S,cyc); od; gap> S; # no cycle containing some n in [0..50000] has length > 10000 [ ]
Taking a look at the lengths of the trajectories of the Collatz mapping \(T\) starting at the points in a cycle, we can see how a cycle of \(g\) goes up and down
in the \(3n+1\) tree:
gap> List(Cycle(g,25),n->Length(Trajectory(T,n,[1]))); [ 17, 21, 25, 29, 33, 31, 35, 34, 32, 33, 37, 41, 45, 44, 42, 39, 43, 41, 45, 44, 42, 43, 40, 38, 35, 39, 37, 41, 40, 44, 48, 46, 50, 49, 47, 48, 45, 42, 46, 44, 48, 47, 45, 46, 50, 49, 47, 43, 41, 38, 39, 36, 34, 30, 27, 31, 29, 33, 32, 30, 31, 35, 33, 37, 36, 40, 39, 43, 41, 45, 44, 42, 43, 47, 51, 55, 53, 57, 56, 54, 55, 59, 58, 62, 66, 64, 68, 67, 65, 66, 63, 60, 64, 62, 66, 65, 63, 64, 68, 67, 65, 61, 59, 56, 52, 49, 53, 51, 55, 54, 52, 53, 57, 55, 59, 58, 56, 57, 54, 50, 48, 45, 49, 47, 51, 50, 54, 52, 56, 55, 53, 54, 58, 62, 66, 70, 74, 72, 76, 75, 79, 83, 87, 91, 90, 94, 93, 97, 95, 99, 98, 96, 97, 94, 91, 88, 85, 89, 87, 91, 90, 88, 89, 86, 84, 81, 85, 83, 87, 86, 90, 94, 98, 97, 101, 105, 109, 107, 111, 110, 108, 109, 113, 117, 115, 119, 118, 122, 126, 125, 123, 120, 124, 122, 126, 125, 123, 124, 121, 119, 116, 117, 114, 111, 115, 113, 117, 116, 114, 115, 119, 123, 122, 120, 117, 121, 119, 123, 122, 120, 121, 118, 116, 112, 110, 106, 103, 107, 105, 109, 108, 106, 107, 111, 109, 113, 112, 116, 114, 118, 117, 115, 116, 113, 110, 111, 108, 104, 102, 99, 103, 101, 105, 104, 108, 106, 110, 109, 107, 108, 112, 111, 109, 105, 102, 103, 100, 98, 95, 92, 96, 94, 98, 97, 95, 96, 93, 91, 88, 92, 90, 94, 93, 97, 101, 105, 109, 108, 106, 103, 107, 105, 109, 108, 106, 107, 104, 102, 99, 103, 101, 105, 104, 108, 112, 110, 114, 113, 111, 112, 116, 115, 113, 109, 106, 110, 108, 112, 111, 109, 110, 114, 112, 116, 115, 113, 114, 111, 107, 105, 102, 103, 100, 98, 95, 99, 97, 101, 100, 104, 103, 107, 105, 109, 108, 106, 107, 104, 101, 98, 99, 96, 94, 91, 92, 89, 87, 84, 85, 82, 80, 77, 81, 79, 83, 82, 86, 85, 89, 88, 86, 83, 80, 81, 78, 76, 73, 74, 71, 68, 72, 70, 74, 73, 71, 72, 76, 80, 79, 83, 87, 91, 90, 88, 85, 89, 87, 91, 90, 88, 89, 86, 84, 81, 85, 83, 87, 86, 90, 94, 92, 96, 95, 93, 94, 98, 96, 100, 99, 97, 98, 102, 106, 110, 114, 113, 111, 108, 112, 110, 114, 113, 111, 112, 109, 107, 104, 108, 106, 110, 109, 113, 117, 115, 119, 118, 116, 117, 114, 111, 115, 113, 117, 116, 114, 115, 119, 118, 116, 112, 110, 107, 108, 105, 103, 100, 104, 102, 106, 105, 109, 108, 112, 110, 114, 113, 111, 112, 116, 115, 113, 109, 106, 103, 104, 101, 99, 95, 91, 88, 92, 90, 94, 93, 91, 92, 96, 94, 98, 97, 95, 96, 100, 98, 102, 101, 105, 104, 102, 99, 100, 97, 93, 89, 87, 84, 85, 82, 80, 77, 74, 78, 76, 80, 79, 77, 78, 75, 73, 69, 67, 64, 68, 66, 70, 69, 73, 71, 75, 74, 72, 73, 70, 67, 68, 65, 63, 60, 64, 62, 66, 65, 69, 68, 66, 63, 64, 61, 59, 56, 60, 58, 62, 61, 65, 64, 62, 59, 60, 57, 55, 51, 48, 49, 46, 44, 40, 37, 34, 35, 32, 28, 26, 23, 27, 25, 29, 28, 32, 30, 34, 33, 31, 32, 36, 35, 33, 29, 26, 27, 24, 22, 19, 23, 21, 25, 24, 28, 27, 25, 22, 23, 20, 18, 14, 18, 22, 20, 24, 23, 21, 22, 19, 16, 20, 18, 22, 21, 19, 20, 24, 23, 21, 17, 15, 17, 15, 19, 18, 16 ] gap> lngs := List(Cycle(g,25855),n->Length(Trajectory(T,n,[1])));; gap> Minimum(lngs); 55 gap> Maximum(lngs); 521 gap> Position(lngs,55); 15 gap> Position(lngs,521); 2807
Finally let's have a look at elements of \(G\) with small modulus:
gap> B := RestrictedBall(G,One(G),20,36:Spheres);; gap> List(B,Length); [ 1, 3, 6, 12, 4, 6, 6, 4, 4, 4, 6, 6, 3, 3, 2, 0, 0, 0, 0, 0, 0 ] gap> Sum(last); 70 gap> Position(last2,0)-2; 14
So we have 70 elements of modulus 36 or less in \(G\) which can be reached from the identity by successive multiplication with generators without passing elements with mudulus exceeding 36. Further we see that the longest word in the generators yielding an element with modulus at most 36 has length 14. Now we double our bound on the modulus:
gap> B := RestrictedBall(G,One(G),100,72:Spheres);; gap> List(B,Length); [ 1, 3, 6, 12, 22, 14, 18, 22, 24, 26, 26, 34, 35, 32, 37, 38, 46, 58, 65, 73, 82, 91, 93, 96, 110, 121, 114, 117, 146, 138, 148, 168, 174, 196, 215, 214, 232, 255, 280, 305, 315, 359, 377, 371, 363, 366, 397, 419, 401, 405, 405, 401, 407, 415, 435, 424, 401, 359, 338, 330, 332, 281, 278, 271, 269, 254, 255, 257, 258, 258, 233, 215, 202, 185, 154, 121, 88, 55, 35, 20, 10, 5, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ] gap> Sum(last); 15614 gap> Position(last2,0)-2; 83 gap> Collected(List(Flat(B),Modulus)); [ [ 1, 1 ], [ 6, 3 ], [ 12, 4 ], [ 18, 2 ], [ 24, 4 ], [ 36, 56 ], [ 48, 4 ], [ 72, 15540 ] ]
We observe that there are 15540 elements in \(G\) with modulus 72 which are reachable
from the identity by successive multiplication with generators without passing elements with mudulus exceeding 72. Further we see that the longest word in the generators yielding an element with modulus at most 72 has length 83.
It is obvious that many questions regarding the group \(G\) remain open.
In this section we investigate a group which has huge finite orbits on ℤ.
gap> a := ClassTransposition(0,2,1,2);; gap> b := ClassTransposition(0,5,4,5);; gap> c := ClassTransposition(1,4,0,6);; gap> G := Group(a,b,c); <(0(2),1(2)),(0(5),4(5)),(1(4),0(6))> gap> LoadDatabaseOfGroupsGeneratedBy3ClassTranspositions(); "3CTsGroups6" gap> 3CTsGroups6.Id3CTsGroup(G,3CTsGroups6.grps); # 'catalogue number' of G 1284
We look for orbits of length at most 100 containing an integer in the range [0..1000]:
gap> orbs := ShortOrbits(G,[0..1000],100);; gap> List(orbs,Length); [ 16, 2, 24, 2, 2, 2, 8, 2, 8, 2, 2, 8, 2, 8, 2, 2, 2, 40, 2, 8, 24, 2, 8, 2, 2, 8, 2, 24, 8, 2, 56, 2, 2, 2, 8, 2, 8, 2, 2, 8, 2, 8, 2, 2, 2, 24, 2, 8, 2, 8, 2, 2, 8, 2, 8, 2, 24, 2, 2, 2, 8, 2, 8, 2, 2, 8, 2, 8, 2, 2, 2, 2, 8, 24, 2, 8, 2, 2, 8, 2, 24, 8, 2, 2, 2, 2, 8, 2, 8, 2, 2, 8, 2, 8, 2, 2, 2, 24, 2, 8, 2, 8, 2, 2, 8, 2, 8, 2, 24, 2, 2 ] gap> Collected(last); [ [ 2, 67 ], [ 8, 32 ], [ 16, 1 ], [ 24, 9 ], [ 40, 1 ], [ 56, 1 ] ] gap> Length(Difference([0..1000],Union(orbs))); 491
So almost half of the integers in the range [0..1000] lie in orbits of length larger than 100. In fact there are much larger orbits. For example:
gap> B := Ball(G,32,500,OnPoints:Spheres);; # compute ball about 32 gap> Position(B,[]); # <> fail -> we have exhausted the orbit 354 gap> Sum(List(B,Length)); # the orbit length 6296 gap> Maximum(Flat(B)); # the largest integer in the orbit 3301636381609509797437679 gap> B := Ball(G,736,5000,OnPoints:Spheres);; # the same for 736 ... gap> Position(B,[]); 2997 gap> Sum(List(B,Length)); # the orbit length for this time 495448 gap> Maximum(Flat(B)); 2461374276522713949036151811903149785690151467356354652860276957152301465\ 0546360696627187194849439881973442451686685024708652634593861146709752378\ 847078493406287854573381920553713155967741550498839
It seems that the cycles of \(abc\) completely traverse all orbits of \(G\), with the only exception of the orbit of 0. Let's check this in the above examples:
gap> g := a*b*c;; gap> Display(g); Rcwa permutation of Z with modulus 60 / | n-1 if n in 3(30) U 9(30) U 17(30) U 23(30) U 27(30) U | 29(30) | 3n/2 if n in 0(20) U 12(20) U 16(20) | n+1 if n in 2(20) U 6(20) U 10(20) | (2n+1)/3 if n in 7(30) U 13(30) U 19(30) | n+3 if n in 1(30) U 11(30) n |-> < n-5 if n in 15(30) U 25(30) | (3n+12)/2 if n in 4(20) | (3n-12)/2 if n in 8(20) | n+5 if n in 14(20) | n-3 if n in 18(20) | (2n-7)/3 if n in 5(30) | (2n+9)/3 if n in 21(30) \ gap> Length(Cycle(g,32)); 6296 gap> Length(Cycle(g,736)); 495448
Representatives and lengths of the cycles of \(g\) which intersect nontrivially with the range [0..1000] are as follows:
gap> CycleRepresentativesAndLengths(g,[0..1000]:notify:=50000); n = 736: after 50000 steps, the iterate has 157 binary digits. n = 736: after 100000 steps, the iterate has 135 binary digits. n = 736: after 150000 steps, the iterate has 131 binary digits. n = 736: after 200000 steps, the iterate has 507 binary digits. n = 736: after 250000 steps, the iterate has 414 binary digits. n = 736: after 300000 steps, the iterate has 457 binary digits. n = 736: after 350000 steps, the iterate has 465 binary digits. n = 736: after 400000 steps, the iterate has 325 binary digits. n = 736: after 450000 steps, the iterate has 534 binary digits. n = 896: after 50000 steps, the iterate has 359 binary digits. n = 896: after 100000 steps, the iterate has 206 binary digits. [ [ 1, 15 ], [ 2, 2 ], [ 16, 24 ], [ 22, 2 ], [ 26, 2 ], [ 32, 6296 ], [ 46, 2 ], [ 52, 8 ], [ 56, 296 ], [ 62, 2 ], [ 76, 8 ], [ 82, 2 ], [ 86, 2 ], [ 92, 8 ], [ 106, 2 ], [ 112, 104 ], [ 116, 8 ], [ 122, 2 ], [ 136, 440 ], [ 142, 2 ], [ 146, 2 ], [ 152, 40 ], [ 166, 2 ], [ 172, 8 ], [ 176, 24 ], [ 182, 2 ], [ 196, 8 ], [ 202, 2 ], [ 206, 2 ], [ 212, 8 ], [ 226, 2 ], [ 232, 24 ], [ 236, 8 ], [ 242, 2 ], [ 256, 56 ], [ 262, 2 ], [ 266, 2 ], [ 272, 408 ], [ 286, 2 ], [ 292, 8 ], [ 296, 104 ], [ 302, 2 ], [ 316, 8 ], [ 322, 2 ], [ 326, 2 ], [ 332, 8 ], [ 346, 2 ], [ 352, 264 ], [ 356, 8 ], [ 362, 2 ], [ 376, 1304 ], [ 382, 2 ], [ 386, 2 ], [ 392, 24 ], [ 406, 2 ], [ 412, 8 ], [ 416, 200 ], [ 422, 2 ], [ 436, 8 ], [ 442, 2 ], [ 446, 2 ], [ 452, 8 ], [ 466, 2 ], [ 472, 104 ], [ 476, 8 ], [ 482, 2 ], [ 496, 24 ], [ 502, 2 ], [ 506, 2 ], [ 512, 696 ], [ 526, 2 ], [ 532, 8 ], [ 536, 3912 ], [ 542, 2 ], [ 556, 8 ], [ 562, 2 ], [ 566, 2 ], [ 572, 8 ], [ 586, 2 ], [ 592, 888 ], [ 596, 8 ], [ 602, 2 ], [ 616, 728 ], [ 622, 2 ], [ 626, 2 ], [ 632, 2776 ], [ 646, 2 ], [ 652, 8 ], [ 656, 24 ], [ 662, 2 ], [ 676, 8 ], [ 682, 2 ], [ 686, 2 ], [ 692, 8 ], [ 706, 2 ], [ 712, 24 ], [ 716, 8 ], [ 722, 2 ], [ 736, 495448 ], [ 742, 2 ], [ 746, 2 ], [ 752, 1272 ], [ 766, 2 ], [ 772, 8 ], [ 776, 376 ], [ 782, 2 ], [ 796, 8 ], [ 802, 2 ], [ 806, 2 ], [ 812, 8 ], [ 826, 2 ], [ 832, 120 ], [ 836, 8 ], [ 842, 2 ], [ 856, 2264 ], [ 862, 2 ], [ 866, 2 ], [ 872, 24 ], [ 886, 2 ], [ 892, 8 ], [ 896, 132760 ], [ 902, 2 ], [ 916, 8 ], [ 922, 2 ], [ 926, 2 ], [ 932, 8 ], [ 946, 2 ], [ 952, 456 ], [ 956, 8 ], [ 962, 2 ], [ 976, 24 ], [ 982, 2 ], [ 986, 2 ], [ 992, 1064 ] ]
So far the author has checked that all positive integers less than 173176 lie in finite cycles of \(g\). Several of them are longer than 1000000, and the cycle containing 25952 has length 245719352. Whether the cycle containing 173176 is finite or infinite has not been checked so far -- in any case it is longer than 5700000000, and it exceeds \(10^{40000}\). Presumably it is finite as well, but checking this may require a lot of computing time.
On the one hand the cycles of \(g\) seem to behave randomly
, perhaps as if they would ascend or descend from one point to the next by a certain factor depending on which side a thrown coin falls on. -- In this model
, cycles would be finite with probability 1 since the simple random walk on ℤ is recurrent. On the other, there seems to be quite some structure on them, however little is known so far.
First we observe that each orbit under the action of \(G\) seems to split into two cycles of \(h := abcacb\) of the same length (of course this has been checked for many more orbits than those shown here):
gap> h := a*b*c*a*c*b; <rcwa permutation of Z with modulus 360> gap> List(CyclesOnFiniteOrbit(G,h,32),Length); [ 3148, 3148 ] gap> List(CyclesOnFiniteOrbit(G,h,736),Length); [ 247724, 247724 ]
One cycle seems to contain the points at the odd positions and the other seems to contain the points at the even positions in the cycle of \(g\):
gap> cycle_g := Cycle(g,32);; gap> positions1 := List(Cycle(h,32),n->Position(cycle_g,n));; gap> Collected(positions1 mod 2); [ [ 1, 3148 ] ] gap> positions2 := List(Cycle(h,33),n->Position(cycle_g,n));; gap> Collected(positions2 mod 2); [ [ 0, 3148 ] ]
However the ordering in which these points are traversed looks pretty scrambled
:
gap> positions1{[1..200]}; [ 1, 6271, 6291, 6281, 6285, 6287, 6283, 6289, 6273, 6275, 6277, 6279, 6293, 5, 15, 17, 19, 6259, 6261, 6263, 6265, 21, 23, 25, 41, 6227, 6229, 6231, 6233, 6235, 6237, 6239, 43, 53, 55, 57, 63, 59, 61, 65, 45, 47, 49, 51, 67, 6223, 6221, 69, 6163, 6215, 6205, 6209, 6211, 6207, 6213, 6165, 6171, 6177, 6179, 6181, 6183, 6175, 6173, 6185, 6189, 6191, 6187, 6193, 6169, 6167, 6195, 6199, 6201, 6197, 6203, 6217, 73, 83, 85, 87, 103, 113, 115, 117, 4357, 4361, 4363, 4359, 4365, 4371, 4373, 4375, 4377, 4369, 4367, 4379, 119, 121, 123, 125, 129, 131, 127, 133, 139, 141, 143, 145, 137, 135, 147, 149, 151, 153, 155, 159, 161, 157, 163, 169, 175, 4283, 4281, 177, 4271, 4273, 4275, 4277, 181, 4255, 4257, 4259, 4261, 4263, 4265, 4267, 183, 2161, 2163, 4195, 4199, 4201, 4197, 4203, 4209, 4211, 4213, 4215, 4207, 4205, 4217, 2165, 2167, 2169, 2171, 2175, 2177, 2173, 2179, 2185, 2187, 2189, 2191, 2183, 2181, 2193, 2195, 2197, 2199, 2201, 2467, 2469, 4117, 4121, 4123, 4119, 4125, 4131, 4133, 4135, 4137, 4129, 4127, 4139, 2471, 2473, 2475, 2477, 2487, 2489, 2491, 2507, 2517, 2519, 2521, 2537, 3923, 3925, 3941, 3943 ]
In this section, we would like to show that the group \(G\) generated by the two permutations
gap> a := RcwaMapping([[3,0,2],[3,1,4],[3,0,2],[3,-1,4]]);; gap> u := RcwaMapping([[3,0,5],[9,1,5],[3,-1,5],[9,-2,5],[9,4,5]]);; gap> SetName(a,"a"); SetName(u,"u"); G := Group(a,u);;
which we have already investigated in earlier examples acts 4-transitively on the set of positive integers. Obviously, it acts on the set of positive integers. First we show that this action is transitive. We start by checking in which residue classes sufficiently large positive integers are mapped to smaller ones by a suitable group element:
gap> List([a,a^-1,u,u^-1],DecreasingOn); [ 1(2), 0(3), 0(5) U 2(5), 2(3) ] gap> Union(last); Z \ 4(30) U 16(30) U 28(30)
We see that we cannot always choose such a group element from the set of generators and their inverses -- otherwise the union would be Integers.
gap> List([a,a^-1,u,u^-1,a^2,a^-2,u^2,u^-2],DecreasingOn); [ 1(2), 0(3), 0(5) U 2(5), 2(3), 1(8) U 7(8), 0(3) U 2(9) U 7(9), 0(25) U 12(25) U 17(25) U 20(25), 2(3) U 1(9) U 3(9) ] gap> Union(last); # Still not enough ... Z \ 4(90) U 58(90) U 76(90) gap> List([a,a^-1,u,u^-1,a^2,a^-2,u^2,u^-2,a*u,u*a,(a*u)^-1,(u*a)^-1], > DecreasingOn); [ 1(2), 0(3), 0(5) U 2(5), 2(3), 1(8) U 7(8), 0(3) U 2(9) U 7(9), 0(25) U 12(25) U 17(25) U 20(25), 2(3) U 1(9) U 3(9), 3(5) U 0(10) U 7(20) U 9(20), 0(5) U 2(5), 2(3), 3(9) U 4(9) U 8(9) ] gap> Union(last); # ... but that's it! Integers
Finally, we have to deal with small
integers. We use the notation for the coefficients of rcwa mappings introduced at the beginning of this manual. Let \(c_{r(m)} > a_{r(m)}\). Then we easily see that \((a_{r(m)}n+b_{r(m)})/c_{r(m)} > n\) implies \(n < b_{r(m)}/(c_{r(m)}-a_{r(m)})\). Thus we can restrict our considerations to integers \(n < b_{\rm max}\), where \(b_{\rm max}\) is the largest second entry of a coefficient triple of one of the group elements in our list:
gap> List([a,a^-1,u,u^-1,a^2,a^-2,u^2,u^-2,a*u,u*a,(a*u)^-1,(u*a)^-1], > f->Maximum(List(Coefficients(f),c->c[2]))); [ 1, 1, 4, 2, 7, 7, 56, 28, 25, 17, 17, 11 ] gap> Maximum(last); 56
Thus this upper bound is 56. The rest is easy -- all we have to do is to check that the orbit containing 1 contains also all other positive integers less than or equal to 56:
gap> S := [1];; gap> while not IsSubset(S,[1..56]) do > S := Union(S,S^a,S^u,S^(a^-1),S^(u^-1)); > od; gap> IsSubset(S,[1..56]); true
Checking 2-transitivity is computationally harder, and in the sequel we will omit some steps which are in practice needed to find out what to do
. The approach taken here is to show that the stabilizer of 1 in \(G\) acts transitively on the set of positive integers greater than 1. We do this by similar means as used above for showing the transitivity of the action of \(G\) on the positive integers. We start by determining all products of at most 5 generators and their inverses, which stabilize 1 (taking at most 4-generator products would not suffice!):
gap> gens := [a,u,a^-1,u^-1];; gap> tups := Concatenation(List([1..5],k->Tuples([1..4],k)));; gap> Length(tups); 1364 gap> tups := Filtered(tups,tup->ForAll([[1,3],[3,1],[2,4],[4,2]], > l->PositionSublist(tup,l)=fail));; gap> Length(tups); 484 gap> stab := [];; gap> for tup in tups do > n := 1; > for i in tup do n := n^gens[i]; od; > if n = 1 then Add(stab,tup); fi; > od; gap> Length(stab); 118 gap> stabelm := List(stab,tup->Product(List(tup,i->gens[i])));; gap> ForAll(stabelm,elm->1^elm=1); # Check. true
The resulting products have various different not quite small moduli:
gap> List(stabelm,Modulus); [ 4, 3, 16, 25, 9, 81, 64, 100, 108, 100, 25, 75, 27, 243, 324, 243, 256, 400, 144, 400, 100, 432, 324, 400, 80, 400, 625, 25, 75, 135, 150, 75, 225, 81, 729, 486, 729, 144, 144, 81, 729, 1296, 729, 6561, 1024, 1600, 192, 1600, 400, 576, 432, 1600, 320, 1600, 2500, 100, 100, 180, 192, 192, 108, 972, 1728, 972, 8748, 1600, 400, 320, 80, 1600, 2500, 300, 2500, 625, 625, 75, 675, 75, 75, 135, 405, 600, 120, 600, 1875, 75, 225, 405, 225, 225, 675, 243, 2187, 729, 2187, 216, 216, 243, 2187, 1944, 2187, 19683, 576, 144, 576, 432, 81, 81, 729, 2187, 5184, 324, 8748, 243, 2187, 19683, 26244, 19683 ] gap> Lcm(last); 12597120000 gap> Collected(Factors(last)); [ [ 2, 10 ], [ 3, 9 ], [ 5, 4 ] ]
Similar as before, we determine for any of the above mappings the residue classes whose elements larger than the largest \(b_{r(m)}\) - coefficient of the respective mapping are mapped to smaller integers:
gap> decs := List(stabelm,DecreasingOn);; gap> List(decs,Modulus); [ 2, 3, 8, 25, 9, 9, 16, 100, 12, 50, 25, 75, 27, 81, 54, 81, 64, 400, 48, 200, 100, 72, 108, 400, 80, 200, 625, 25, 75, 45, 75, 75, 225, 81, 243, 81, 243, 144, 144, 81, 243, 216, 243, 243, 128, 1600, 64, 400, 400, 48, 144, 1600, 320, 400, 2500, 100, 100, 60, 96, 192, 108, 324, 144, 324, 972, 400, 400, 80, 80, 400, 2500, 100, 1250, 625, 625, 25, 75, 75, 75, 45, 135, 600, 120, 150, 1875, 75, 225, 135, 225, 225, 675, 243, 729, 243, 729, 108, 216, 243, 729, 162, 729, 2187, 144, 144, 144, 144, 81, 81, 243, 729, 1296, 324, 972, 243, 729, 2187, 1458, 2187 ] gap> Lcm(last); 174960000
Since the least common multiple of the moduli of these unions of residue classes is as large as 174960000, directly forming their union and checking whether it is equal to the set of integers would take relatively much time and memory. However, starting with the set of integers and subtracting the above sets one-by-one in a suitably chosen order is cheap:
gap> SortParallel(decs,stabelm, > function(S1,S2) > return First([1..100],k->Factorial(k) mod Modulus(S1)=0) > < First([1..100],k->Factorial(k) mod Modulus(S2)=0); > end); gap> S := Integers;; gap> for i in [1..Length(decs)] do > S_old := S; S := Difference(S,decs[i]); > if S <> S_old then ViewObj(S); Print("\n"); fi; > if S = [] then maxind := i; break; fi; > od; 0(2) 2(6) U 4(6) <union of 19 residue classes (mod 60) (6 classes)> <union of 8 residue classes (mod 30)> <union of 120 residue classes (mod 720)> <union of 112 residue classes (mod 720)> <union of 80 residue classes (mod 720)> <union of 24 residue classes (mod 720)> <union of 16 residue classes (mod 720) (12 classes)> <union of 8 residue classes (mod 720)> <union of 6 residue classes (mod 720)> 4(720) U 94(720) U 148(720) U 238(720) <union of 24 residue classes (mod 5760)> <union of 72 residue classes (mod 51840)> <union of 48 residue classes (mod 51840)> <union of 204 residue classes (mod 259200)> <union of 144 residue classes (mod 259200)> <union of 120 residue classes (mod 259200)> <union of 84 residue classes (mod 259200)> <union of 72 residue classes (mod 259200)> <union of 48 residue classes (mod 259200)> <union of 24 residue classes (mod 259200)> <union of 12 residue classes (mod 259200) (6 classes)> <union of 30 residue classes (mod 777600)> 54004(64800) U 151204(259200) U 216004(259200) [ ]
Similar as above, it remains to check that the small
integers all lie in the orbit containing 2. Obviously, it is sufficient to check that any integer greater than 2 is mapped to a smaller one by some suitably chosen element of the stabilizer under consideration:
gap> Maximum(List(stabelm{[1..maxind]}, > f->Maximum(List(Coefficients(f),c->c[2])))); 6581 gap> Filtered([3..6581],n->Minimum(List(stabelm,elm->n^elm))>=n); [ 4 ]
We have to treat 4 separately:
gap> 1^(u*a*u^2*a^-1*u); 1 gap> 4^(u*a*u^2*a^-1*u); 3
Now we know that any positive integer greater than 1 lies in the same orbit under the action of the stabilizer of 1 in \(G\) as 2, thus that this stabilizer acts transitively on \(ℕ \setminus \{1\}\). But this means that we have established the 2-transitivity of the action of \(G\) on ℕ.
In the following, we essentially repeat the above steps to show that this action is indeed 3-transitive:
gap> tups := Concatenation(List([1..6],k->Tuples([1..4],k)));; gap> tups := Filtered(tups,tup->ForAll([[1,3],[3,1],[2,4],[4,2]], > l->PositionSublist(tup,l)=fail));; gap> stab := [];; gap> for tup in tups do > l := [1,2]; > for i in tup do l := List(l,n->n^gens[i]); od; > if l = [1,2] then Add(stab,tup); fi; > od; gap> Length(stab); 212 gap> stabelm := List(stab,tup->Product(List(tup,i->gens[i])));; gap> decs := List(stabelm,DecreasingOn);; gap> SortParallel(decs,stabelm,function(S1,S2) > return First([1..100],k->Factorial(k) mod Mod(S1)=0) > < First([1..100],k->Factorial(k) mod Mod(S2)=0); end); gap> S := Integers;; gap> for i in [1..Length(decs)] do > S_old := S; S := Difference(S,decs[i]); > if S <> S_old then ViewObj(S); Print("\n"); fi; > if S = [] then break; fi; > od; Z \ 1(8) U 7(8) <union of 424 residue classes (mod 720)> <union of 169 residue classes (mod 720)> <union of 51 residue classes (mod 720)> <union of 45 residue classes (mod 720)> <union of 42 residue classes (mod 720)> <union of 35 residue classes (mod 720)> <union of 30 residue classes (mod 720)> <union of 16 residue classes (mod 720) (10 classes)> <union of 11 residue classes (mod 720) (7 classes)> <union of 8 residue classes (mod 720) (6 classes)> 148(360) U 238(360) U 4(720) U 454(720) 238(360) U 4(720) U 148(720) U 454(720) <union of 28 residue classes (mod 5760)> <union of 24 residue classes (mod 5760)> <union of 23 residue classes (mod 5760)> <union of 22 residue classes (mod 5760)> <union of 20 residue classes (mod 5760) (14 classes)> <union of 19 residue classes (mod 5760) (14 classes)> <union of 16 residue classes (mod 5760) (12 classes)> <union of 112 residue classes (mod 51840)> <union of 96 residue classes (mod 51840)> <union of 90 residue classes (mod 51840)> <union of 51 residue classes (mod 51840)> <union of 21 residue classes (mod 51840)> <union of 19 residue classes (mod 51840) (15 classes)> <union of 16 residue classes (mod 51840) (12 classes)> <union of 54 residue classes (mod 259200)> <union of 53 residue classes (mod 259200)> <union of 50 residue classes (mod 259200)> <union of 38 residue classes (mod 259200)> <union of 35 residue classes (mod 259200)> <union of 32 residue classes (mod 259200)> <union of 24 residue classes (mod 259200)> <union of 22 residue classes (mod 259200)> <union of 20 residue classes (mod 259200) (16 classes)> <union of 18 residue classes (mod 259200) (15 classes)> <union of 16 residue classes (mod 259200) (13 classes)> <union of 15 residue classes (mod 259200) (12 classes)> <union of 12 residue classes (mod 259200) (10 classes)> <union of 7 residue classes (mod 259200)> 2164(259200) U 66964(259200) U 228964(259200) [ ] gap> Maximum(List(stabelm,f->Maximum(List(Coefficients(f),c->c[2])))); 515816 gap> smallnum := [4..515816];; gap> for i in [1..Length(stabelm)] do > smallnum := Filtered(smallnum,n->n^stabelm[i]>=n); > od; gap> smallnum; [ ]
The same for 4-transitivity:
gap> tups := Concatenation(List([1..8],k->Tuples([1..4],k)));; gap> tups := Filtered(tups,tup->ForAll([[1,3],[3,1],[2,4],[4,2]], > l->PositionSublist(tup,l)=fail));; gap> stab := [];; gap> for tup in tups do > l := [1,2,3]; > for i in tup do l := List(l,n->n^gens[i]); od; > if l = [1,2,3] then Add(stab,tup); fi; > od; gap> Length(stab); 528 gap> stabelm := [];; gap> for i in [1..Length(stab)] do > elm := One(G); > for j in stab[i] do > if Modulus(elm) > 10000 then elm := fail; break; fi; > elm := elm * gens[j]; > od; > if elm <> fail then Add(stabelm,elm); fi; > od; gap> Length(stabelm); 334 gap> decs := List(stabelm,DecreasingOn);; gap> SortParallel(decs,stabelm, > function(S1,S2) > return First([1..100],k->Factorial(k) mod Modulus(S1) = 0) > < First([1..100],k->Factorial(k) mod Modulus(S2) = 0); > end); gap> S := Integers;; gap> for i in [1..Length(decs)] do > S_old := S; S := Difference(S,decs[i]); > if S <> S_old then ViewObj(S); Print("\n"); fi; > if S = [] then maxind := i; break; fi; > od; Z \ 1(8) U 7(8) <union of 24 residue classes (mod 72)> <union of 22 residue classes (mod 72)> <union of 17 residue classes (mod 72) (9 classes)> 4(18) <union of 28 residue classes (mod 576)> <union of 26 residue classes (mod 576)> <union of 21 residue classes (mod 576)> <union of 20 residue classes (mod 576) (7 classes)> <union of 18 residue classes (mod 576) (8 classes)> <union of 16 residue classes (mod 576) (6 classes)> <union of 15 residue classes (mod 576) (6 classes)> <union of 120 residue classes (mod 5184)> <union of 45 residue classes (mod 5184)> <union of 30 residue classes (mod 5184)> <union of 28 residue classes (mod 5184)> <union of 6 residue classes (mod 1296)> <union of 116 residue classes (mod 32400)> <union of 104 residue classes (mod 32400)> <union of 92 residue classes (mod 32400)> <union of 84 residue classes (mod 32400)> <union of 80 residue classes (mod 32400)> <union of 210 residue classes (mod 129600)> <union of 189 residue classes (mod 129600)> <union of 160 residue classes (mod 129600)> <union of 136 residue classes (mod 129600)> <union of 133 residue classes (mod 129600)> <union of 122 residue classes (mod 129600)> <union of 114 residue classes (mod 129600)> <union of 106 residue classes (mod 129600)> <union of 104 residue classes (mod 129600)> <union of 100 residue classes (mod 129600)> <union of 96 residue classes (mod 129600)> <union of 60 residue classes (mod 129600)> <union of 52 residue classes (mod 129600)> <union of 48 residue classes (mod 129600)> <union of 40 residue classes (mod 129600)> <union of 36 residue classes (mod 129600)> <union of 32 residue classes (mod 129600)> <union of 24 residue classes (mod 129600)> <union of 16 residue classes (mod 129600) (10 classes)> <union of 12 residue classes (mod 129600)> <union of 10 residue classes (mod 129600)> <union of 8 residue classes (mod 129600)> <union of 6 residue classes (mod 129600)> 57406(129600) U 63076(129600) U 115006(129600) U 120676(129600) 57406(129600) U 115006(129600) U 192676(259200) U 250276(259200) <union of 15 residue classes (mod 777600) (6 classes)> <union of 9 residue classes (mod 777600) (6 classes)> <union of 30 residue classes (mod 3110400)> <union of 26 residue classes (mod 3110400)> <union of 22 residue classes (mod 3110400)> <union of 19 residue classes (mod 3110400) (10 classes)> <union of 14 residue classes (mod 3110400) (8 classes)> 705406(777600) U 2007076(3110400) U 2649406(3110400) U 2784676(3110400) <union of 14 residue classes (mod 9331200) (8 classes)> 1483006(2332800) U 2649406(9331200) U 2784676(9331200) U 5117476(9331200) <union of 16 residue classes (mod 27993600) (6 classes)> 2784676(9331200) U 5117476(9331200) [ ] gap> Maximum(List(stabelm{[1..maxind]}, > f->Maximum(List(Coefficients(f),c->c[2])))); 37387 gap> smallnum := [5..37387];; gap> for i in [1..maxind] do > smallnum := Filtered(smallnum,n->n^stabelm[i]>=n); > od; gap> smallnum; [ ]
There is even some evidence that the degree of transitivity of the action of \(G\) on the positive integers is higher than 4:
gap> phi := EpimorphismFromFreeGroup(G); [ a, u ] -> [ a, u ] gap> F := Source(phi); <free group on the generators [ a, u ]> gap> List([5..20], > n->RepresentativeActionPreImage(G,[1,2,3,4,5], > [1,2,3,4,n],OnTuples,F)); [ <identity ...>, a^-3*u^4*a*u^-2*a^2, a^-1*(a^-1*u)^4*a^-1*u^-1*a, a^4*u^-2*a^-4, a^-1*u^-4*a, (u^2*a^-1)^2*u^-2, u^-2*a^-2*u^4, a^-1*u^2*a, a^-1*u^-6*a, a^2*u^4*a^2*u^2, u^-4*a*u^-2*a^-3, a^-1*u^-2*a^-3*u^4*a^2, a^2*(a*u^2)^2, (a*u^-4)^2*a^-2, u^-2*a*u^2*a*u^-2, u^-4*a^2*u^2 ]
Enter AssignGlobals(LoadRCWAExamples().CollatzlikePerms); in order to assign the global variables defined in this section.
In this section, we would like to show that the group \(G\) generated by the two permutations \(n \mapsto n + 1\) and \(\tau_{1(2),0(4)}\) acts 3-transitively, but not 4-transitively on the set of integers.
gap> G := Group(ClassShift(0,1),ClassTransposition(1,2,0,4)); <rcwa group over Z with 2 generators> gap> IsTame(G); false gap> (G.1^-2*G.2)^3*(G.1^2*G.2)^3; # G <> the free product C_infty * C_2. IdentityMapping( Integers ) gap> Display(G:CycleNotation:=false); Wild rcwa group over Z, generated by [ Tame rcwa permutation of Z: n -> n + 1 Rcwa permutation of Z with modulus 4, of order 2 / | 2n-2 if n in 1(2) n |-> < (n+2)/2 if n in 0(4) | n if n in 2(4) \ ]
This group acts transitively on ℤ, since already the cyclic group generated by the first of the two generators does so. Next we have to show that it acts 2-transitively. We essentially proceed as in the example in the previous section, by checking that the stabilizer of 0 acts transitively on \(ℤ \setminus \{0\}\).
gap> gens := [ClassShift(0,1)^-1,ClassTransposition(1,2,0,4), > ClassShift(0,1)];; gap> tups := Concatenation(List([1..6],k->Tuples([-1,0,1],k)));; gap> tups := Filtered(tups,tup->ForAll([[0,0],[-1,1],[1,-1]], > l->PositionSublist(tup,l)=fail));; gap> Length(tups); 189 gap> stab := [];; gap> for tup in tups do > n := 0; > for i in tup do n := n^gens[i+2]; od; > if n = 0 then Add(stab,tup); fi; > od; gap> stabelm := List(stab,tup->Product(List(tup,i->gens[i+2])));; gap> Collected(List(stabelm,Modulus)); [ [ 4, 6 ], [ 8, 4 ], [ 16, 3 ] ] gap> decs := List(stabelm,DecreasingOn); [ 0(4), 3(4), 0(4), 3(4), 2(4), 0(4), 4(8), 2(4), 2(4), 0(4), 1(4), 0(8), 3(8) ] gap> Union(decs); Integers
Similar as in the previous section, it remains to check that the integers with small
absolute value all lie in the orbit containing 1 under the action of the stabilizer of 0:
gap> Maximum(List(stabelm,f->Maximum(List(Coefficients(f), > c->AbsInt(c[2]))))); 21 gap> S := [1];; gap> for elm in stabelm do S := Union(S,S^elm,S^(elm^-1)); od; gap> IsSubset(S,Difference([-21..21],[0])); # Not yet .. false gap> for elm in stabelm do S := Union(S,S^elm,S^(elm^-1)); od; gap> IsSubset(S,Difference([-21..21],[0])); # ... but now! true
Now we have to check for 3-transitivity. Since we cannot find for every residue class an element of the pointwise stabilizer of \(\{0,1\}\) which properly divides its elements, we also have to take additions and subtractions into consideration. Since the moduli of all of our stabilizer elements are quite small, simply looking at sets of representatives is cheap:
gap> tups := Concatenation(List([1..10],k->Tuples([-1,0,1],k)));; gap> tups := Filtered(tups,tup->ForAll([[0,0],[-1,1],[1,-1]], > l->PositionSublist(tup,l)=fail));; gap> Length(tups); 3069 gap> stab := [];; gap> for tup in tups do > l := [0,1]; > for i in tup do l := List(l,n->n^gens[i+2]); od; > if l = [0,1] then Add(stab,tup); fi; > od; gap> Length(stab); 10 gap> stabelm := List(stab,tup->Product(List(tup,i->gens[i+2])));; gap> Maximum(List(stabelm,Modulus)); 8 gap> Maximum(List(stabelm, > f->Maximum(List(Coefficients(f),c->AbsInt(c[2]))))); 8 gap> decsp := List(stabelm,elm->Filtered([9..16],n->n^elm<n)); [ [ 9, 13 ], [ 10, 12, 14, 16 ], [ 12, 16 ], [ 9, 13 ], [ 12, 16 ], [ 9, 11, 13, 15 ], [ 9, 11, 13, 15 ], [ 12, 16 ], [ 12, 16 ], [ 9, 11, 13, 15 ] ] gap> Union(decsp); [ 9 .. 16 ] gap> decsm := List(stabelm,elm->Filtered([-16..-9],n->n^elm>n)); [ [ -15, -13, -11, -9 ], [ -16, -12 ], [ -16, -12 ], [ -15, -11 ], [ -16, -14, -12, -10 ], [ -15, -11 ], [ -15, -11 ], [ -16, -14, -12, -10 ], [ -16, -14, -12, -10 ], [ -15, -11 ] ] gap> Union(decsm); [ -16 .. -9 ] gap> S := [2];; gap> for elm in stabelm do S := Union(S,S^elm,S^(elm^-1)); od; gap> IsSubset(S,Difference([-8..8],[0,1])); true
At this point we have established 3-transitivity. It remains to check that the group \(G\) does not act 4-transitively. We do this by checking that it is not transitive on 4-tuples (mod 4). Since \(n\) mod 8 determines the image of \(n\) under a generator of \(G\) (mod 4), it suffices to compute (mod 8):
gap> orb := [[0,1,2,3]];; gap> extend := function () > local gen; > for gen in gens do > orb := Union(orb,List(orb,l->List(l,n->n^gen) mod 8)); > od; > end;; gap> repeat > old := ShallowCopy(orb); > extend(); Print(Length(orb),"\n"); > until orb = old; 7 27 97 279 573 916 1185 1313 1341 1344 1344 gap> Length(Set(List(orb,l->l mod 4))); 120 gap> last < 4^4; true
This shows that \(G\) acts not 4-transitively on ℤ. The corresponding calculation for 3-tuples looks as follows:
gap> orb := [[0,1,2]];; gap> repeat > old := ShallowCopy(orb); > extend(); Print(Length(orb),"\n"); > until orb = old; 7 27 84 207 363 459 503 512 512 gap> Length(Set(List(orb,l->l mod 4))); 64 gap> last = 4^3; true
Needless to say that the latter kind of argumentation is not suitable for proving, but only for disproving \(k\)-transitivity.
The iterates of an integer under the Collatz mapping \(T\) seem to approach its contraction centre -- this is the finite set where all trajectories end up after a finite number of steps -- rather quickly and do not get very large before doing so (of course this is a purely heuristic statement as the \(3n+1\) conjecture has not been proved so far!):
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; gap> S0 := LikelyContractionCentre(T,100,1000); #I Warning: `LikelyContractionCentre' is highly probabilistic. The returned result can only be regarded as a rough guess. See ?LikelyContractionCentre for more information. [ -136, -91, -82, -68, -61, -55, -41, -37, -34, -25, -17, -10, -7, -5, -1, 0, 1, 2 ] gap> S0^T = S0; # This holds by definition of the contraction centre. true gap> List([1..30],n->Length(Trajectory(T,n,S0))); [ 1, 1, 5, 2, 4, 6, 11, 3, 13, 5, 10, 7, 7, 12, 12, 4, 9, 14, 14, 6, 6, 11, 11, 8, 16, 8, 70, 13, 13, 13 ] gap> Maximum(List([1..1000],n->Length(Trajectory(T,n,S0)))); 113 gap> Maximum(List([1..1000],n->Maximum(Trajectory(T,n,S0)))); 125252
The following mapping seems to be contracting as well, but its trajectories are much longer:
gap> f6 := RcwaMapping([[ 1,0,6],[ 5, 1,6],[ 7,-2,6], > [11,3,6],[11,-2,6],[11,-1,6]]);; gap> Display(f6); Rcwa mapping of Z with modulus 6 / | n/6 if n in 0(6) | (5n+1)/6 if n in 1(6) | (7n-2)/6 if n in 2(6) n |-> < (11n+3)/6 if n in 3(6) | (11n-2)/6 if n in 4(6) | (11n-1)/6 if n in 5(6) | \ gap> S0 := LikelyContractionCentre(f6,1000,100000);; #I Warning: `LikelyContractionCentre' is highly probabilistic. The returned result can only be regarded as a rough guess. See ?LikelyContractionCentre for more information. gap> Trajectory(f6,25,S0); [ 25, 21, 39, 72, 12, 2 ] gap> List([1..100],n->Length(Trajectory(f6,n,S0))); [ 1, 1, 3, 4, 1, 2, 3, 2, 1, 5, 7, 2, 8, 17, 3, 16, 1, 4, 17, 6, 5, 2, 5, 5, 6, 1, 4, 2, 15, 1, 1, 3, 2, 5, 13, 3, 2, 3, 4, 1, 8, 4, 4, 2, 7, 19, 23517, 3, 9, 3, 1, 18, 14, 2, 20, 23512, 14, 2, 6, 6, 1, 4, 19, 12, 23511, 8, 23513, 10, 1, 13, 13, 3, 1, 23517, 7, 20, 7, 9, 9, 6, 12, 8, 6, 18, 14, 23516, 31, 12, 23545, 4, 21, 19, 5, 1, 17, 17, 13, 19, 6, 23515 ] gap> Maximum(Trajectory(f6,47,S0)); 7363391777762473304431877054771075818733690108051469808715809256737742295\ 45698886054
Computing the trajectory of 3224 takes quite a while -- this trajectory ascends to about \(3 \cdot 10^{2197}\), before it approaches the fixed point 2 after 19949562 steps.
When constructing the mapping f6, the denominators of the partial mappings have been chosen to be equal and the numerators have been chosen to be numbers coprime to the common denominator, whose product is just a little bit smaller than the Modulus(f6)th power of the denominator. In the example we have \(5 \cdot 7 \cdot 11^3 = 46585\) and \(6^6 = 46656\).
Although the trajectories of T are much shorter than those of f6, it seems likely that this does not make the problem of deciding whether the mapping T is contracting essentially easier -- even for mappings with much shorter trajectories than T the problem seems to be equally hard. A solution can usually only be found in trivial cases, i.e. for example when there is some \(k\) such that applying the \(k\)th power of the respective mapping to any integer decreases its absolute value.
Enter AssignGlobals(LoadRCWAExamples().SlowlyContractingMappings); in order to assign the global variables defined in this section.
In [And00], P. Andaloro has shown that proving that trajectories of integers \(n \in 1(16)\) under the Collatz mapping always contain 1 would be sufficient to prove the \(3n+1\) conjecture. In the sequel, this result is verified by RCWA. Checking that the union of the images of the residue class 1(16) under powers of the Collatz mapping \(T\) contains \(ℤ \setminus 0(3)\) is obviously enough. Thus we put \(S := 1(16)\), and successively unite the set \(S\) with its image under \(T\):
gap> T := RcwaMapping([[1,0,2],[3,1,2]]); <rcwa mapping of Z with modulus 2> gap> S := ResidueClass(Integers,16,1); 1(16) gap> S := Union(S,S^T); 1(16) U 2(24) gap> S := Union(S,S^T); 1(12) U 2(24) U 17(48) U 33(48) gap> S := Union(S,S^T); <union of 30 residue classes (mod 144)> gap> S := Union(S,S^T); <union of 42 residue classes (mod 144)> gap> S := Union(S,S^T); <union of 172 residue classes (mod 432)> gap> S := Union(S,S^T); <union of 676 residue classes (mod 1296)> gap> S := Union(S,S^T); <union of 810 residue classes (mod 1296)> gap> S := Union(S,S^T); <union of 2638 residue classes (mod 3888)> gap> S := Union(S,S^T); <union of 33 residue classes (mod 48)> gap> S := Union(S,S^T); <union of 33 residue classes (mod 48)> gap> Union(S,ResidueClass(Integers,3,0)); # Et voila ... Integers
Further similar computations are shown in Section 7.17.
Enter AssignGlobals(LoadRCWAExamples().CollatzMapping); in order to assign the global variables defined in this section.
In [ML87], K. R. Matthews and G. M. Leigh have shown that two trajectories of the following (surjective, but not injective) mappings are acyclic (mod \(x\)) and divergent:
gap> x := Indeterminate(GF(4),1);; SetName(x,"x"); gap> R := PolynomialRing(GF(2),1); GF(2)[x] gap> ML1 := RcwaMapping(R,x,[[1,0,x],[(x+1)^3,1,x]]*One(R));; gap> ML2 := RcwaMapping(R,x,[[1,0,x],[(x+1)^2,1,x]]*One(R));; gap> Display(ML1); Rcwa mapping of GF(2)[x] with modulus x / | P/x if P in 0(x) P |-> < ((x^3+x^2+x+1)*P + 1)/x if P in 1(x) | \ gap> Display(ML2); Rcwa mapping of GF(2)[x] with modulus x / | P/x if P in 0(x) P |-> < ((x^2+1)*P + 1)/x if P in 1(x) | \ gap> List([ML1,ML2],IsSurjective); [ true, true ] gap> List([ML1,ML2],IsInjective); [ false, false ] gap> traj1 := Trajectory(ML1,One(R),16); [ 1, x^2+x+1, x^4+x^2+x, x^3+x+1, x^5+x^4+x^2, x^4+x^3+x, x^3+x^2+1, x^5+x^2+1, x^7+x^6+x^5+x^3+1, x^9+x^7+x^6+x^5+x^3+x+1, x^11+x^10+x^8+x^7+x^6+x^5+x^2, x^10+x^9+x^7+x^6+x^5+x^4+x, x^9+x^8+x^6+x^5+x^4+x^3+1, x^11+x^8+x^7+x^6+x^4+x+1, x^13+x^12+x^11+x^8+x^7+x^6+x^4, x^12+x^11+x^10+x^7+x^6+x^5+x^3 ] gap> traj2 := Trajectory(ML2,(x^3+x+1)*One(R),16); [ x^3+x+1, x^4+x+1, x^5+x^3+x^2+x+1, x^6+x^3+1, x^7+x^5+x^4+x^2+x, x^6+x^4+x^3+x+1, x^7+x^4+x^3+x+1, x^8+x^6+x^5+x^4+x^3+x+1, x^9+x^6+x^3+x+1, x^10+x^8+x^7+x^5+x^4+x+1, x^11+x^8+x^7+x^5+x^4+x^3+x^2+x+1, x^12+x^10+x^9+x^8+x^7+x^5+1, x^13+x^10+x^7+x^4+x, x^12+x^9+x^6+x^3+1, x^13+x^11+x^10+x^8+x^7+x^5+x^4+x^2+x, x^12+x^10+x^9+x^7+x^6+x^4+x^3+x+1 ]
The pattern which Matthews and Leigh used to show the divergence of the above trajectories can be recognized easily by looking at the corresponding Markov chains with the two states 0 mod \(x\) and 1 mod \(x\):
gap> traj1modx := Trajectory(ML1,One(R),400,x);; gap> traj2modx := Trajectory(ML2,(x^3+x+1)*One(R),600,x);; gap> List(traj1modx{[1..150]},val->Position([Zero(R),One(R)],val)-1); [ 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ] gap> List(traj2modx{[1..150]},val->Position([Zero(R),One(R)],val)-1); [ 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 ]
What is important here are the lengths of the intervals between two changes from one state to the other:
gap> ChangePoints := l->Filtered([1..Length(l)-1],pos->l[pos]<>l[pos+1]);; gap> Diffs := l->List([1..Length(l)-1],pos->l[pos+1]-l[pos]);; gap> Diffs(ChangePoints(traj1modx)); # The pattern in the first ... [ 1, 1, 2, 4, 2, 2, 4, 8, 4, 4, 8, 16, 8, 8, 16, 32, 16, 16, 32, 64, 32, 32, 64 ] gap> Diffs(ChangePoints(traj2modx)); # ... and in the second example. [ 1, 7, 1, 1, 1, 13, 1, 1, 1, 1, 1, 1, 1, 25, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 49, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 97, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 193, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ] gap> Diffs(ChangePoints(last)); # Make this a bit more obvious. [ 1, 3, 1, 7, 1, 15, 1, 31, 1, 63, 1 ]
This looks clearly acyclic, thus the trajectories diverge. Needless to say however that this computational evidence does not replace the proof along these lines given in the article cited above, but just sheds a light on the idea behind it.
Enter AssignGlobals(LoadRCWAExamples().MatthewsLeigh); in order to assign the global variables defined in this section.
We enter some wild rcwa permutation:
gap> u := RcwaMapping([[3,0,5],[9,1,5],[3,-1,5],[9,-2,5],[9,4,5]]);; gap> IsTame(u);; gap> Display(u); Wild rcwa permutation of Z with modulus 5 / | 3n/5 if n in 0(5) | (9n+1)/5 if n in 1(5) n |-> < (3n-1)/5 if n in 2(5) | (9n-2)/5 if n in 3(5) | (9n+4)/5 if n in 4(5) \
We would like to compute the order of \([u,n \mapsto n + k]\) and \([u^2,n \mapsto n + k]\) for different values of \(k\):
gap> nu := ClassShift(0,1);; # n -> n + 1 gap> l := Filtered([0..100],k->IsTame(Comm(u,nu^k))); [ 0, 2, 3, 5, 6, 9, 10, 12, 13, 15, 17, 18, 20, 21, 24, 25, 27, 28, 30, 32, 33, 35, 36, 39, 40, 42, 43, 45, 47, 48, 50, 51, 54, 55, 57, 58, 60, 62, 63, 65, 66, 69, 70, 72, 73, 75, 77, 78, 80, 81, 84, 85, 87, 88, 90, 92, 93, 95, 96, 99, 100 ] gap> List(l,k->Order(Comm(u,nu^k))); [ 1, 6, 5, 3, 5, 5, 3, infinity, 7, infinity, 7, 5, 3, infinity, infinity, 3, 5, 7, infinity, 7, infinity, 3, 5, 5, 3, 5, infinity, infinity, infinity, 5, 3, 5, 5, 3, infinity, 7, infinity, 7, 5, 3, infinity, infinity, 3, 5, 7, infinity, 7, infinity, 3, 5, 5, 3, 5, infinity, infinity, infinity, 5, 3, 5, 5, 3 ] gap> u2 := u^2; <wild rcwa permutation of Z with modulus 25> gap> Filtered([1..16],k->IsTame(Comm(u2,nu^k))); # k<15->[u^2,nu^k] wild! [ 15 ] gap> Order(Comm(u2,nu^15)); infinity gap> u2nu17 := Comm(u2,nu^17); <rcwa permutation of Z with modulus 81> gap> cycs := ShortCycles(u2nu17,[-100..100],100);; gap> List(cycs,Length); [ 72, 73, 72, 72, 72, 73, 72, 72, 73, 72, 72, 73, 72, 72, 73, 72, 72, 73, 72, 72, 73, 72, 72 ] gap> Lcm(last); 5256 gap> u2nu17^5256; # This element has indeed order 2^3*3^2*73 = 5256. IdentityMapping( Integers ) gap> u2nu18 := Comm(u2,nu^18); <rcwa permutation of Z with modulus 81> gap> cycs := ShortCycles(u2nu18,[-100..100],100);; gap> List(cycs,Length); [ 21, 22, 22, 22, 21, 22, 22, 21, 22, 22, 21, 22, 21, 22, 22, 21, 22, 22, 21, 22, 22, 21, 22 ] gap> Lcm(last); 462 gap> u2nu18^462; # This is an element of order 2*3*7*11 = 462. IdentityMapping( Integers ) gap> List([Comm(u2,nu^20),Comm(u2,nu^25),Comm(u2,nu^30)],Order); [ 29, 9, 15 ]
We observe that our commutators have various different orders, and that the prime factors of these orders are not all very small
.
Enter AssignGlobals(LoadRCWAExamples().CollatzlikePerms); in order to assign the global variables defined in this section.
In this section, we have a look at the following subgroup of CT(GF(2)[x]):
gap> x := Indeterminate(GF(2));; SetName(x,"x"); gap> R := PolynomialRing(GF(2),1); GF(2)[x] gap> a := ClassTransposition(0,x,1,x);; gap> b := ClassTransposition(0,x^2+1,1,x^2+1);; gap> c := ClassTransposition(1,x,0,x^2+x);; gap> G := Group(a,b,c); <rcwa group over GF(2)[x] with 3 generators> gap> Display(G); Rcwa group over GF(2)[x], generated by [ Rcwa permutation of GF(2)[x]: P -> P + Z(2)^0 Rcwa permutation of GF(2)[x] with modulus x^2+1, of order 2 / | P + 1 if P in 0(x^2+1) U 1(x^2+1) P |-> < P if P in x(x^2+1) U x+1(x^2+1) | \ Rcwa permutation of GF(2)[x] with modulus x^2+x, of order 2 / | (x+1)*P + x+1 if P in 1(x) P |-> < (P + x+1)/(x+1) if P in 0(x^2+x) | P if P in x(x^2+x) \ ]
We can easily find 2 normal subgroups of G:
gap> N1 := Subgroup(G,[a*b,a*c]); <rcwa group over GF(2)[x] with 2 generators> gap> IsNormal(G,N1); true gap> Index(G,N1); 2 gap> G/N1; Group([ (1,2), (1,2), (1,2) ]) gap> N2 := Subgroup(G,[a*b*c,a*c]);; gap> IsNormal(G,N2); true gap> IsSubgroup(N1,N2); false
Products of even numbers of generators of G may have infinite order. For example, we have
gap> Order(a*b); 2 gap> Order(a*c); infinity gap> Order(b*c); infinity
We would like to have a look at orders of products of odd numbers of generators. In order to restrict our considerations to essentially different
products (as far as we can easily do this), we use the following auxiliary function:
NormedWords := function ( F, lng )
local words, gens, tuples, w;
gens := GeneratorsOfGroup(F);
tuples := EnumeratorOfTuples([1..3],lng);
words := [];
for w in tuples do
if (w[1] = 1 or not 1 in w)
and PositionSublist(w,[1,1]) = fail
and PositionSublist(w,[2,2]) = fail
and PositionSublist(w,[3,3]) = fail
and PositionSublist(w,[2,1]) = fail
and w[1] < w[lng]
and w{[1,lng]} <> [1,2]
and (w{[1..3]} = [1,2,3] or PositionSublist(w,[1,2,3]) = fail)
then Add(words,w); fi;
od;
words := List(words,word->Product(List(word,i->gens[i])));
return words;
end;
Now let's compute the possible orders of products of 3, 5, 7 or 9 generators:
gap> F := FreeGroup("a","b","c");; gap> phi := EpimorphismByGenerators(F,G); [ a, b, c ] -> [ ClassTransposition(0,x,1,x), ClassTransposition(0,x^2+1,1,x^2+1), ClassTransposition(1,x,0,x^2+x) ] gap> B3 := NormedWords(F,3); [ a*b*c ] gap> B3 := List(B3,g->g^phi); [ <rcwa permutation of GF(2)[x] with modulus x^3+x> ] gap> List(B3,Order); [ 20 ] gap> B5 := NormedWords(F,5); [ a*b*c*a*c, a*b*c*b*c ] gap> B5 := List(B5,g->g^phi); [ <rcwa permutation of GF(2)[x] with modulus x^3+x>, <rcwa permutation of GF(2)[x] with modulus x^4+x^3+x^2+x> ] gap> List(B5,Order); [ 12, 12 ] gap> B7 := NormedWords(F,7); [ a*b*c*a*c*a*c, a*b*c*a*c*b*c, a*b*c*b*c*a*c, a*b*c*b*c*b*c ] gap> B7 := List(B7,g->g^phi); [ <rcwa permutation of GF(2)[x] with modulus x^4+x^3+x^2+x>, <rcwa permutation of GF(2)[x] with modulus x^5+x>, <rcwa permutation of GF(2)[x] with modulus x^4+x^3+x^2+x>, <rcwa permutation of GF(2)[x] with modulus x^5+x> ] gap> List(B7,Order); [ 12, 12, 12, 30 ] gap> B9 := NormedWords(F,9); [ a*b*c*a*b*c*a*b*c, a*b*c*a*c*a*c*a*c, a*b*c*a*c*a*c*b*c, a*b*c*a*c*b*c*a*c, a*b*c*a*c*b*c*b*c, a*b*c*b*c*a*c*a*c, a*b*c*b*c*a*c*b*c, a*b*c*b*c*b*c*a*c, a*b*c*b*c*b*c*b*c ] gap> B9 := List(B9,g->g^phi);; gap> List(B9,Order); [ 20, 4, 30, 12, 42, 30, 4, 42, 12 ]
Enter AssignGlobals(LoadRCWAExamples().OddNumberOfGens_FiniteOrder); in order to assign the global variables defined in this section.
We enter a 2-generated abelian wild rcwa group over GF(4)[\(x\)]:
gap> x := Indeterminate(GF(4),1);; SetName(x,"x"); gap> R := PolynomialRing(GF(4),1); GF(2^2)[x] gap> e := One(GF(4));; gap> p := x^2 + x + e;; q := x^2 + e;; gap> r := x^2 + x + Z(4);; s := x^2 + x + Z(4)^2;; gap> cg := List( AllResidues(R,x^2), pol -> [ p, p * pol mod q, q ] );; gap> ch := List( AllResidues(R,x^2), pol -> [ r, r * pol mod s, s ] );; gap> g := RcwaMapping( R, q, cg ); <rcwa mapping of GF(2^2)[x] with modulus x^2+1> gap> h := RcwaMapping( R, s, ch ); <rcwa mapping of GF(2^2)[x] with modulus x^2+x+Z(2^2)^2> gap> List([g,h],IsTame); [ false, false ] gap> G := Group(g,h); <rcwa group over GF(2^2)[x] with 2 generators> gap> IsAbelian(G); true gap> IsTame(G); false
It is easy to see that all orbits on GF(4)[\(x\)] under the action of G are finite.
Now we compute the action of the group G on one of its orbits, and make some statistics of the orbits of G containing polynomials of degree less than 4:
gap> orb := Orbit(G,x^5); [ x^5, x^5+x^4+x^2+1, x^5+x^3+x^2+Z(2^2)*x+Z(2)^0, x^5+x^3, x^5+x^4+x^3+x^2+Z(2^2)^2*x+Z(2^2)^2, x^5+x, x^5+x^4+x^3, x^5+x^2+Z(2^2)^2*x, x^5+x^4+x^2+x, x^5+x^3+x^2+Z(2^2)^2*x+Z(2)^0, x^5+x^4+Z(2^2)*x+Z(2^2), x^5+x^3+x, x^5+x^4+x^3+x^2+Z(2^2)*x+Z(2^2), x^5+x^4+x^3+x+1, x^5+x^2+Z(2^2)*x, x^5+x^4+Z(2^2)^2*x+Z(2^2)^2 ] gap> H := Action(G,orb); Group([ (1,2,4,7,6,9,12,14)(3,5,8,11,10,13,15,16), (1,3,6,10)(2,5,9,13)(4,8,12,15)(7,11,14,16) ]) gap> IsAbelian(H); # check ... true gap> IsCyclic(H); # H, and therefore also G, is not cyclic false gap> Exponent(H); 8 gap> Collected(List(ShortOrbits(G,AllResidues(R,x^4),100),Length)); [ [ 1, 4 ], [ 2, 6 ], [ 4, 12 ], [ 8, 24 ] ]
Changing the generators a little changes the structure of the group and its action on the underlying ring a lot:
gap> cg[1][2] := cg[1][2] + (x^2 + e) * p * q;; gap> ch[7][2] := ch[7][2] + x * r * s;; gap> g := RcwaMapping( R, q, cg );; h := RcwaMapping( R, s, ch );; gap> G := Group(g,h); <rcwa group over GF(2^2)[x] with 2 generators> gap> IsAbelian(G); false gap> Support(G); GF(2^2)[x] \ [ 1, Z(2^2), Z(2^2)^2 ] gap> orb := Orbit(G,Zero(R));; gap> Length(orb); 87 gap> StructureDescription(Action(G,orb)); "A87" gap> Collected(List(orb,DegreeOfLaurentPolynomial)); [ [ -infinity, 1 ], [ 1, 2 ], [ 2, 4 ], [ 3, 16 ], [ 4, 64 ] ] gap> S := AllResidues(R,x^6);; gap> orbs := ShortOrbits(G,S,-1:finite);; gap> List(orbs,Length); [ 87, 1, 1, 1, 2, 2, 2, 2, 2, 4, 4, 4, 20, 4, 12, 4, 20, 4, 4, 12, 8, 8, 48, 48, 16, 8, 8, 56, 8, 88, 8, 8, 8, 400, 16, 48, 16, 16, 16, 80, 16, 16, 16, 96, 32, 192, 32, 16, 16, 416, 16, 48, 16, 16, 880, 16, 16, 16, 16, 16, 16, 16, 16, 16, 848, 16, 16, 32, 16, 16, 16, 16, 16, 16, 16 ] gap> Position(last,880); 55 gap> Set(orbs[55],DegreeOfLaurentPolynomial); # all elm's have same degree [ 5 ] gap> H := Action(G,orbs[55]);; gap> IsPrimitive(H,MovedPoints(H)); false gap> List(Blocks(H,MovedPoints(H)),Length); [ 110, 110, 110, 110, 110, 110, 110, 110 ]
Enter AssignGlobals(LoadRCWAExamples().AbelianGroupOverPolynomialRing); in order to assign the global variables defined in this section.
Presently there is no general method available for testing wild rcwa groups for solvability. However, sometimes the question for solvability can be answered anyway. In the example below, the idea is to find a subgroup U which acts on a finite set S of integers, and which induces on S a non-solvable finite permutation group:
gap> a := RcwaMapping([[3,0,2],[3, 1,4],[3,0,2],[3,-1,4]]);; gap> b := RcwaMapping([[3,0,2],[3,13,4],[3,0,2],[3,-1,4]]);; gap> G := Group(a,b);; gap> ShortOrbits(Group(Comm(a,b)),[-10..10],100); [ [ -10 ], [ -9 ], [ -30, -21, -14, -13, -11, -8 ], [ -7 ], [ -6 ], [ -12, -5, -4, -3, -2, 1 ], [ -1 ], [ 0 ], [ 2 ], [ 3 ], [ 4, 5, 6, 7, 10, 15 ], [ 8 ], [ 9 ] ] gap> S := [ 4, 5, 6, 7, 10, 15 ];; gap> Cycle(Comm(a,b),4); [ 4, 7, 10, 15, 5, 6 ] gap> elm := RepresentativeAction(G,S,Permuted(S,(1,4)),OnTuples); <rcwa permutation of Z with modulus 81> gap> List(S,n->n^elm); [ 7, 5, 6, 4, 10, 15 ] gap> U := Group(Comm(a,b),elm); <rcwa group over Z with 2 generators> gap> Action(U,S); Group([ (1,4,5,6,2,3), (1,4) ]) gap> IsNaturalSymmetricGroup(last); true
Thus the subgroup U induces on S a natural symmetric group of degree 6. Therefore the group G is not solvable. We conclude this example by factoring the group element elm into generators:
gap> F := FreeGroup("a","b"); <free group on the generators [ a, b ]> gap> RepresentativeActionPreImage(G,S,Permuted(S,(1,4)),OnTuples,F); a^-2*b^-2*a*b*a^-1*b*a*b^-2*a gap> a^-2*b^-2*a*b*a^-1*b*a*b^-2*a = elm; true
Enter AssignGlobals(LoadRCWAExamples().CheckingForSolvability); in order to assign the global variables defined in this section.
We start with something one can observe when trying to transfer
an rcwa mapping from the ring of integers to one of its localizations:
gap> a := RcwaMapping([[3,0,2],[3,1,4],[3,0,2],[3,-1,4]]);; gap> IsBijective(a); true gap> a2 := LocalizedRcwaMapping(a,2); <rcwa mapping of Z_( 2 ) with modulus 4> gap> IsSurjective(a2); # As expected true gap> IsInjective(a2); # Why not?? false gap> 0^a2; 0 gap> (1/3)^a2; # That's the reason! 0
The above can also be explained easily by pointing out that the modulus of the inverse of a is 3, and that 3 is a unit of \(ℤ_{(2)}\). Moving to \(ℤ_{(2,3)}\) solves this problem:
gap> a23 := SemilocalizedRcwaMapping(a,[2,3]); <rcwa mapping of Z_( 2, 3 ) with modulus 4> gap> IsBijective(a23); true
We get additional finite cycles, e.g.:
gap> List(ShortOrbits(Group(a23),[0..50]/5,50),orb->Cycle(a23,orb[1])); [ [ 0 ], [ 1/5, 2/5, 3/5 ], [ 4/5, 6/5, 9/5, 8/5, 12/5, 18/5, 27/5, 19/5, 13/5, 11/5, 7/5 ], [ 1 ], [ 2, 3 ], [ 14/5, 21/5, 17/5 ], [ 16/5, 24/5, 36/5, 54/5, 81/5, 62/5, 93/5, 71/5, 52/5, 78/5, 117/5, 89/5, 68/5, 102/5, 153/5, 116/5, 174/5, 261/5, 197/5, 149/5, 113/5, 86/5, 129/5, 98/5, 147/5, 109/5, 83/5, 61/5, 47/5, 34/5, 51/5, 37/5, 29/5, 23/5 ], [ 4, 6, 9, 7, 5 ] ] gap> List(last,Length); [ 1, 3, 11, 1, 2, 3, 34, 5 ] gap> List(ShortOrbits(Group(a23),[0..50]/7,50),orb->Cycle(a23,orb[1])); [ [ 0 ], [ -1/7, 1/7 ], [ 2/7, 3/7, 4/7, 6/7, 9/7, 5/7 ], [ 1 ], [ 2, 3 ], [ 4, 6, 9, 7, 5 ] ] gap> List(last,Length); [ 1, 2, 6, 1, 2, 5 ]
However the structure of a group with prime set \(\mathbb{P}\) remains invariant under the transfer
from ℤ to \(ℤ_{(\mathbb{P})}\).
Transferring
a non-invertible rcwa mapping from the ring of integers to some of its (semi)localizations can also turn it into an invertible one:
gap> v := RcwaMapping([[6,0,1],[1,-7,2],[6,0,1],[1,-1,1], > [6,0,1],[1, 1,2],[6,0,1],[1,-1,1]]);; gap> Display(v); Rcwa mapping of Z with modulus 8 / | 6n if n in 0(2) | n-1 if n in 3(4) n |-> < (n-7)/2 if n in 1(8) | (n+1)/2 if n in 5(8) | \ gap> IsInjective(v); true gap> IsSurjective(v); false gap> Image(v); Z \ 4(12) U 8(12) gap> Difference(Integers,last); 4(12) U 8(12) gap> v2 := LocalizedRcwaMapping(v,2); <rcwa mapping of Z_( 2 ) with modulus 8> gap> IsBijective(v2); true gap> Display(v2^-1); Rcwa permutation of Z_( 2 ) with modulus 4 / | 1/3 n / 2 if n in 0(4) | 2 n + 7 if n in 1(4) n |-> < n + 1 if n in 2(4) | 2 n - 1 if n in 3(4) | \ gap> S := ResidueClass(Z_pi(2),2,0);; l := [S];; gap> for i in [1..10] do Add(l,l[Length(l)]^v2); od; gap> l; # Visibly v2 is wild ... [ 0(2), 0(4), 0(8), 0(16), 0(32), 0(64), 0(128), 0(256), 0(512), 0(1024), 0(2048) ] gap> w2 := RcwaMapping(Z_pi(2),[[1,0,2],[2,-1,1],[1,1,1],[2,-1,1]]);; gap> v2w2 := Comm(v2,w2);; v2w2^-1;; gap> Display(v2w2); Rcwa permutation of Z_( 2 ) with modulus 8 / | 3 n if n in 2(4) | n + 4 if n in 1(8) n |-> < n - 4 if n in 5(8) | n if n in 0(4) U 3(4) | \
Again, viewed as an rcwa mapping of the integers the commutator given at the end of the example would not be surjective.
Enter AssignGlobals(LoadRCWAExamples().Semilocals); in order to assign the global variables defined in this section.
We define an rcwa mapping x of order 257 with modulus 32. The easiest way to construct such a mapping is to prescribe a transition graph and then to assign suitable affine mappings to its vertices.
gap> x_257 := RcwaMapping( > [[ 16, 2, 1], [ 16, 18, 1], [ 1, 16, 1], [ 16, 18, 1], > [ 1, 16, 1], [ 16, 18, 1], [ 1, 16, 1], [ 16, 18, 1], > [ 1, 16, 1], [ 16, 18, 1], [ 1, 16, 1], [ 16, 18, 1], > [ 1, 16, 1], [ 16, 18, 1], [ 1, 16, 1], [ 16, 18, 1], > [ 1, 0, 16], [ 16, 18, 1], [ 1,-14, 1], [ 16, 18, 1], > [ 1,-14, 1], [ 16, 18, 1], [ 1,-14, 1], [ 16, 18, 1], > [ 1,-14, 1], [ 16, 18, 1], [ 1,-14, 1], [ 16, 18, 1], > [ 1,-14, 1], [ 16, 18, 1], [ 1,-14, 1], [ 1,-31, 1]]);; gap> Order(x_257);; Display(x_257:CycleNotation:=false); Rcwa permutation of Z with modulus 32, of order 257 / | 16n+18 if n in 1(2) \ 31(32) | n+16 if n in 2(32) U 4(32) U 6(32) U 8(32) U 10(32) U | 12(32) U 14(32) | n-14 if n in 18(32) U 20(32) U 22(32) U 24(32) U 26(32) U n |-> < 28(32) U 30(32) | 16n+2 if n in 0(32) | n/16 if n in 16(32) | n-31 if n in 31(32) | \ gap> Display(x_257); Rcwa permutation of Z with modulus 32, of order 257 ( 0(32), 2(512), 18(512), 4(512), 20(512), 6(512), 22(512), 8(512), 24(512), 10(512), 26(512), 12(512), 28(512), 14(512), 30(512), 16(512), 1(32), 34(512), 50(512), 36(512), 52(512), 38(512), 54(512), 40(512), 56(512), 42(512), 58(512), 44(512), 60(512), 46(512), 62(512), 48(512), 3(32), 66(512), 82(512), 68(512), 84(512), 70(512), 86(512), 72(512), 88(512), 74(512), 90(512), 76(512), 92(512), 78(512), 94(512), 80(512), 5(32), 98(512), 114(512), 100(512), 116(512), 102(512), 118(512), 104(512), 120(512), 106(512), 122(512), 108(512), 124(512), 110(512), 126(512), 112(512), 7(32), 130(512), 146(512), 132(512), 148(512), 134(512), 150(512), 136(512), 152(512), 138(512), 154(512), 140(512), 156(512), 142(512), 158(512), 144(512), 9(32), 162(512), 178(512), 164(512), 180(512), 166(512), 182(512), 168(512), 184(512), 170(512), 186(512), 172(512), 188(512), 174(512), 190(512), 176(512), 11(32), 194(512), 210(512), 196(512), 212(512), 198(512), 214(512), 200(512), 216(512), 202(512), 218(512), 204(512), 220(512), 206(512), 222(512), 208(512), 13(32), 226(512), 242(512), 228(512), 244(512), 230(512), 246(512), 232(512), 248(512), 234(512), 250(512), 236(512), 252(512), 238(512), 254(512), 240(512), 15(32), 258(512), 274(512), 260(512), 276(512), 262(512), 278(512), 264(512), 280(512), 266(512), 282(512), 268(512), 284(512), 270(512), 286(512), 272(512), 17(32), 290(512), 306(512), 292(512), 308(512), 294(512), 310(512), 296(512), 312(512), 298(512), 314(512), 300(512), 316(512), 302(512), 318(512), 304(512), 19(32), 322(512), 338(512), 324(512), 340(512), 326(512), 342(512), 328(512), 344(512), 330(512), 346(512), 332(512), 348(512), 334(512), 350(512), 336(512), 21(32), 354(512), 370(512), 356(512), 372(512), 358(512), 374(512), 360(512), 376(512), 362(512), 378(512), 364(512), 380(512), 366(512), 382(512), 368(512), 23(32), 386(512), 402(512), 388(512), 404(512), 390(512), 406(512), 392(512), 408(512), 394(512), 410(512), 396(512), 412(512), 398(512), 414(512), 400(512), 25(32), 418(512), 434(512), 420(512), 436(512), 422(512), 438(512), 424(512), 440(512), 426(512), 442(512), 428(512), 444(512), 430(512), 446(512), 432(512), 27(32), 450(512), 466(512), 452(512), 468(512), 454(512), 470(512), 456(512), 472(512), 458(512), 474(512), 460(512), 476(512), 462(512), 478(512), 464(512), 29(32), 482(512), 498(512), 484(512), 500(512), 486(512), 502(512), 488(512), 504(512), 490(512), 506(512), 492(512), 508(512), 494(512), 510(512), 496(512), 31(32) ) gap> Length(Cycle(x_257,0)); 257
Enter AssignGlobals(LoadRCWAExamples().LongCyclesOfPrimeLength); in order to assign the global variables defined in this section.
We give some examples of how the series of the moduli of powers of a given rcwa mapping of the integers can look like.
gap> a := RcwaMapping([[3,0,2],[3, 1,4],[3,0,2],[3,-1,4]]);; gap> List([0..4],i->Modulus(a^i)); [ 1, 4, 16, 64, 256 ] gap> e1 := RcwaMapping([[1,4,1],[2,0,1],[1,0,2],[2,0,1]]);; gap> e2 := RcwaMapping([[1,4,1],[2,0,1],[1,0,2],[1,0,1], > [1,4,1],[2,0,1],[1,0,1],[1,0,1]]);; gap> List([e1,e2],Order); [ infinity, infinity ] gap> List([1..20],i->Modulus(e1^i)); [ 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 ] gap> List([1..20],i->Modulus(e2^i)); [ 8, 4, 8, 4, 8, 4, 8, 4, 8, 4, 8, 4, 8, 4, 8, 4, 8, 4, 8, 4 ] gap> Display(e2); Rcwa permutation of Z with modulus 8, of order infinity / | n+4 if n in 0(4) | 2n if n in 1(4) n |-> < n/2 if n in 2(8) | n if n in 3(4) U 6(8) | \ gap> e2^2 = Restriction(RcwaMapping([[1,2,1]]),RcwaMapping([[4,0,1]])); true gap> g:=RcwaMapping([[2,2,1],[1, 4,1],[1,0,2],[2,2,1],[1,-4,1],[1,-2,1]]);; gap> h:=RcwaMapping([[2,2,1],[1,-2,1],[1,0,2],[2,2,1],[1,-1,1],[1, 1,1]]);; gap> List([0..7],i->Modulus(g^i)); [ 1, 6, 12, 12, 12, 12, 6, 1 ] gap> List([1..18],i->Modulus((g^3*h)^i)); [ 12, 6, 12, 12, 12, 6, 12, 6, 12, 12, 12, 6, 12, 6, 12, 12, 12, 6 ] gap> u := RcwaMapping([[3,0,5],[9,1,5],[3,-1,5],[9,-2,5],[9,4,5]]);; gap> List([0..3],i->Modulus(u^i)); [ 1, 5, 25, 125 ] gap> v6 := RcwaMapping([[-1,2,1],[1,-1,1],[1,-1,1]]);; gap> List([0..6],i->Modulus(v6^i)); [ 1, 3, 3, 3, 3, 3, 1 ] gap> w8 := RcwaMapping([[-1,3,1],[1,-1,1],[1,-1,1],[1,-1,1]]);; gap> List([0..8],i->Modulus(w8^i)); [ 1, 4, 4, 4, 4, 4, 4, 4, 1 ] gap> z := RcwaMapping([[2,1,1],[1, 1,1],[2,-1,1],[2, -2,1], > [1,6,2],[1, 1,1],[1,-6,2],[2, 5,1], > [1,6,2],[1, 1,1],[1, 1,1],[2, -5,1], > [1,0,1],[1,-4,1],[1, 0,1],[2,-10,1]]);; gap> IsBijective(z); true gap> List([0..25],i->Modulus(z^i)); [ 1, 16, 32, 64, 64, 128, 128, 128, 128, 128, 128, 256, 256, 256, 256, 256, 256, 512, 512, 512, 512, 512, 512, 1024, 1024, 1024 ]
Enter AssignGlobals(LoadRCWAExamples().ModuliOfPowers); in order to assign the global variables defined in this section.
We have a look at the images of the residue class 1(2) under powers of the Collatz mapping.
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; gap> S0 := ResidueClass(Integers,2,1);; gap> S1 := S0^T; 2(3) gap> S2 := S1^T; 1(3) U 8(9) gap> S3 := S2^T; 2(3) U 4(9) gap> S4 := S3^T; Z \ 0(3) U 5(9) gap> S5 := S4^T; Z \ 0(3) U 7(9) gap> S6 := S5^T; Z \ 0(3) gap> S7 := S6^T; Z \ 0(3)
Thus the image gets stable after applying the mapping \(T\) for the 6th time. Hence \(T^6\) maps the residue class 1(2) surjectively onto the union of the residue classes 1(3) and 2(3), which \(T\) stabilizes setwise. Now we would like to determine the preimages of 1(3) and 2(3) in 1(2) under \(T^6\). The residue class 1(2) has to be the disjoint union of these sets.
gap> U := Intersection(PreImage(T^6,ResidueClass(Integers,3,1)),S0); <union of 11 residue classes (mod 64)> gap> V := Intersection(PreImage(T^6,ResidueClass(Integers,3,2)),S0); <union of 21 residue classes (mod 64)> gap> AsUnionOfFewClasses(U); [ 1(64), 5(64), 7(64), 9(64), 21(64), 23(64), 29(64), 31(64), 49(64), 51(64), 59(64) ] gap> AsUnionOfFewClasses(V); [ 3(32), 11(32), 13(32), 15(32), 25(32), 17(64), 19(64), 27(64), 33(64), 37(64), 39(64), 41(64), 53(64), 55(64), 61(64), 63(64) ] gap> Union(U,V) = S0 and Intersection(U,V) = []; # consistency check true
The images of the residue class 0(3) under powers of \(T\) look as follows:
gap> S0 := ResidueClass(Integers,3,0); 0(3) gap> S1 := S0^T; 0(3) U 5(9) gap> S2 := S1^T; 0(3) U 5(9) U 7(9) U 8(27) gap> S3 := S2^T; <union of 20 residue classes (mod 27) (6 classes)> gap> S4 := S3^T; <union of 73 residue classes (mod 81)> gap> S5 := S4^T; Z \ 10(81) U 37(81) gap> S6 := S5^T; Integers gap> S7 := S6^T; Integers
Thus every integer is the image of a multiple of 3 under \(T^6\). This means that it would be sufficient to prove the \(3n+1\) conjecture for multiples of 3. We can obtain the corresponding result for multiples of 5 as follows:
gap> S := [ResidueClass(Integers,5,0)]; [ 0(5) ] gap> for i in [1..12] do Add(S,S[i]^T); od; gap> for s in S do View(s); Print("\n"); od; 0(5) 0(5) U 8(15) 0(5) U 4(15) U 8(15) 0(5) U 2(15) U 4(15) U 8(15) U 29(45) <union of 73 residue classes (mod 135)> <union of 244 residue classes (mod 405)> <union of 784 residue classes (mod 1215)> <union of 824 residue classes (mod 1215)> <union of 2593 residue classes (mod 3645)> <union of 2647 residue classes (mod 3645)> <union of 2665 residue classes (mod 3645)> <union of 2671 residue classes (mod 3645)> 1(3) U 2(3) U 0(15) gap> Union(S[13],ResidueClass(Integers,3,0)); Integers gap> List(S,Si->Float(Density(Si))); [ 0.2, 0.266667, 0.333333, 0.422222, 0.540741, 0.602469, 0.645267, 0.678189, 0.711385, 0.7262, 0.731139, 0.732785, 0.733333 ]
Enter AssignGlobals(LoadRCWAExamples().CollatzMapping); in order to assign the global variables defined in this section.
The Collatz mapping \(T\) is surjective, but not injective:
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);; gap> Display(T); Rcwa mapping of Z with modulus 2 / | n/2 if n in 0(2) n |-> < (3n+1)/2 if n in 1(2) | \ gap> IsInjective(T); IsSurjective(T); false true gap> PreImages(T,2); [ 1, 4 ]
Often, dealing with rcwa permutations is easier. Indeed the Collatz mapping \(T\) can be extended in natural ways to permutations of \(ℤ^2\). For example, the following permutation acts on the second coordinate just like \(T\):
gap> Sigma_T := RcwaMapping( Integers^2, [[1,0],[0,6]], > [[[[2,0],[0,1]],[0,0],2], > [[[4,0],[0,3]],[2,1],2], > [[[2,0],[0,1]],[0,0],2], > [[[4,0],[0,3]],[2,1],2], > [[[4,0],[0,1]],[0,0],2], > [[[4,0],[0,3]],[2,1],2]] ); <rcwa mapping of Z^2 with modulus (1,0)Z+(0,6)Z> gap> IsBijective(Sigma_T); true gap> Display(Sigma_T); Rcwa permutation of Z^2 with modulus (1,0)Z+(0,6)Z / | (2m+1,(3n+1)/2) if (m,n) in (0,1)+(1,0)Z+(0,2)Z | (m,n/2) if (m,n) in (0,0)+(1,0)Z+(0,6)Z U (m,n) |-> < (0,2)+(1,0)Z+(0,6)Z | (2m,n/2) if (m,n) in (0,4)+(1,0)Z+(0,6)Z | \ gap> Display(Sigma_T^-1); Rcwa permutation of Z^2 with modulus (2,0)Z+(0,3)Z / | (m,2n) if (m,n) in (0,0)+(1,0)Z+(0,3)Z U | (0,1)+(1,0)Z+(0,3)Z (m,n) |-> < (m/2,2n) if (m,n) in (0,2)+(2,0)Z+(0,3)Z | ((m-1)/2,(2n-1)/3) if (m,n) in (1,2)+(2,0)Z+(0,3)Z | \
Now, the \(3n+1\) conjecture is equivalent to the assertion that the line \(n=4\) is a set of representatives for the cycles of Sigma_T on the half plane \(n > 0\).
Let's have a look at a part of a cycle of Sigma_T:
gap> Trajectory(Sigma_T,[0,27],75); [ [ 0, 27 ], [ 1, 41 ], [ 3, 62 ], [ 3, 31 ], [ 7, 47 ], [ 15, 71 ], [ 31, 107 ], [ 63, 161 ], [ 127, 242 ], [ 127, 121 ], [ 255, 182 ], [ 255, 91 ], [ 511, 137 ], [ 1023, 206 ], [ 1023, 103 ], [ 2047, 155 ], [ 4095, 233 ], [ 8191, 350 ], [ 8191, 175 ], [ 16383, 263 ], [ 32767, 395 ], [ 65535, 593 ], [ 131071, 890 ], [ 131071, 445 ], [ 262143, 668 ], [ 262143, 334 ], [ 524286, 167 ], [ 1048573, 251 ], [ 2097147, 377 ], [ 4194295, 566 ], [ 4194295, 283 ], [ 8388591, 425 ], [ 16777183, 638 ], [ 16777183, 319 ], [ 33554367, 479 ], [ 67108735, 719 ], [ 134217471, 1079 ], [ 268434943, 1619 ], [ 536869887, 2429 ], [ 1073739775, 3644 ], [ 1073739775, 1822 ], [ 2147479550, 911 ], [ 4294959101, 1367 ], [ 8589918203, 2051 ], [ 17179836407, 3077 ], [ 34359672815, 4616 ], [ 34359672815, 2308 ], [ 68719345630, 1154 ], [ 68719345630, 577 ], [ 137438691261, 866 ], [ 137438691261, 433 ], [ 274877382523, 650 ], [ 274877382523, 325 ], [ 549754765047, 488 ], [ 549754765047, 244 ], [ 1099509530094, 122 ], [ 1099509530094, 61 ], [ 2199019060189, 92 ], [ 2199019060189, 46 ], [ 4398038120378, 23 ], [ 8796076240757, 35 ], [ 17592152481515, 53 ], [ 35184304963031, 80 ], [ 35184304963031, 40 ], [ 70368609926062, 20 ], [ 70368609926062, 10 ], [ 140737219852124, 5 ], [ 281474439704249, 8 ], [ 281474439704249, 4 ], [ 562948879408498, 2 ], [ 562948879408498, 1 ], [ 1125897758816997, 2 ], [ 1125897758816997, 1 ], [ 2251795517633995, 2 ], [ 2251795517633995, 1 ] ] gap> Trajectory(Sigma_T^-1,[0,27],20); [ [ 0, 27 ], [ 0, 54 ], [ 0, 108 ], [ 0, 216 ], [ 0, 432 ], [ 0, 864 ], [ 0, 1728 ], [ 0, 3456 ], [ 0, 6912 ], [ 0, 13824 ], [ 0, 27648 ], [ 0, 55296 ], [ 0, 110592 ], [ 0, 221184 ], [ 0, 442368 ], [ 0, 884736 ], [ 0, 1769472 ], [ 0, 3538944 ], [ 0, 7077888 ], [ 0, 14155776 ] ]
While it seems easy to make conjectures regarding the behaviour of cycles of Sigma_T, obtaining results on it is apparently hard. We observe however that Sigma_T can be written as a product of two permutations of \(ℤ^2\) whose cycles can be described easily:
gap> a := RcwaMapping(Integers^2,[[1,0],[0,2]],[[[[4,0],[0,1]],[0, 0],2], > [[[4,0],[0,1]],[2,-1],2]]); <rcwa mapping of Z^2 with modulus (1,0)Z+(0,2)Z> gap> b := a^-1*Sigma_T; <rcwa permutation of Z^2 with modulus (2,0)Z+(0,3)Z> gap> Display(a); Rcwa permutation of Z^2 with modulus (1,0)Z+(0,2)Z / | (2m,n/2) if (m,n) in (0,0)+(1,0)Z+(0,2)Z (m,n) |-> < (2m+1,(n-1)/2) if (m,n) in (0,1)+(1,0)Z+(0,2)Z | \ gap> Display(b); Rcwa permutation of Z^2 with modulus (2,0)Z+(0,3)Z / | (m,3n+2) if (m,n) in (1,0)+(2,0)Z+(0,1)Z | (m/2,n) if (m,n) in (0,0)+(2,0)Z+(0,3)Z U (m,n) |-> < (0,1)+(2,0)Z+(0,3)Z | (m,n) if (m,n) in (0,2)+(2,0)Z+(0,3)Z | \
It is easy to see that both a and b have infinite order. The cycles of a have roughly hyperbolic shape and run, so to speak, from \((0,\pm \infty)\) to \((\pm \infty,0)\). A given cycle contains only finitely many points both of whose coordinates are nonzero. The fixed points of a are (0,0) and (-1,-1). We have a look at an example of a cycle of a:
gap> Trajectory(a,[1000,1000],15); [ [ 1000, 1000 ], [ 2000, 500 ], [ 4000, 250 ], [ 8000, 125 ], [ 16001, 62 ], [ 32002, 31 ], [ 64005, 15 ], [ 128011, 7 ], [ 256023, 3 ], [ 512047, 1 ], [ 1024095, 0 ], [ 2048190, 0 ], [ 4096380, 0 ], [ 8192760, 0 ], [ 16385520, 0 ] ] gap> Trajectory(a^-1,[1000,1000],15); [ [ 1000, 1000 ], [ 500, 2000 ], [ 250, 4000 ], [ 125, 8000 ], [ 62, 16001 ], [ 31, 32002 ], [ 15, 64005 ], [ 7, 128011 ], [ 3, 256023 ], [ 1, 512047 ], [ 0, 1024095 ], [ 0, 2048190 ], [ 0, 4096380 ], [ 0, 8192760 ], [ 0, 16385520 ] ]
It is left as an easy exercise to the reader to find out how the cycles of b look like.
Enter AssignGlobals(LoadRCWAExamples().ZxZ); in order to assign the global variables defined in this section.
In this section, we show how to construct finite quotients of the two infinite periodic groups introduced by Rostislav Grigorchuk in [Gri80] with the help of RCWA. The first of these, nowadays known as Grigorchuk group
, is investigated in an example given on the GAP website -- see https://www.gap-system.org/Doc/Examples/grigorchuk.html. The RCWA package permits a simpler and more elegant construction of the finite quotients of this group: The function TopElement given on the mentioned webpage gets unnecessary, and the function SequenceElement can be simplified as follows:
SequenceElement := function ( r, level )
return Permutation(Product(Filtered([1..level-1],k->k mod 3 <> r),
k->ClassTransposition( 2^(k-1)-1,2^(k+1),
2^k+2^(k-1)-1,2^(k+1))),
[0..2^level-1]);
end;
The actual constructors for the generators are modified as follows:
a := level -> Permutation(ClassTransposition(0,2,1,2),[0..2^level-1]); b := level -> SequenceElement(0,level); c := level -> SequenceElement(2,level); d := level -> SequenceElement(1,level);
All computations given on the webpage can now be done just as with the original
construction of the quotients of the Grigorchuk group. In the sequel, we construct finite quotients of the second group introduced in [Gri80]:
gap> FourCycle := RcwaMapping((4,5,6,7),[4..7]); ( 0(4), 1(4), 2(4), 3(4) ) gap> GrigorchukGroup2Generator := function ( level ) > if level = 1 then return FourCycle; else > return Restriction(FourCycle, RcwaMapping([[4,1,1]])) > * Restriction(FourCycle, RcwaMapping([[4,3,1]])) > * Restriction(GrigorchukGroup2Generator(level-1), > RcwaMapping([[4,0,1]])); > fi; > end;; gap> GrigorchukGroup2 := level -> Group(FourCycle, > GrigorchukGroup2Generator(level));;
We can do similar things as shown in the example on the GAP webpage for the first
Grigorchuk group:
gap> G := List([1..4],lev->GrigorchukGroup2(lev)); # The first 4 quotients. [ <rcwa group over Z with 2 generators>, <rcwa group over Z with 2 generators>, <rcwa group over Z with 2 generators>, <rcwa group over Z with 2 generators> ] gap> H := List([1..4],lev->Action(G[lev],[0..4^lev-1])); # Isom. perm.-gps. [ Group([ (1,2,3,4), (1,2,3,4) ]), Group([ (1,2,3,4)(5,6,7,8)(9,10,11,12)(13,14,15,16), (1,5,9,13)(2,6,10,14)(4,8,12,16) ]), <permutation group with 2 generators>, <permutation group with 2 generators> ] gap> List(H,Size); [ 4, 1024, 4294967296, 1329227995784915872903807060280344576 ] gap> List(last,n->Collected(Factors(n))); [ [ [ 2, 2 ] ], [ [ 2, 10 ] ], [ [ 2, 32 ] ], [ [ 2, 120 ] ] ] gap> List(H,NilpotencyClassOfGroup); [ 1, 6, 14, 40 ]
Enter AssignGlobals(LoadRCWAExamples().GrigorchukQuotients); in order to assign the global variables defined in this section.
The \(3n+1\) conjecture asserts that the forward orbit of any positive integer under the Collatz mapping \(T\) contains 1. In contrast, it seems likely that most
trajectories of the two mappings
diverge. However we can show by means of computation that the forward orbit of any positive integer under the action of the monoid generated by the two mappings \(T_5^-\) and \(T_5^+\) indeed contains 1. First of all, we enter the generators:
gap> T5m := RcwaMapping([[1,0,2],[5,-1,2]]);; gap> T5p := RcwaMapping([[1,0,2],[5, 1,2]]);;
We look for a number \(k\) such that for any residue class \(r(2^k)\) there is a product \(f\) of \(k\) mappings \(T_5^\pm\) whose restriction to \(r(2^k)\) is given by \(n \mapsto (an+b)/c\) where \(c>a\):
gap> k := 1;; gap> repeat > maps := List(Tuples([T5m,T5p],k),Product); > decr := List(maps,DecreasingOn); > decreasable := Union(decr); > Print(k,": "); View(decreasable); Print("\n"); > k := k + 1; > until decreasable = Integers; 1: 0(2) 2: 0(4) 3: Z \ 1(8) U 7(8) 4: 0(4) U 3(16) U 6(16) U 10(16) U 13(16) 5: Z \ 7(32) U 25(32) 6: <union of 48 residue classes (mod 64)> 7: Integers
Thus \(k=7\) serves our purposes. To be sure that for any positive integer \(n\) our monoid contains a mapping \(f\) such that \(n^f<n\), we still need to check this condition for small
\(n\). Since in case \(c>a\) we have \((an+b)/c \geq n\) if only if \(n \leq b/(c-a)\), we only need to check those \(n\) which are not larger than the largest coefficient \(b_{r(m)}\) occurring in any of the products under consideration:
gap> maxb := Maximum(List(maps,f->Maximum(List(Coefficients(f),t->t[2])))); 25999 gap> small := Filtered([1..maxb],n->ForAll(maps,f->n^f>=n)); [ 1, 7, 9, 11 ]
This means that except of 1, only for \(n \in \{{7,9,11\}}\) there is no product of 7 mappings \(T_5^\pm\) which maps \(n\) to a smaller integer. We check that also the forward orbits of these three integers contain 1 by successively computing preimages of 1:
gap> S := [1];; k := 0;; gap> repeat > S := Union(S,PreImage(T5m,S),PreImage(T5p,S)); > k := k+1; > until IsSubset(S,small); gap> k; 17
Enter AssignGlobals(LoadRCWAExamples().CollatzMapping); in order to assign the global variables defined in this section.
The free group of rank 2 embeds into RCWA(ℤ) -- in fact it embeds even in the subgroup which is generated by all class transpositions. An explicit embedding can be constructed by transferring the construction of the so-called Schottky groups
(cf. [dlH00], page 27) from PSL(2,ℂ) to RCWA(ℤ) (we use the notation from the cited book):
gap> D := AllResidueClassesModulo(4); [ 0(4), 1(4), 2(4), 3(4) ] gap> gamma1 := RepresentativeAction(RCWA(Integers), > Difference(Integers,D[1]),D[2]);; gap> gamma2 := RepresentativeAction(RCWA(Integers), > Difference(Integers,D[3]),D[4]);; gap> F2 := Group(gamma1,gamma2); <rcwa group over Z with 2 generators>
We can do some checks:
gap> X1 := Union(D{[1,2]});; X2 := Union(D{[3,4]});; gap> IsSubset(X1,X2^gamma1) and IsSubset(X1,X2^(gamma1^-1)) > and IsSubset(X2,X1^gamma2) and IsSubset(X2,X1^(gamma2^-1)); true
The generators are products of 3 class transpositions, each:
gap> Factorization(gamma1); [ ( 0(2), 1(2) ), ( 3(4), 5(8) ), ( 0(2), 1(8) ) ] gap> Factorization(gamma2); [ ( 0(2), 1(2) ), ( 1(4), 7(8) ), ( 0(2), 3(8) ) ]
The above construction is used by IsomorphismRcwaGroup (3.1-1) to embed free groups of any rank \(\geq 2\).
We give another only slightly different representation of the free group of rank 2. We verify that it really is one by applying the so-called Table-Tennis Lemma (see e.g. [dlH00], Section II.B.) to the infinite cyclic groups generated by the two generators and to the same two sets X1 and X2 as above:
gap> r1 := ClassTransposition(0,2,1,2)*ClassTransposition(0,2,1,4);; gap> r2 := ClassTransposition(0,2,1,2)*ClassTransposition(0,2,3,4);; gap> F2 := Group(r1^2,r2^2);; gap> List(GeneratorsOfGroup(F2),IsTame); [ false, false ] gap> IsSubset(X1,X2^F2.1) and IsSubset(X1,X2^(F2.1^-1)) > and IsSubset(X2,X1^F2.2) and IsSubset(X2,X1^(F2.2^-1)); true gap> [Sources(r1),Sinks(r1),Loops(r1)]; # compare with X1 [ [ 0(4) ], [ 1(4) ], [ 0(4), 1(4) ] ] gap> [Sources(r2),Sinks(r2),Loops(r2)]; # compare with X2 [ [ 2(4) ], [ 3(4) ], [ 2(4), 3(4) ] ] gap> IsSubset(X1,Union(Sinks(r1))) and IsSubset(X1,Union(Sinks(r1^-1))) > and IsSubset(X2,Union(Sinks(r2))) and IsSubset(X2,Union(Sinks(r2^-1))); true gap> IsSubset(Union(Sinks(r1)),X2^F2.1) and > IsSubset(Union(Sinks(r1^-1)),X2^(F2.1^-1)); true gap> IsSubset(Union(Sinks(r2)),X1^F2.2) and > IsSubset(Union(Sinks(r2^-1)),X1^(F2.2^-1)); true
Drawing the transition graphs of r1 and r2 for modulus 4 may help to understand what is actually done in this calculation. It is easy to see that the group generated by r1 and r2 is not free:
gap> Order(r1/r2); 3
The modular group PSL(2,ℤ) embeds into CT(ℤ) as well. We give an embedding, and check that it really is one by applying the Table Tennis Lemma as above:
gap> PSL2Z := > Group(ClassTransposition(0,3,1,3) * ClassTransposition(0,3,2,3), > ClassTransposition(1,3,0,6) * ClassTransposition(2,3,3,6));; gap> List(GeneratorsOfGroup(PSL2Z),Order); [ 3, 2 ] gap> X1 := Difference(Integers,ResidueClass(0,3)); Z \ 0(3) gap> X2 := ResidueClass(0,3); 0(3) gap> IsSubset(X1,X2^PSL2Z.1) and IsSubset(X1,X2^(PSL2Z.1^2)); true gap> IsSubset(X2,X1^PSL2Z.2); true
A slightly different representation of PSL(2,ℤ) can be obtained by using RCWA's general method for IsomorphismRcwaGroup for free products of finite groups:
gap> G := Image(IsomorphismRcwaGroup(FreeProduct(CyclicGroup(3), > CyclicGroup(2)))); <wild rcwa group over Z with 2 generators> gap> List(GeneratorsOfGroup(G),Factorization); [ [ ( 0(4), 2(4) ), ( 1(2), 0(4) ) ], [ ( 0(2), 1(2) ) ] ]
Enter AssignGlobals(LoadRCWAExamples().F2_PSL2Z); in order to assign the global variables defined in this section.
generated by GAPDoc2HTML